图像平滑与锐化技巧

在介绍图像平滑（去噪声）和锐化之前，首先介绍一下模板操作。

模板操作是数字图像处理中常用的运算方法，图像的平滑、锐化以及后面将要介绍的细化、边缘检测都要用到模板操作。

对于最简单的局部平滑算法，即非加权领域平均，它均等地对待领域中的每个像素。设图像中某像素灰度值为f（x，y），它的领域S为N×N，点集的总数为M，则平滑后这点的灰度值为

对于这样的操作，可以用模板操作来表示。为了叙述方便，设N=3，则可以用如下的表示方法来表示此操作：

这种表示方法有点像矩阵，称其为模板（Template）。中间的黑点表示该元素为中心元素，即该元素是要进行处理的元素。如果模板是

则该操作应该描述为：将原图中一个像素的灰度值和它右下邻近的8个像素的灰度值相加，然后将求得的平均值（除以9）作为新图中该像素的灰度值。

如果模板为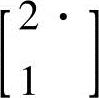，则表示将自身灰度值的2倍加下边的元素灰度值作为新值，而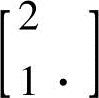则表示将自身灰度值加上边元素灰度值的2倍作为新灰度值。

通常模板不允许移出边界，所以处理后的新图像会比原图小。例如：当模板是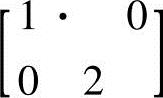，原图灰度值矩阵是时，经过模板操作后的图像为，“—”表示边界上无法进行模板操作的点，一般的做法是复制原图的灰度值，不再进行任何其他的处理。

模板操作实现了一种邻域运算（Neighborhood Operation），即某个像素点的结果不仅和本像素灰度有关，而且和领域点的值有关。模板运算在数学中的描述是卷积（或互相关）运算，在这里就不再介绍了，有兴趣的读者可以自行查看相应的数学书籍。

模板运算在图像处理中经常要用到，但是当图像很大时，运算量是非常可观的，也非常耗时。以模板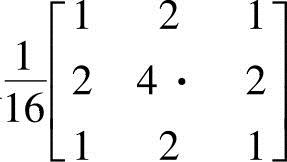运算为例，每个像素完成一次模板操作要用9次乘法、8次加法和1次除法。对于一幅N×N（宽度×高度）的图像，就是要进行9（N-2）2次乘法、8（N-2）2次加法和（N-2）2次除法操作，算法复杂度为O（N²），这对于大图像来说，是非常可怕的，所以常用的模板并不大，如3×3、4×4。有很多专用的图像处理系统，用硬件来完成模板运算，大大提高了速度。

另外，可以设法将二维模板运算转换成一维模板运算，这对速度的提高也是有益的。例如，上面的例子可以分解成一个水平模板和一个竖直模板，即

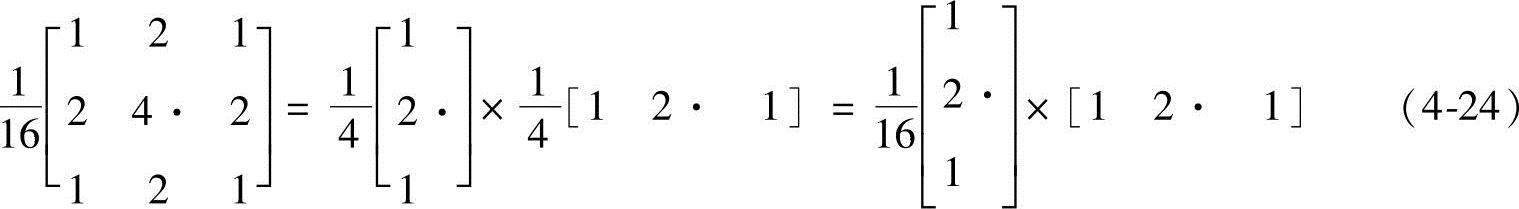
这样，改进后将要进行的是6（N-2）（N-1）次乘法，4（N-2）（N-1）次加法和（N-2）²次除法操作，减少了不少次乘法和加法运算。

下面来具体验证一下该分解算法的可行性，设图像为，直接经过模板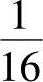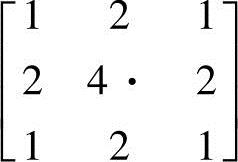处理后变为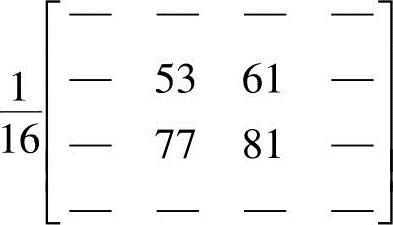。但是如果采用分解后的模板来处理，结果为

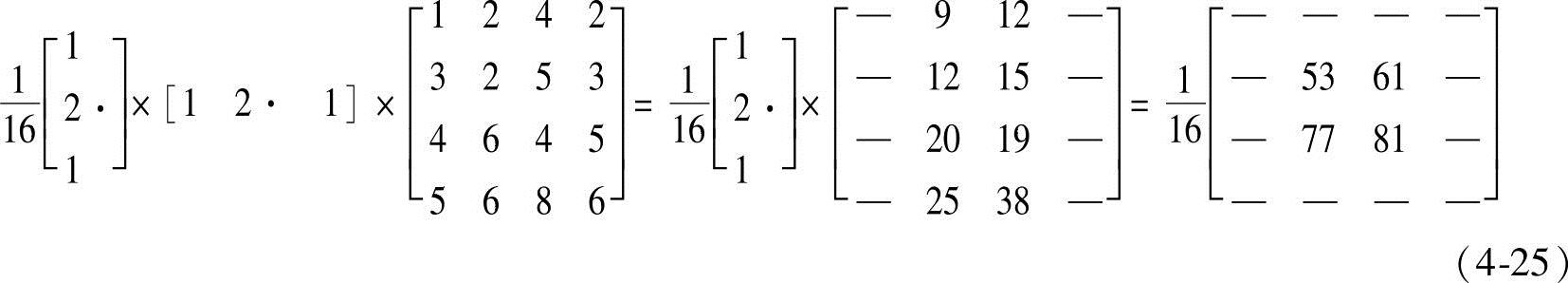
可以发现，两种计算方法得出的结果是完全相同的。

1.图像的平滑

图像在生成和传输过程中常受到各种噪声的干扰和影响，使图像质量下降。为了抑制噪声以改善图像质量，必须对图像进行平滑处理，这可在空域或频域中进行。在平滑噪声时应尽量不损害图像中边沿和各种细节。

对于滤除图像中的噪声，人们已经提出了很多方法。通常，将数字图像的平滑技术分化为两类：一类是全局处理，即对噪声图像的整体或大的块进行校正，以得到平滑的图像，但对大多数图像而言，人们不知道或不可能用简单的随机过程精确地描述统计模型，而且这些技术计算量也是相当大的；另一类平滑技术是对噪声图像使用局部算子，当对某一像素进行平滑处理时，仅对它的局部小领域的一些像素加以运算，其优点是计算效率高，而且可以对多个像素并行处理，因此可实现实时或准实时处理。

平滑模板的思想是通过一点和周围几个点的运算（通常为平均运算）来去除突然变化的点，从而滤掉一定的噪声，但图像有一定程度的模糊。而减少图像模糊代价是图像平滑研究的主要问题之一。这主要取决于噪声本身的特性。一般情况下，通过选择不同的模板来消除不同的噪声。常用的模板有

其中，最后一个模板又常称为高斯模板，它是通过采样二维高斯函数得到的。

2.图像的锐化

图像锐化处理的目的是使模糊的图像变得更加清晰起来。通常针对引起图像模糊的原因而进行相应的锐化操作，属于图像复原的内容，在这里只是介绍一般的去模糊算法。

图像的模糊实质上就是图像受到平均或积分运算造成的，因此可以对图像进行逆运算如微分运算来使图像清晰化。从频谱角度来分析，图像模糊的实质是其高频分量被衰减，因而可以通过高通滤波操作来清晰图像。但要注意，能够迸行锐化处理的图像必须有较高的信噪比，否则锐化后图像信噪比反而更低，从而使噪声的增加比信号的增加还要多，因此一般是先去除或减轻噪声后再进行锐化处理。

图像锐化一般有两种方法：一种是微分法；另外一种是高通滤波法。后者的工作原理和低通滤波相似，这里就不再详细介绍了。下面主要介绍一下两种常用的微分锐化方法：梯度锐化和拉普拉斯锐化。对于高通滤波法，只给出几种常用的高通滤波器。

（1）梯度锐化 图像的模糊相当于图像被平均或被积分。为实现图像的锐化，必须用它的反运算“微分”，来加强高频分量的作用，从而使图像轮廓清晰。由于模糊图像的特征（如边沿的走向等）各不相同，要进行锐化，应该采用各向同性、具有旋转不变的线性微分算子。

图像处理中最常用的微分方法是求梯度。图像f（x，y）所在的梯度是一个向量，定义为

梯度有两个重要性质：

1）梯度的方向在函数f（x，y）最大变化率方向上；

2）梯度的幅度用GM[f（x，y）]表示，其值为

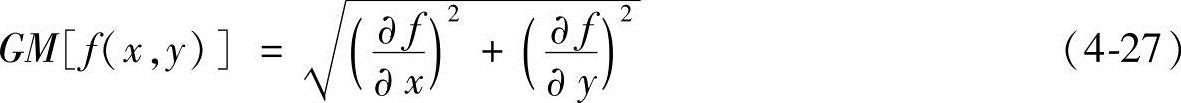
点（x，y）梯度的幅度为梯度的模，即

GM（x，y）={[f（x，y）-f（x+1），y]²+[f（x，y）-f（x，y+1）]²}^1/2 （4-28）

为了运算简便，可以简化为

GM（x，y）≈f（x，y）-f（x+1），y+f（x，y）-f（x，y+1）（4-29）

或利用Roberts梯度算子

GM（x，y）={[f（x，y）-f（x+1，y+1）]²+[f（x+1，y）-f（x，y+1）]²}^1/2 （4-30）

Roberts算子也可以简化为

GM（x，y）=f（x，y）-f（x+1，y+1）+f（x+1，y）-f（x，y+1） （4-31）

梯度算子一旦算出后，就可以根据不同的需要生成不同的梯度增强图像。

此方法的缺点是增强图像仅仅显示灰度变换比较陡峭的边沿轮廓，而灰度变化比较平缓或者比较均匀的地方则呈现黑色。

人们又提出了一些改进的方法，例如：

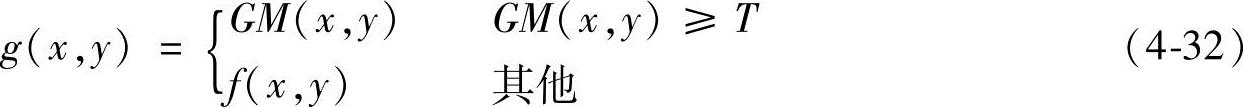
式中，T是一个非负的阈值。适当地选取T，即可使明显的边沿轮廓得到突出，并且不会破坏原来灰度变换比较平缓的背景。

还有一些其他方法，例如将梯度幅度大于阈值的设置为某个指定的灰度或者梯度幅度，梯度幅度小于阈值的像素则设置为某个指定灰度或者梯度幅度等，这里就不一一介绍了，读者可以参考数字图像处理文献。(www.xing528.com)

（2）拉普拉斯锐化 拉普拉斯锐化运算也是偏导数运算的线性组合，而且是一种各向同性（旋转不变性）的线性运算。设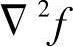为拉普拉斯算子，则

对于离散数字图像f（i，j），其一阶偏导数为

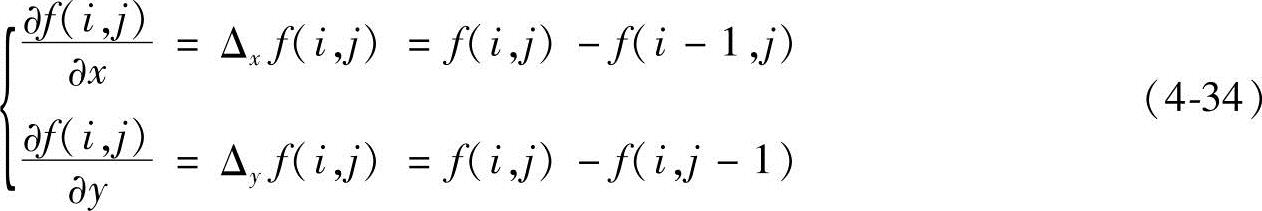
其二阶偏导数为

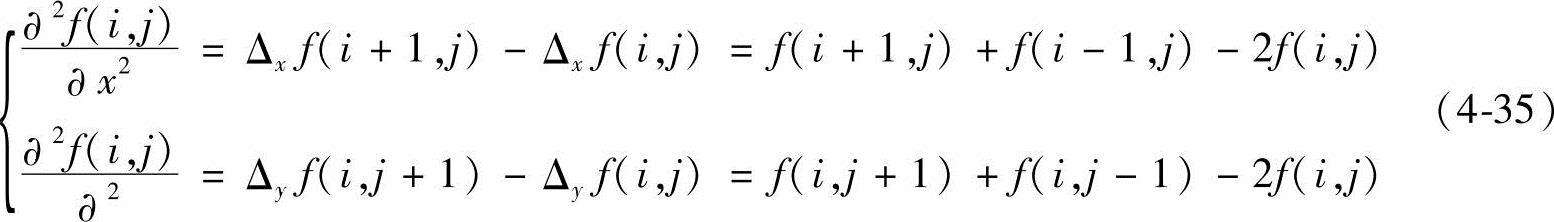
所以，拉普拉斯算子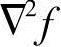为

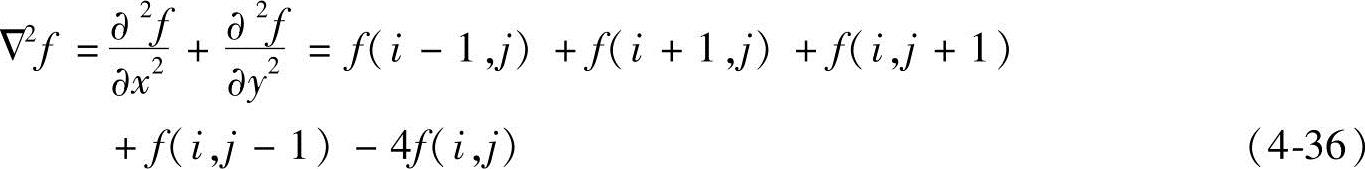
对于扩散现象引起的图像模糊，可以用下式来进行锐化：

图3-1 FACS把脸部运动分解为肌肉运动

式中，kτ是与扩散效应有关的系数。该系数取值要合理，如果kτ过大，图像轮廓边缘会产生过冲；反之如果kτ过小，锐化效果就不明显。

如果令kτ=1，则变换公式为

g（i，j）=5f（i，j）-f（i-1，j）-f（i+1，j）-f（i，j+1）-f（i，j-1） （4-38）

用模板表示如下：

这样拉普拉斯锐化运算完全可以转换成模板运算。其实常用的拉普拉斯锐化模板还有另外一种形式：

拉普拉斯算子有两个缺点：一是边沿的方向被丢失；另一个是拉普拉斯算子为二阶差分，双倍加强了图中的噪声影响。优点是各向同性，即旋转不变。

（3）高通滤波器 由于图像中的边缘及急剧变化部分与图像高频分量有关，因此利用高通滤波器衰减图像信号中的低频部分，能相对增强图像高频部分，从而实现图像锐化的目的。常用的高通滤波器有理想高通滤波器、巴特沃夫高通滤波器、指数高通滤波器和梯形高通滤波器。下面将分别给出各种高通滤波器的转移函数。

1）理想高通滤波器 理想二维高通滤波器的传递函数如下：

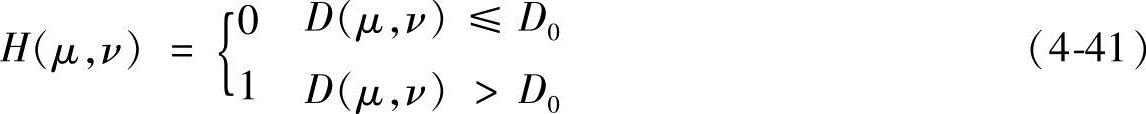
式中，D₀是从频率平面原点算起的截止频率（或截止距离）。D（μ，ν）为

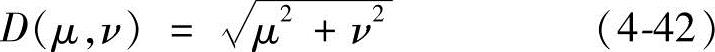
理想高通滤波器传递函数的径向剖面如图4-9所示。

理想高通滤波器和理想低通滤波器相反，它正好将以D₀为半径的圆内的频率成分（低频部分）衰减掉，而对圆外的频率成分（高频部分）则可以无损通过。

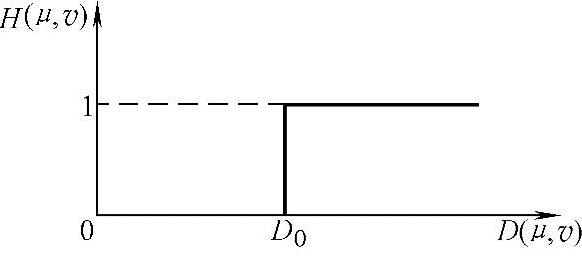
图4-9 理想高通滤波器传递函数径向剖面

2）巴特沃夫高通滤波器 截止频率为D₀的n阶巴特沃夫高通滤波器的传递函数如下所示：

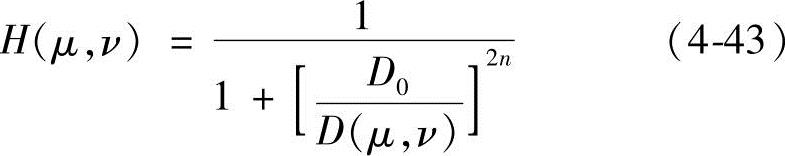
式中，D（μ，ν）仍然为。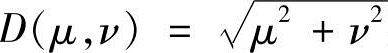

巴特沃夫高通滤波器传递函数径向剖面如图4-10所示。

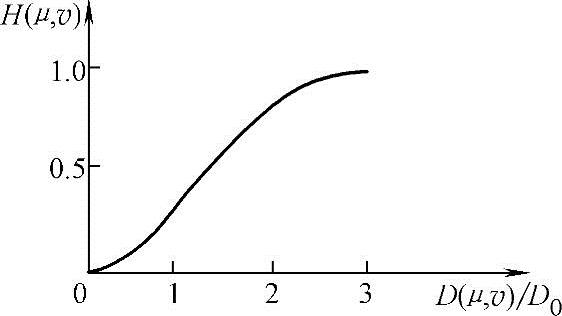
图4-10 巴特沃夫高通滤波 器传递函数径向剖面

和低通滤波器类似，定义H（μ，ν）下降到其最大值一半处的D（μ，ν）为截止频率点D₀。一般情况下，高通滤波器的截止频率选择使H（μ，ν）下降到其最大值的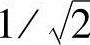处，满足该条件的传递函数可以修改为

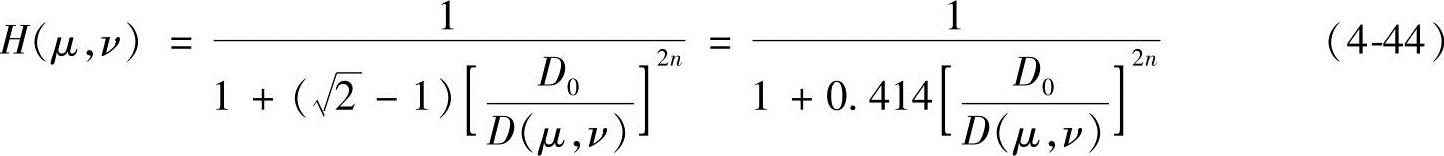
3）指数高通滤波器 截止频率为D₀的指数高通滤波器的传递函数如下所示：

式中，D₀为截止频率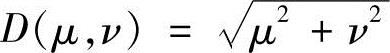；。参数n控制着H（μ，ν）的增长率。指数高通滤波器的传递函数径向剖面如图4-11所示。

当D（μ，ν）=D₀时，H（μ，ν）=1/e，如果仍然把截止频率定在H（μ，ν）最大值的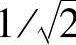处，则传递函数可以修改为如下形式：

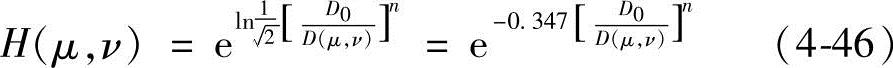
4）梯形高通滤波器 梯形高通滤波器的传递函数可以用下式表示：

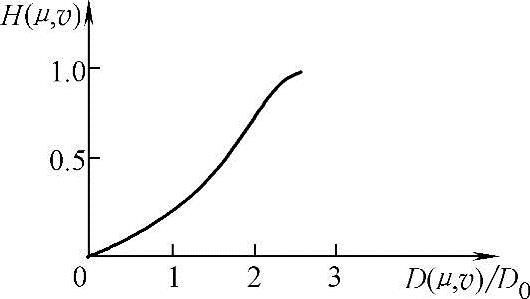
图4-11 指数高通滤波器传递函数径向剖面

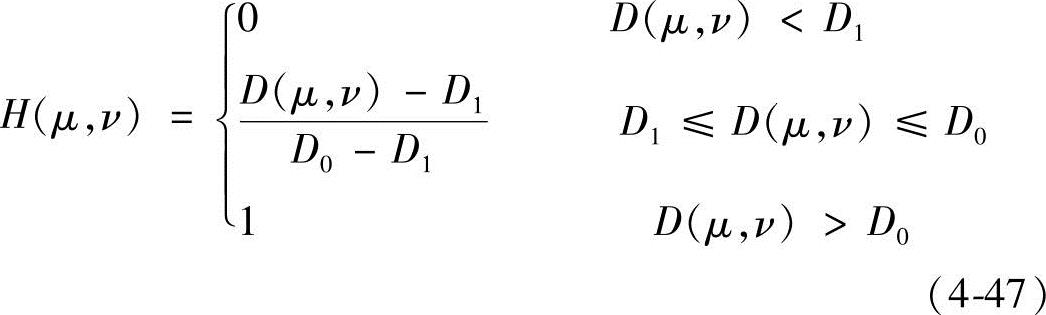
同样，式中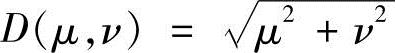。D₀和D₁为指定值，并且D₀＞D₁，定义截止频率为D₀，D₁是任意选的，只要满足D₀＞D₁即可。梯形高通滤波器的传递函数径向剖面如图4-12所示。

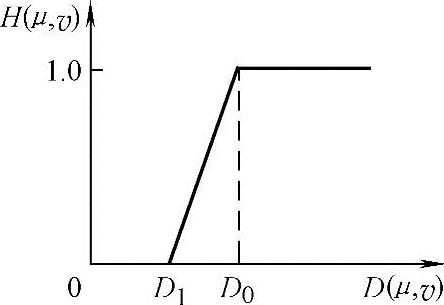
图4-12 梯度高通滤波器传递函数径向剖面