集电线路的直击雷过电压的介绍

雷直击集电线路有3种情况：雷击塔顶或其附近的避雷线（统称雷击塔顶）；雷击避雷线挡距中央；雷绕过避雷线而击于导线，也称为绕击。3种情况如图4-21所示。

图4-21　雷直击集电线路的3种类型　

图4-22　雷击塔顶时的等效电路图

4.3.2.1　有避雷线时的直击雷过电压

1.雷击塔顶

雷击塔顶时，大部分电流通过被击杆塔流入大地，巨大的雷电流会在杆塔和接地电阻上产生很高的电位，使电位原来为零的杆塔变为高电位，对线路放电，从而造成闪络，即反击。对于有避雷线的线路，其等效电图如图4-22所示。

雷击时，绝大部分雷电流流经被击杆塔入地，小部分雷电流则通过避雷线从相邻的杆塔入地。流经被击杆塔入地的电流igt与总电流i的关系为

式中　βg——分流系数，它的值小于1。

杆塔塔顶电位ugt为

式中　Rch——杆塔冲击接地电阻，Ω；

Lgt——杆塔总电感，μH。

由式（4-5）和式（4-6）可得

以雷电流的波前陡度为平均陡度，即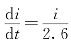，并取雷电流幅值I为雷电流i，则可得到塔顶的电位ugt为

由于避雷线与塔顶相连，则避雷线也具有相同的电位ugt，避雷线与导线之间存在耦合关系，并且极性与雷电流相同，则绝缘子串在这一部分的电压值为

若计及导线上的感应雷过电压，可通过式子U′=U-KcU=（1-Kc）U求得

将式（4-9）和式（4-10）叠加可得作用在绝缘子串上的电压Uj为

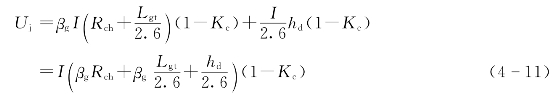
若Uj超过绝缘子串50%冲击放电电压，绝缘子串将会发生闪络，则雷击塔顶的耐雷水平I为

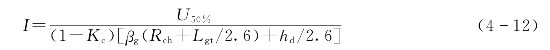
因为从杆塔流入大地的雷电流多为负极性，此时导线相对于杆塔来说是正极性的，所以U50%应取绝缘子串的正极性50%冲击放电电压。

2.雷击避雷线挡距中央的过电压及其空气间隙

（1）雷击点的过电压。避雷线挡距中央遭受雷击时如图4-23所示，根据彼得逊法则可以画出它的等值电路图，如图4-24所示。则雷击点的电压uA为

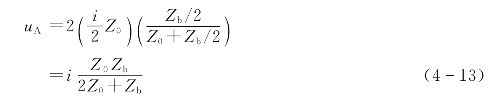
式中　i——雷电流。

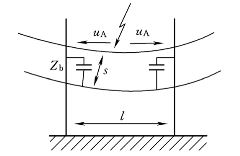
图4-23　雷击避雷线挡距中央示意图

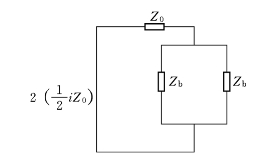
图4-24　雷击避雷线挡距中央等效电路图

在计算中可以近似地取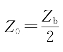，代入式（4-13）可得

（2）避雷线与导线之间的空气间隙s上所能承受的最大电压。若雷电流取斜角波，即i=αt，则有(www.xing528.com)

由式（4-15）可以看出，雷击点处的电压将随着时间的增加而增加。同时，这一电压波沿着两侧避雷线向相邻杆塔传播，经过0.5l/v（l为挡距长度，v为波速）到达杆塔。根据行波传播规则，在杆塔处将发生负反射，负的电压波沿避雷线经过相同的时间传回雷击点后，雷击点的电压uA将不再升高，雷电压达到最大值，即

由于避雷线与导线间存在耦合作用，在导线上将产生耦合电压KcuA，因此雷击处避雷线与导线间的空气间隙上所能承受的最大电压US为

由式（4-17）可知，雷击避雷线挡距中央时，雷击处避雷线与空气间隙间的最大电压US与挡距长度l成正比。因此，保证避雷线与导线之间有足够的距离可以防止该空气间隙被击穿。

根据理论分析和运行经验，我国相关规程规定挡距中央导线、地线之间的空气间隙s（m）的经验公式为

电力系统多年运行经验表明，按式（4-18）求得的s足以满足避雷线与导线之间不发生闪络的要求。

3.绕击时导线的过电压及耐雷水平

绕击的情况相当于在导线上方未架设避雷线的情况下雷电直击导线。此时雷电流沿着导线向两侧流动。假设Z0为雷电通道的波阻抗，Z/2为雷击点两侧导线的并联波阻抗，可建立等效电路如图4-25所示。

若计及在过电压情况下冲击电晕的影响，Z可取值为400Ω，则雷击点A的电压UA为

图4-25　绕击时等效电路图

当UA超过绝缘子串的50%冲击闪络电压时将发生闪络，从而可得导线的绕击耐雷水平为

4.3.2.2　无避雷线时的直击雷过电压

集电线路未架设避雷线时，雷击线路有两种情况：一是雷直击导线；二是雷击塔顶。

1.雷直击导线

由绕击情况可得，雷直击导线时雷击点的电压为UA=100I，则耐雷水平为

2.雷击塔顶

雷直击塔顶时，无雷电流分流的影响，所有的雷电流I均通过接地电阻流入大地。设杆塔的电感为Lgt，雷电流波头为2.6μs，则α=I/2.6，可得等效电路如图4-26所示。

此时，塔顶电位为

导线上的感应过电压为

由于感应过电压极性与塔顶电位极性相反，则作用于绝缘子串上的电压为

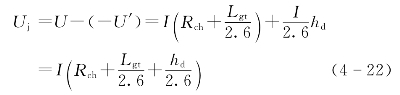
线路的耐雷水平为

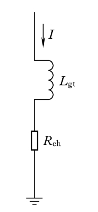
图4-26　无避雷线时雷击塔顶时的等效电路图

雷击塔顶时，若雷电流幅值超过线路的耐雷水平，会致使塔顶对一相导线放电。由于工频电流较小，不能形成稳定的工频电弧，因此不会引起线路跳闸故障。若第一相闪络后，再向第二相反击，此时两相间绝缘子串闪络出现大的短路电流，会引起线路跳闸。

当第一相闪络后，可认为该导线具有与塔顶一样的电位。第一相与第二相导线之间有耦合作用，则两相间的电压差为

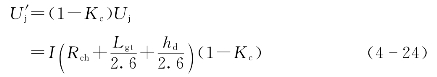
线路的耐雷水平为