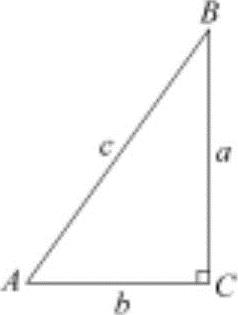
图1-1 直角三角形
1.三角函数的定义
在直角三角形ABC(图1-1)中,如果知道了两条边,就可以知道锐角A或B的大小。同样,如果知道了一条边和一个锐角,也就可以求出另外两条边的大小。
把三角形的BC边长用a表示,AC边长用b表示,AB边长用c表示,按下面定义就可得出常用的四个公式:
1)锐角A所对的直角边a与斜边c的比,称为锐角A的正弦,即
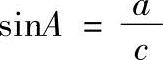
2)锐角A相邻的直角边b与斜边c的比,称为锐角A的余弦,即
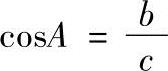
3)锐角A所对的直角边a与此角相邻的直角边b的比,称为锐角A的正切,即
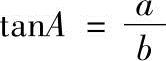
4)锐角A相邻的直角边b与此角所对的直角边a的比,称为锐角A的余切,即
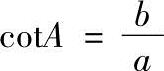
同样,锐角B有
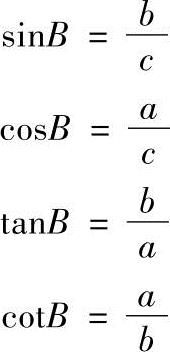
由以上的关系可知
sinA=cosB
cosA=sinB
tanA=cotB
cotA=tanB
从四个定义中可得
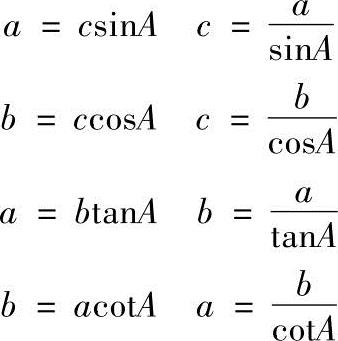
2.勾股定理
在直角三角形中,斜边的平方等于两条直角边的平方和,即
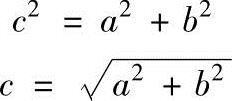
同样,可以把上面公式变为
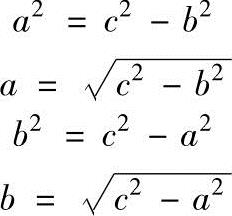
在直角三角形中,如果知道了两条边的长度,就可以应用勾股定理求出第三条边的长度。
例 b=12mm,a=10mm,求c。
解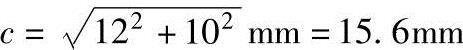
例 c=20mm,b=12mm,求a。
解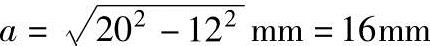
3.30°、45°、60°的三角函数值(https://www.xing528.com)
30°、45°、60°的三角函数值,可以用数学方法求出,不需要查三角函数表。
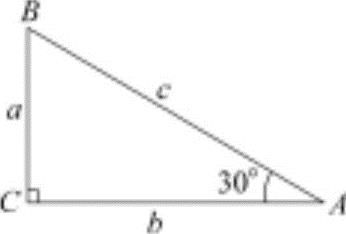
图1-2 30°直角三角形
1)30°的函数值。在直角三角形ABC中(图1-2),A=30°,根据几何定理,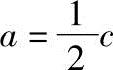 ,所以
,所以
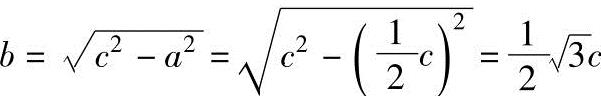
因而
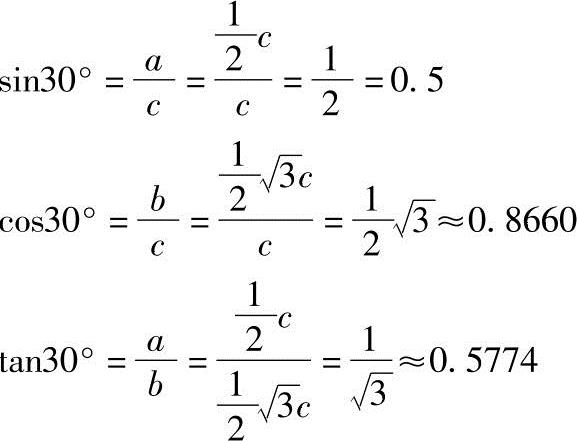
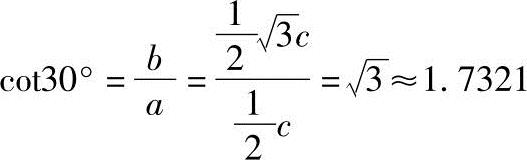
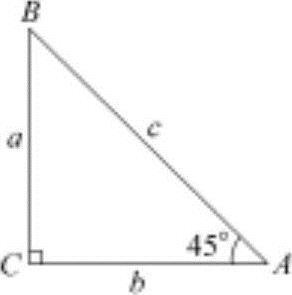
图1-3 45°直角三角形
2)45°的三角函数值。在直角三角形ABC(图1-3)中,A=45°,b=a,所以
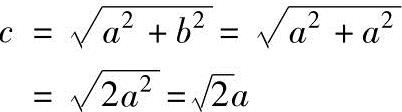
因而
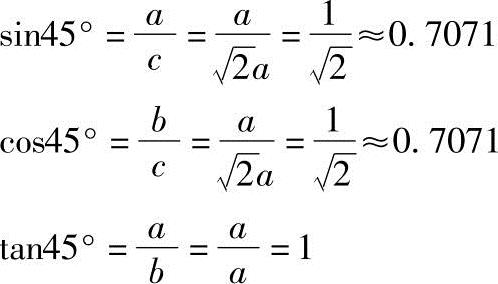
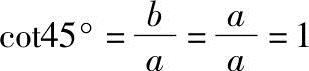
3)60°的三角函数值。在直角三角形ABC(图1-4)中,A=60°,按几何定理,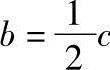 ,所以
,所以
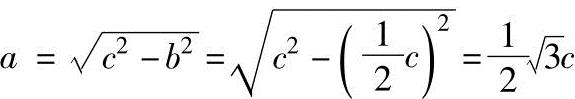
因而
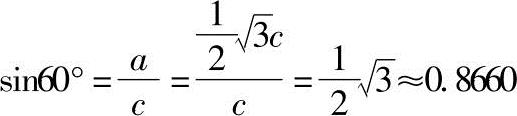
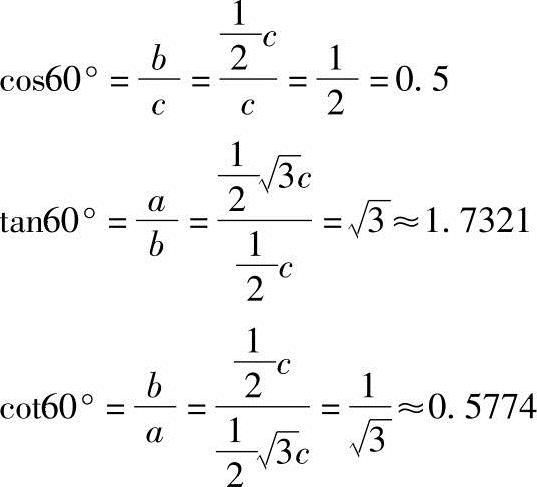
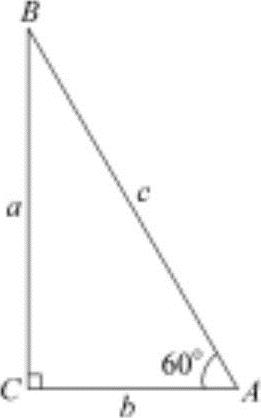
图1-4 60°直角三角形
4.常用公式
(1)同角三角函数间的关系
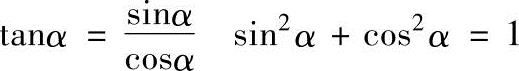
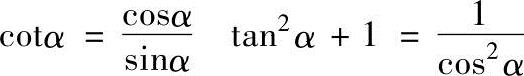
(2)诱导公式(表1-1)
表1-1 诱导公式
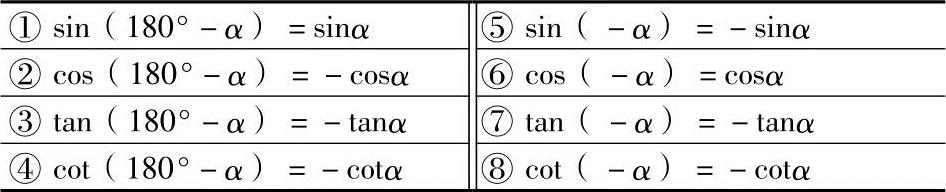
(3)两角和、两角差、倍角和半角的三角函数
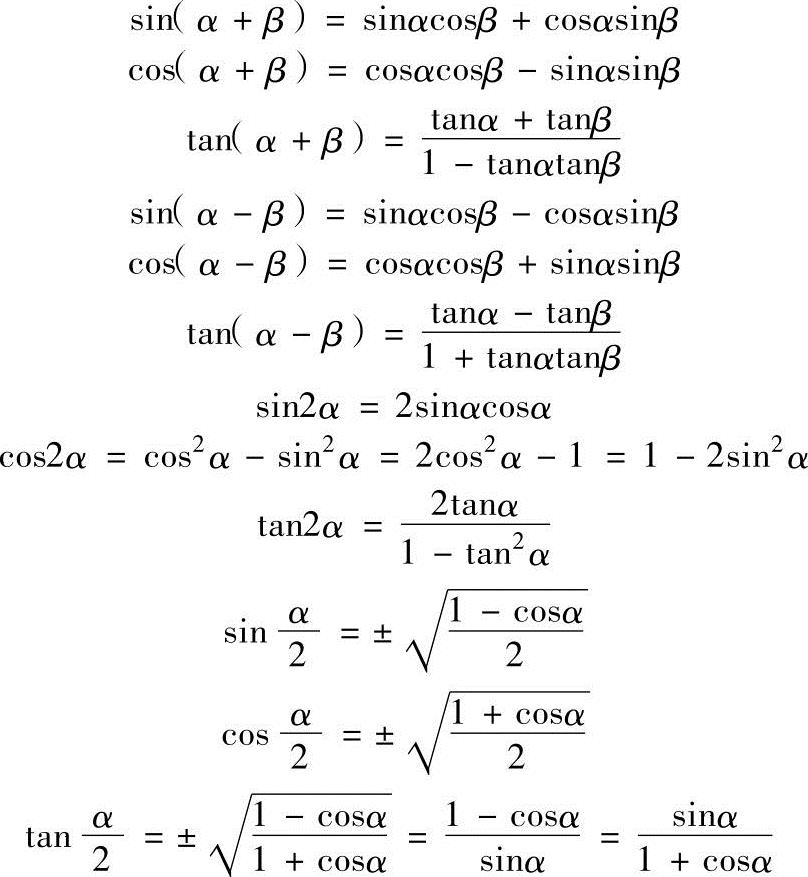
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




