聚合物共混物性能与单组分性能的关系式探究

影响共混物性能的因素，首先是各共混物组分的性能。共混物的性能与单一组分的性能之间，都存在某种关联。以双组分共混体系为例，若设共混物性能为P，如密度、电性能、黏度、热性能、力学性能、玻璃态转变温度等；组分1性能为P1，组分2性能为P2，则可建立P与P1、P2之间的关系式。

共混物的性能还与共混物的形态密切相关。对于不同形态的共混物之间的关系式也是不大相同的。

（一）简单关系式

对于共混物性能P与单一组分性能P1、P2之间的关系，若不考虑共混物形态的因素，则可以建立一些较为简单的关系式，最常用的有如下两个关系式：

式中：φ1、φ2为组分1与组分2的体积分数。在式中共混物性能只是组分1与组分2性能的算术加和。

采用以上两式表征共混物性能P与单一组分性能P1、P2之间的关系，由于未考虑共混物的形态因素，因而与实际共混物的性能会有较大的偏差。为了更好地反映共混物性能与单一组分性能之间的关系，应根据不同的共混物形态，分别建立相应的关系式。

（二）均相共混体系

均相体系共混物性能与单一组分性能之间的关系式，可在上式的基础上加以改进而获得。对于大多数共混物而言，各组分之间通常是有相互作用的。因而，均相体系共混物性能可以用下式表征：

式中：I是两组分之间的相互作用参数，根据两组分之间相互作用的具体情况，可取正值或负值。若I值为0，则与式（3－8）相同。

（三）海—岛结构两相体系

影响海—岛结构两相体系性能的因素，较之均相体系要复杂得多。Nielsen提出了海—岛结构两相体系性能与单一组分性能及结构形态因素的关系式。由于海—岛结构两相体系在形态上的复杂性，这些关系式也远较均相体系的关系式复杂。按Nielsen的混合法则，若两相体系中的分散相为硬组分，而连续相为软组分（这一设定主要适用于填充体系，或塑料增强橡胶的体系），则两相体系性能与单一组分性能及结构形态因素的关系如式（3－11）所示：

式中：P——共混物的性能；

P1——两相体系中连续相的性能；

φ2——分散相体系的体积分数；

A、B、ψ——均为参数。

其中：

式中：KE为爱因斯坦系数，是一个与分散相颗粒的形状、取向、界面结合等因素有关的系数。对于共混物的不同性能，有不同的爱因斯坦系数（如力学性能的爱因斯坦系数、电学性能的爱因斯坦系数）。在某些情况下（如分散相粒子的形状较为规整时），KE可由理论计算得到；而在另一些情况下，KE值需根据实验数据推得。某些体系的力学性能的爱因斯坦系数KE如表3－6所示。

表3－6　力学性能的爱因斯坦系数KE

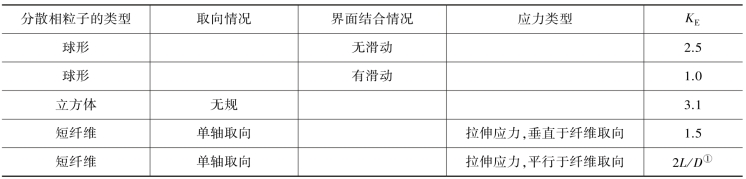
①L／D为纤维长径比。

B是取决于各组分性能及KE（体现在A值中）的参数：(https://www.xing528.com)

式中：P2——分散相的性能。

ψ为对比浓度，是最大堆砌密度φm的函数：

引入这个φm因子的前提，是假想将分散相粒子以某种形式“堆砌”起来，“堆砌”的形式取决于分散相粒子在共混物中的具体情况，与分散相粒子的形状、粒子的排布方式（有规、无规、是否聚结）、粒子的粒径分布等有关。换言之，φm是分散相粒子在某一种特定的存在状况下可能达到的最大相对密度。因此，将φm命名为最大堆砌密度。φm这一因子所反映的正是分散相粒子的某一种特定的存在状况的空间特征。若干种不同“存在状况”的分散相粒子的φm值见表3－7。

表3－7　最大堆砌密度φm

式（3－11）中所反映的是分散相为“硬组分”，而连续相为“软组分”时，共混物性能与纯组分性能的关系。如果分散相为“软组分”，而连续相为“硬组分”，譬如橡胶增韧塑料体系，则式（3－11）应改为：

式中：

其余符号的含义与式（3－11）相同。

（四）海—海结构两相体系

采用机械共混法，也可在一定条件下获得具有两相连续的海—海结构的两相体系。海—海结构两相体系，包括聚合物互穿网络（IPN）、许多嵌段共聚物等。对于海—海结构两相体系，共混物性能与单组分性能之间，可以有如下关系式：

式中：φ1——组分1的体积分数；

φ2——组分2的体积分数；

n——与体系有关的参数（－1＜n＜1）。

以结晶聚合物为例，结晶聚合物可以看作是晶相与非晶相的两相体系，且两相都是连续的。一些结晶聚合物（如PE、PP、尼龙）的剪切模量可满足下式（取n＝0.2）：

式中：G——结晶聚合物样品的剪切模量；

G1——晶相的剪切模量；

G2——非晶相的剪切模量；

φ1，φ2——分别为晶相与非晶相的体积分数。

以上分别介绍了均相体系、海—岛结构两相体系及海—海结构两相体系的性能与纯组分性能的若干关系式。这些关系式对于探讨共混物的性能具有一定的指导意义。对于具体的共混体系，可以根据体系的特点，建立相应的关系式。