上游离心泵的特点和应用场景

离心泵作为输水管道的上游边界条件时，需要考虑启泵、稳定运行、停泵这三种工况。

（1）启泵工况

离心泵启动后，转速N从0增大到额定转速N n，在转速逐渐增大的期间由泵的相似理论可得

令无因次转速可得在转速为任意转速N时水泵的性能曲线

式中：H sh——额定转速下对应的水头值。

联立式（5.29）和相容性方程式（5.36）可得

设T S为水泵启动所需的总时间，在这期间β从0变为1，任意时刻β=Q P1可由式（5.50）求出，再将Q P1代入式（5.49）即可求解出H P1。

（2）稳定运行工况

离心泵处于稳定运行工况时，可用抛物线公式近似表示水头与流量之间的关系，即

式中：H P1——水泵出口截面在流量为零时刻对应的压力值，m；

a 1、a 2——拟合性能曲线的常数。

联立式（5.51）与相容性方程式（5.37）可得

在计算得到Q P1之后，将其代入式（5.51）即可求得H P1。

（3）停泵工况

离心泵在停泵工况中的水泵边界方程有三种，分别是水泵全特性方程、水泵水头平衡方程和水泵机组惯性方程[3]。

离心泵的全特性曲线经过Marchel等人的改造[4]得到

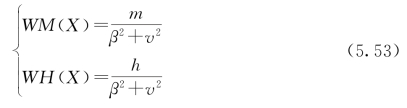(www.xing528.com)

式中：

图5.4为输水管道上的离心泵示意图。

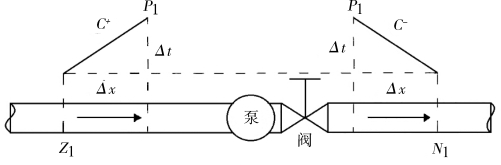
图5.4　离心泵的上下游水头平衡边界条件示意图

在停泵的整个过程中，稳态下的水头平衡方程仍然成立，即

式中：H Z——水泵入口端压力水头，m；

H——水泵工作扬程，m；

H f——阀门水头损失，m；

H N——水泵出口端压力水头，m。

其中H o是阀门在完全开启时的水头损失。

联立式（5.54）和水泵入口前端管道的相容性方程可得水泵在停泵时的水头平衡方程：

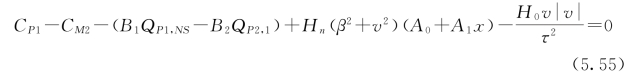
由动量定理可得，作用在水泵机组转子上合力矩与转子转速的变化率成正比，即

式中：GD 2——水泵的转动惯量，kg·m2；

g——重力加速度，m/s2；

M——作用在水泵机组上的合力矩，N·m；

W——水泵旋转角速度，ω/s。

水泵转速变化方程式可由式（5.56）得到：

联立式（5.54）和式（5.57）即可求出β和v的值，再联立相容性方程式（5.23）和式（5.24）即可求解。