液力元件的相似原理及其应用

相似原理是液力元件进行基型设计，通过模型或基准型实验来确定实物或系列化产品性能的理论基础。在基型设计过程中，循环圆形状、叶轮布置、叶片形状和数目以及各种计算参数往往基于模型或基准型选取，几何尺寸则依据相似原理加以确定。

如果要保证液力元件的模型或基准型，与几何尺寸缩放后的实物具有相同的性能，必须保证两液力元件满足3个相似条件：几何相似、运动相似和动力相似。

几何相似指两液力元件的过流部分（流道和循环圆）几何形状相似，相应各线性尺寸成比例，相应各角度相等。

运动相似指在流道对应位置上，液体质点在相同的速比工况下的速度三角形相似，即相应位置上速度成比例，速度夹角相等。液力元件运动相似的工况也称为等倾角工况。

动力相似指在流道对应位置上，液体质点上作用着同样性质的力，并且每类作用力的方向相同，力的大小成比例。

实际上，要使两个液力元件作用在液流相应点的所有的力（重力、黏性力、惯性力、表面张力、压力等）都成比例是不可能的。但是，在一般情况下，总可以把这些力的作用影响分为主要的和次要的。仅保证主要的力符合动力相似准则，称为部分动力相似。在液力元件中，主要保证惯性力和黏性力相似的部分动力相似，即要求保证雷诺数相等。

在几何相似、运动相似和动力相似三者中，几何相似是基础。没有几何相似，就不可能有运动相似和动力相似。运动相似和动力相似是互为条件相依存在的。

根据相似理论，可以推导出相似的液力元件其流量、能头、力矩和功率的有关定律。在推导过程中，需要对一些物理量进行量纲分析和计算，如果令T表示时间、L表示长度、M表示质量，则各流动参数的量纲可以进行如下表述（表12.6.1）。

表12.6.1　基本物理单位量纲

设有两个相似的液力元件，其中一个为模型液力元件，以下标m表示其有关参数；另一个为实物液力元件，以下标s表示其有关参数。根据几何相似和动力相似，各种线性尺寸和速度间存在如下的比例关系：

第一相似定律：它表示几何相似的液力元件，在等倾角工况下，其体积流量与转速和几何尺寸的关系。

因为液力元件循环圆中的流量为Q=2πRbψvm，其中b为流道宽度，ψ为流道阻塞系数，则有

代入

由量纲分析，可得(www.xing528.com)

式（12.6.1）即为第一相似定律的表达式。它说明两个相似的液力元件的体积流量之比与有效直径比值的三次方和泵轮转速比值的一次方成正比，即与体积流量量纲L3T-1一致。

第二相似定律：它表示几何相似的液力元件，在等倾角工况下，其能头与转速和几何尺寸之间的关系。

由欧拉方程可知

则

由量纲分析，可得

式（12.6.2）即为第二相似定律的表达式，它说明了相似的液力元件的能头之比与有效直径比的平方和泵轮转速比的平方成正比，即与能头量纲L2T-2一致。

第三相似定律：它表示几何相似的液力元件，在等倾角工况下，其功率与密度、转速和几何尺寸之间的关系。

液力元件的功率

则代入第一和第二相似定律，有

式（12.6.3）表明，两几何相似的液力元件，在等倾角工况下，其功率比值，与有效直径比值的五次方、泵轮转速比值的三次方以及液体密度和重力加速度的一次方成正比，即与功率量纲ML2T-3=（ML-3）L5T-3一致。

第四相似定律：它表示几何相似的液力元件，在等倾角工况下，其转矩与密度、转速和几何尺寸之间的关系。

因为N∝M·n，则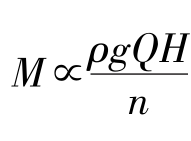，代入Q和H的量纲，可得

即几何相似的液力元件，在等倾角工况下，其转矩比值与有效直径比值的五次方、泵轮转速比值的平方以及液体密度和重力加速度的一次方成正比，即与转矩量纲ML2T-2=（ML-3）L5T-2一致。