计算机构自由度的注意事项

在利用上述公式计算机构的自由度时，还需要注意以下三方面的问题。

1.复合铰链

两个以上构件在同一处以转动副相联接，所构成的运动副称为复合铰链。在图1－9所示喷水织机的zero-max送经机构中，构件BC、CD、CF同在C处组成转动副。3个构件在C处组成了C1、C2两个转动副。同理，若有k个构件在同一处组成复合铰链，则其构成的转动副数目应为(k－1)个。在计算机构的自由度时，应注意是否存在复合铰链，以免把运动副的数目搞错。

例2　计算图1－9所示zero-max送经机构中连杆机构的自由度。

解：该机构中各构件均在同一平面中运动，属于平面机构，故可用式(1－1)计算其自由度。由图可知，机构中共有6个活动构件，A、B、D、E、F、G处各有1个转动副，C处为3个构件组成的复合铰链，包含2个转动副，无移动副和平面高副。即n=6，pL=8，pH=0，故由式(1－1)可得：

F=3n－2pL－pH=3×6－2×8=2

2.局部自由度

若机构中某些构件所具有的自由度仅与其自身的局部运动有关，并不影响整个机构的运动，则称这种自由度为局部自由度。例如，在图1－16(a)所示的平面凸轮机构中，为了减少高副元素的磨损，在凸轮1和从动件2之间安装了一个滚子3。由图可以看出，当原动件凸轮1逆时针转动时，即可通过滚子3带动从动件2作上、下往复的确定运动，故该机构是一个单自由度的平面高副机构。但用式(1－1)计算其自由度时：

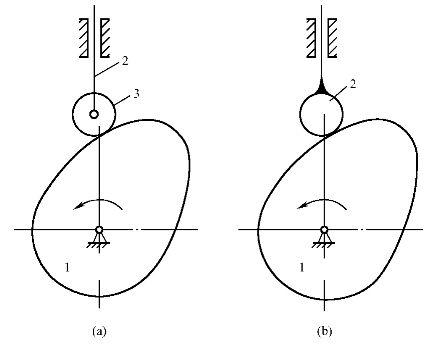
图1－16　平面凸轮机构

F=3n－2pL－pH=3×3－2×3－1=2

却得出了与事实不符的结论。这是因为，安装了滚子3和其几何中心的转动副后，引入了一个自由度(F=3×1－2×1=1)，这个自由度是滚子3绕其自身轴线转动的局部自由度，它并不影响从动件2的运动规律，故在计算机构的自由度时，应将该局部自由度除去不计。如设机构的局部自由度数目为F'，则该机构的实际自由度数为：

F=3n－2pL－pH－F'=3×3－2×3－1－1=1

得出与事实相符的结果。

既然滚子3绕其自身轴线的转动并不影响从动件2的运动，因此，在计算机构的自由度时，为了防止出现差错，也可设想将滚子3与安装滚子的构件2固结成一体，视为一个构件，如图1－16(b)所示，预先排除局部自由度，然后按自由度计算公式计算。即：

F=3n－2pL－pH=3×2－2×2－1=1

局部自由度常见于变滑动摩擦为滚动摩擦时添加的滚子、轴承中的滚珠等场合。

3.虚约束

机构的运动不仅与构件数、运动副类型和数目有关，而且与转动副间的距离、移动副的导路方向、高副元素的曲率中心等几何条件有关。在一些特定的几何条件或结构条件下，某些运动副所引入的约束可能与其他运动副所起的限制作用是一致的。这种不起独立限制作用的重复约束称为虚约束。在计算机构的自由度时，应将虚约束除去不计。

虚约束常发生在以下场合：

(1)两构件间构成多个运动副：两构件组成若干个转动副，但其轴线互相重合［如图1－17(a)中A，A'所示］；两构件组成若干个移动副，但其导路互相平行或重合［如图1－17(b)中B、B'所示］；两构件组成若干个平面高副，但各接触点之间的距离为常数［如图1－17(c)、图1－17(d)中的C、C'和D、D'所示］。在这些情况下，各只有一个运动副起约束作用，其余运动副所提供的约束均为虚约束。(www.xing528.com)

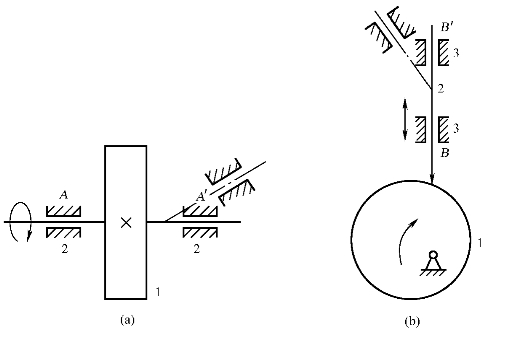
图1－17

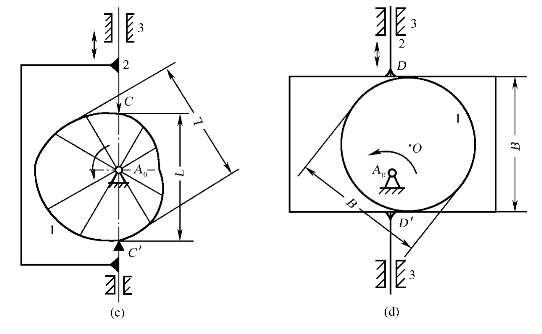
图1－17　两构件间构成多个运动副

(2)两构件上某两点间的距离在运动过程中始终保持不变。在图1－18所示的平面连杆机构中，由于A0A∥B0B，且A0A=B0B，A0A'∥B0B'，且A0A'=B0B'，故在机构的运动过程中，构件1上的A'点与构件3上的B'点之间的距离将始终保持不变。此时，若将A'、B'两点以构件5联接起来，则附加的构件5和其两端的转动副A'、B'将提供F=3×1－2×2=－1的自由度，即引入了一个约束，而此约束对机构的运动并不起实际的约束作用，故为虚约束。

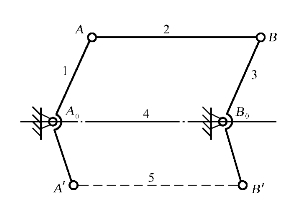
图1－18　平面连杆机构

(3)联接构件与被联接构件上联接点的轨迹重合：在图1－19所示的椭圆仪机构中，由于BD=BC=AB，∠DAC=90°，故可以证明其连杆2上除B、C、D三点外，其余各点在机构运动过程中均描绘出椭圆轨迹，而D点的运动轨迹是沿y轴的直线。此时，若在D点处安装一个导路与y轴重合的滑块4，使其与连杆2组成转动副，与机架5组成移动副，则将提供F=3×1－2×2=－1的自由度，即引入了一个约束。由于滑块4上的D点与加装滑块前连杆2上D点的轨迹重合，故引入的这一约束对机构的运动并不起实际的约束作用，故为虚约束。

(4)机构中对运动不起作用的对称部分：在图1－20所示的行星轮系中，若仅从运动传递的角度看，只需要一个行星轮2就足够了。这时n=3，pL=3，pH=2，机构的自由度F=3×3－2×3－1×2=1。但为了使机构受力均衡和传递较大功率，增加了与行星轮2对称布置的行星轮2'。增加的行星轮2'和一个转动副及两个平面高副，引入了一个约束。由于添加的行星轮2'和行星轮2完全相同，并不影响机构的运动情况，故引入的这个约束为虚约束。

综上所述，机构中的虚约束都是在一定的几何条件下出现的，如果这些几何条件不满足，则虚约束将变成有效约束，而使机构不能运动。

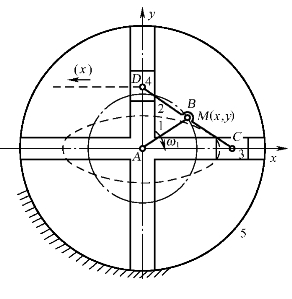
图1－19　椭圆仪机构

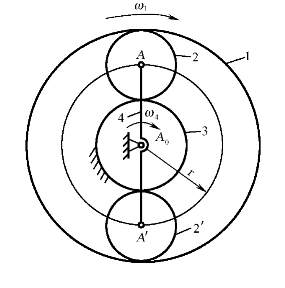
图1－20　行星轮系

需要特别指出的是，人们在设计机械时采用虚约束，都是有目的的。有的是为了改善构件的受力情况，如图1－17(a)、图1－17(b)所示；有的是为了传递较大功率，如图1－20所示；有的是为了某种特殊需要，如图1－17(c)、图1－17(d)、图1－18和图1－19所示。在设计机械时，若由于某种需要而必须使用虚约束时，则必须严格保证设计、加工、装配的精度，以满足虚约束所需的特定几何条件。

例3　计算图1－21(a)所示的大筛机构的自由度。

解：构件2、构件3、构件5在B处组成复合铰链；滚子9绕自身轴线的转动为局部自由度，可将其与活塞4视为一体；活塞4与缸体8(机架)在E、E'两处形成导路平行的移动副，将E'处的移动副作为虚约束除去不计；弹簧10对运动不起限制作用，可略去。经以上处理后，得出机构的运动简图，如图1－21(b)所示，其中N=7，pL=9，pH=1，因是平面机构，故可由式(1－1)得：

F=3n－2pL－pH=3×7－2×9－1=2

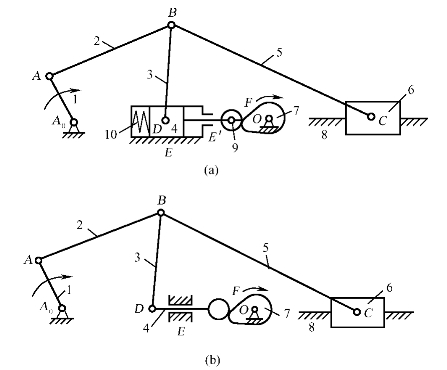
图1－21　大筛机构

由于原动件数目与自由度数目相等，故从动件具有确定运动。