数制是计数进位制的简称.在数字领域常用的数制有十进制、二进制、八进制、十六进制等.对于任何一个数,可以用不同的数制表示.
1.十进制
在计数制中,通常采用十进制,它用0、1、2、3、4、5、6、7、8、9十个数码来表示,并组成一个十进制数.十进制是“逢十进一”,即9+1=10,可以写作10=1×101+0×100,其中0是100位的系数,1是101位的系数,就是说十进制是以10为底的计数制.每个数码处于不同位数时,它代表的数值不同.例如,3467可写为
(3467)10=3×103+4×102+6×101+7×100
2.二进制
在数字电路中,为了与电路的两个状态0与1相对应,常采用二进制,它只有0和1两个数码.二进制是“逢二进一”,即1+1=10,其中0是20位的系数,1是21位的系数,因此可以写作10=1×21+0×20,即二进制是以2为底的计数制.例如:
(110110)2=1×25+1×24+0×23+1×22+1×21+0×20=(54)10
这样就将一个二进制数转换为一个十进制数.
可见,同一个数可以用二进制数和十进制数两种不同形式来表示.二进制数码与十进制数码的对照表如表7-1所示.
表7-1 二进制数码与十进制数码对照表

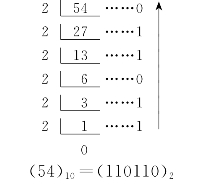
由上可见,一个二进制数可以转换为一个十进制数,而一个十进制数又如何转换为二进制数呢?它可以采用一种“除2取余(整数部分),乘2取整(小数部分)”的方法求得.即将一个十进制数整数部分不断地除2,直至商为0,取出每次的余数,先得到的余数为整数部分的低位,小数部分不断乘以2,取出每次整数,先得到的整数为小数部分的高位,于是将得到的一串二进制数组合起来,就得到一个十进制数转换的二进制数.例如,十进制数54可用如下方法求得它的二进制数.
3.八进制和十六进制
用二进制表示数时,数码串很长,书写和显示都不方便,在计算机上常用八进制和十六进制表示数.八进制有0~7八个数码,进位规则是“逢八进一”,计数基数是8.例如:
(253.8)8=2×82+5×81+3×80+8×8-1=(172)10
十六进制有0~9、A(10)、B(11)、C(12)、D(13)、E(14)、F(15)十六个数码,进位规则是“逢十六进一”,计数基础是16.例如:
(1AD.2)16=1×162+10×161+13×160+2×16-1=(429.125)10(https://www.xing528.com)
4.十进制数转换为二进制、八进制、十六进制数
对整数部分和小数部分分别进行转换.整数部分的转换可概括为“除2、8、16取余,后余先排”;小数部分的转换可概括为“乘2、8、16取整,整数顺排”.
例7-1 将十进制数[35.625]10分别转换为二进制、八进制、十六进制数.
解 (1)将十进制数转换成二进制数.
整数部分的转换:
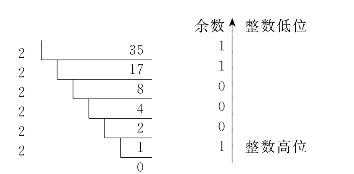
所以[35]10=[100011]2.
小数部分的转换:

所以[0.625]10=[0.101]2.
将整数部分与小数部分合起来,有[35.625]10=[100011.101]2.
(2)将十进制数转换成八进制数.

所以[35.625]10=[43.5]8.
(3)将十进制数转换成十六进制数.
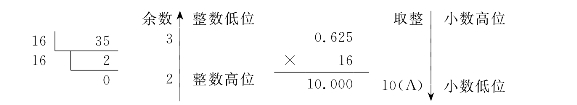
所以[35.625]10=[23.A]16.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




