RLC并联电路的谐振优化：如何实现最佳效果？

如图2-33（a）所示的RLC并联电路，在一定条件下也可能发生谐振.由于发生在并联电路中，故称为并联谐振.

1.并联谐振的条件

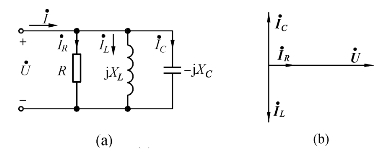
图2-33　RLC并联谐振电路及相量图

要想使电路发生谐振，应使电路的端电压和总电流同相，即

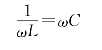
可得

式（2-42）为RLC并联谐振电路的谐振角频率和谐振频率，和RLC串联谐振电路的公式相同.

实际应用中是电感线圈和电容器组成的并联谐振电路，如收音机和电视机的调谐回路.图2-34所示即为RLC并联谐振电路，其中R为电感线圈自身的电阻.

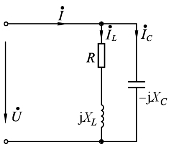
图2-34　RL与C并联电路

2.并联谐振电路的特性

当线圈电阻R很小，电路谐振时，谐振角频率及谐振频率为

一般情况下，实际电感线圈的电阻很小，在工作频率范围内，总能满足R≪XL的条件，因此，电阻的作用可以忽略不计.这样，其谐振角频率可近似等于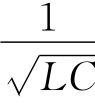，其谐振电路的特性和RLC并联电路也大致相近.

并联谐振电路具有如下特征：

①谐振时，电路阻抗为纯电阻性，电路端电压与电流同相.

②谐振时，电路阻抗为最大值.

③谐振阻抗模值为

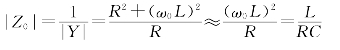
其值一般为几十至几百千欧.

谐振时，电感支路电流与电容支路电流近似相等并为电路总电流的Q倍.

电路在谐振时的端电压为U0，电流为I0，则

因此，电感支路和电容支路的电流分别为

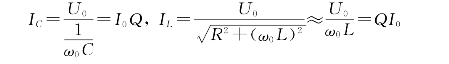
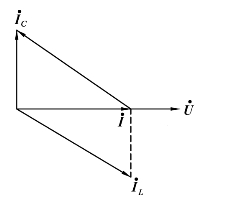
图2-35　电流相量图(www.xing528.com)

由于Q≫1，则IC0=IL0≫I0，因此并联谐振又称为电流谐振，其相量图如图2-35所示.

例2-22　由R=20Ω、L=16 mH的电感线圈和C=100 pF的电容器组成并联谐振电路.求谐振角频率、电路的品质因数.若电源采用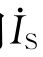=10∠0°mA的电流源供电，求通过电容的电流.

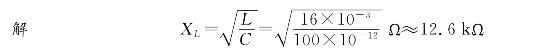
电路满足R≪XL的条件，故谐振角频率为

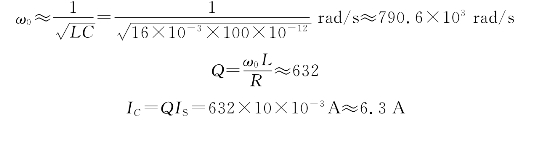
1.正弦量的概念及表示方法

正弦交流电是大小和方向按正弦规律变化的交流电，在任一时刻的瞬时值i或u是由幅值、角频率和初相位这三个特征量即正弦量的三要素确定的.可以用瞬时值三角函数式、正弦波形图、相量式及相量图四种方式来表示正弦交流电.四种表达方式各有所长，应按具体情况而定，但最常用的是相量表示法.

由于正弦交流电频率一定，只要确定幅值和初相位，其瞬时值也就确定了.因此用具有幅值和初相位的相量（复数）即可表示正弦量的瞬时值.在电工技术中常用有效值表示正弦量的大小.正弦量有效值的相量形式表示为

正弦电学量用相量表示后，就可以根据复数的运算关系来进行运算，即将正弦量的和差运算换成复数的和差运算.

相量还可以用相量图表示.相量图能形象、直观地表示各电学量的大小和相位的关系，并可以应用相量图的几何关系求解电路.只有同频率的正弦量才能画在同一个相量图中.

相量与正弦量之间是一一对应的关系，它们之间是一种表示关系，而不是相等关系.

2.数值和相位

单一参数的交流电路，是交流电路分析的基础.要重点掌握电阻、电感和电容的交流电路的电压和电流关系.

在分析RLC串联电路时，利用KVL的相量形式可导出相量形式的欧姆定律，即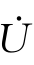=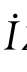Z.阻抗Z是推导出的参数，它可表示为

其中R为电路的电阻，X=XL-XC为电路的电抗，复阻抗的模｜Z｜称为电路的总阻抗.其辐角φ称为阻抗角，也是电路总电压与电流之间的相位差.｜Z｜、φ与电路参数的关系为

它们之间的数值关系可用阻抗三角形来表示.

当φ＞0时，电路呈电感性；当φ＜0时，电路呈电容性；当φ=0时，电路呈电阻性，此时电路发生串联谐振.

正弦交流电路吸收的有功功率用P来表示，P=UI cosφ，cosφ称为功率因数.

反映电路与电源之间能量交换规模的物理量用无功功率Q来表示，Q=UI sinφ.电感元件的Q为正数，电容元件的Q为负数.

视在功率S=UI=.P、Q与S可用功率三角形来表示.

功率因数cosφ的大小取决于负载本身的性质.提高电路的功率因数对充分发挥电源设备的潜力、减少线路的损耗有重要意义.在感性负载两端并联适当的电容元件可以提高电路的功率因数，并联电容后，负载的端电压和负载吸收的有功功率不变，而电路上电流的无功分量减少了，总电流也减少了.

在含有电感和电容元件的电路中，总电压相量和总电流相量同相时，电路就发生谐振.按发生谐振的电路不同，可分为串联谐振和并联谐振.

无论是串联谐振还是并联谐振，电源提供的能量全部是有功功率，并全被电阻所消耗.无功能量互换仅在电感与电容元件之间进行.