交流电路功率计算分析

在分析单一参数电路元件的交流电路时已经确定电阻是耗能元件，而电感和电容是储能元件，只在电感、电容与电源之间进行能量的交换.现分析RLC电路的能量消耗及能量交换的情况.

正弦交流电路中的功率主要包括瞬时功率、有功功率、无功功率和视在功率.仍以RLC串联电路为例，若选择关联参考方向，并设电路中的电流和端电压分别为

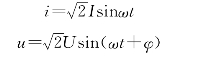
式中φ为电压超前电流的相位.

1.瞬时功率

在关联参考方向下，电路的瞬时功率为

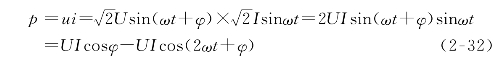
分析上式可见，瞬时功率也是时间的函数，时而为正，时而为负.表示电路时而从电源吸收功率，时而向电源返还功率，如图2-27所示.

2.有功功率

电路在电流变化的一个周期内，瞬时功率的平均值称为平均功率，即

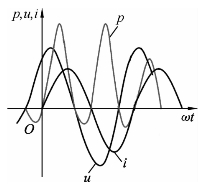
图2-27　交流电路的功率

对RLC串联电路，式（2-33）还可以表示为P=UI cosφ=URI；在RLC并联电路中电阻R是耗能元件，则有P=UIR=.显而易见，电路的平均功率也就是电阻元件所消耗的功率，反映了电路实际消耗的功率，因此平均功率也称有功功率.对于电感元件和电容元件，由于cosφ=0，因此P=0，表明两元件并未消耗功率.有功功率的单位有瓦（W）、千瓦（k W）等.

由式（2-33）还可以看出，正弦交流电路的有功功率不仅取决于电压和电流的大小，还与它们的相位差有关.为此把cosφ定义为功率因数，φ角则称为功率因数角.

3.无功功率

由以上分析可知，电感和电容虽然不消耗能量，但它们与电源之间仍存在着能量交换.为了衡量这种能量交换的规模，引入无功功率的概念.正弦交流电路的无功功率定义为

无功功率的单位为无功伏安，简称乏，符号为var.

对于感性负载电路，由于φ＞0，则Q＞0；对于容性负载电路，φ＜0，则Q＜0.电感与电容的作用不同，进行能量转换的方向相反.这是因为：RLC串联电路中通过的是同一电流，而UL与UC反相，因此，QL和QC的作用也相反.即当电感吸收电源能量，磁场增强时，电容释放能量，电场减弱；反之，当电感释放能量，磁场减弱时，电容吸收能量，电场增强.但习惯上常说电感元件“消耗”无功功率，电容元件“产生”无功功率.这样在具有RLC电路中，总的无功功率等于二者之差，即

(www.xing528.com)

4.视在功率

由以上分析可知，正弦交流电路中的有功功率和无功功率一般都不等于电压有效值和电流有效值的乘积.实际上，二者的乘积在形式上也符合功率的定义，但却不是电路中实际消耗的功率，为此把它定义为视在功率，用S表示，即

为了和有功功率、无功功率相区别，视在功率用伏安作单位，符号为V·A.

视在功率通常用来表示设备的容量，一般变压器的额定容量就是以视在功率表示的.例如，某变压器的容量为500 k V·A.

由式（2-33）、式（2-34）、式（2-36）可知

这样，有功功率P、无功功率Q和视在功率S三者也可构成一个直角三角形，称之为功率三角形，如图2-28所示.

由功率三角形可知，有功功率和视在功率的比值为功率因数，即

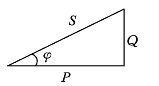
图2-28　功率三角形

在RLC串联电路中，其电压三角形、阻抗三角形及功率三角形是相似三角形.

例2-16　某RLC串联电路，已知R=10 Ω，XL=10 Ω，XC=20 Ω，电源电压=220∠0°V.试计算电路的有功功率、无功功率、视在功率和功率因数.

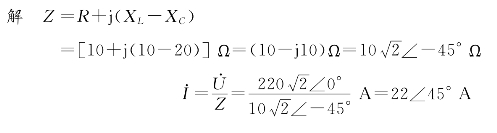
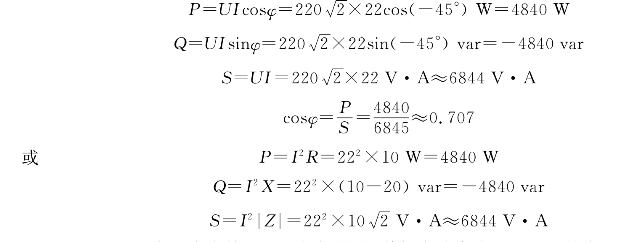
例2-17　设有一台有铁芯的工频加热炉，其额定功率为100 k W，额定电压为380 V，功率因数为0.707.

（1）设电炉在额定电压和额定功率下工作，求它的额定视在功率和无功功率；

（2）设负载的等效电路由串联元件组成，求出它的等效R和L.