RLC串并联电路设计与优化

1.RLC串联电路中电压与电流的关系

图2-18所示为RLC串联电路，图2-18（b）所示为其相量电路图，各部分电压与电流的参考方向如图所示.

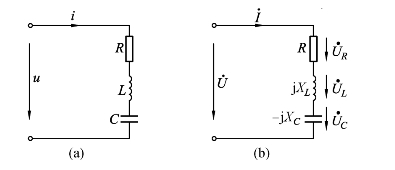
图2-18　RLC串联电路

根据基尔霍夫定律，电路的总电压为

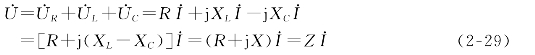
式中

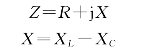
由式（2-29）可知Z是一个复数，其实部R为电路的电阻，虚部系数X为感抗和容抗之差，称为电抗，用X表示，其值可正可负.此外，Z也具有阻碍电流的作用，因此称之为复阻抗，复阻抗和电抗的单位都是欧姆.

必须注意的是，复阻抗只是一个复数，而不是正弦函数，因而也不是相量.

式（2-29）表示了复阻抗的电压和电流的相量关系，与电阻电路中欧姆定律的形式相同，称之为相量形式的欧姆定律.复阻抗Z综合反映了电阻、电感和电容三个元件对电流的阻力，也可看做一个二端元件，其图形符号如图2-19所示.

理想电阻、电感和电容元件都可看成是复阻抗的特例，它们对应的复阻抗分别为Z=R、Z=jωL、Z=-j .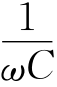

复阻抗也可以用复数的极坐标形式表示，即

式中｜Z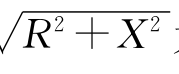｜=为复阻抗的模，称为阻抗；φ=arctan 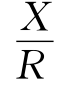为复阻抗的辐角，称为阻抗角.阻抗角的大小取决于R、L、C三个元件的参数以及电源的频率.

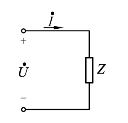
图2-19　复阻抗电路

由｜Z｜=可见，RLC串联电路中的电阻、电抗和阻抗可构成一个直角三角形，称为阻抗三角形，如图2-20所示.阻抗三角形在正弦交流电路的分析和计算中有重要的辅助作用.

2.RLC串联电路的三种情况

图2-20　阻抗三角形

在RLC串联电路中，由于X=XL-XC，φ=arctan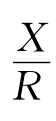 ，因此端口电压与电流的相位关系，也即电路负载的性质，有以下三种不同的情况：

（1）电感性负载.

当X＞0，即XL＞XC时，φ＞0.此时UL＞UC，电感作用大于电容作用，电路呈感性，称之为感性电路.若以电流I·为参考相量，依次画出各部分电压的相量，如图2-21（a）所示.

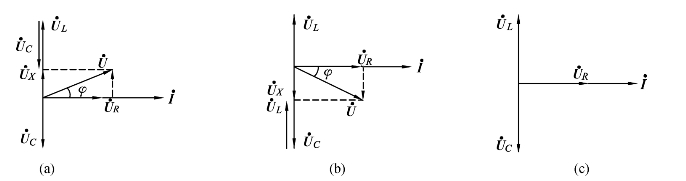
图2-21　RLC串联电路的三种情况

由图可知，U·、U·R、U·X三个电压相量构成一个直角三角形，称为电压三角形.感性电路的电压三角形位于第一象限.φ＞0，表示端电压超前总电流.

（2）电容性负载.

当X＜0，即XL＜XC时，φ＜0.此时UL＜UC，电容作用大于电感作用，电路呈容性，称之为容性电路.在容性电路中，由U·、U·R、U·X三个电压相量构成的电压三角形位于第四象限.φ＜0，表示端电压滞后总电流.相量图如图2-21（b）所示.

（3）电路谐振（电阻性负载）.(www.xing528.com)

当X=0，即XL=XC时，φ=0，表示端电压与总电流同相，电路呈电阻性.这是一种特殊情况，也称谐振，如图2-21（c）所示.

以上讨论的RLC串联电路是一种具有代表性的电路.纯电阻电路、纯电容电路、纯电感电路、RC串联电路、RL串联电路以及LC串联电路都可以看成是它的特例.这些由不同元件组合而成的电路，均可用RLC串联电路的分析方法进行分析和计算.

例2-13　某RLC串联电路，已知R=13.7Ω，L=3 m H，C=100μF，外加电压u=220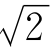sin（ωt＋60°）V，电源频率f=1000 Hz.试求电流i、电压超前电流的相位φ.

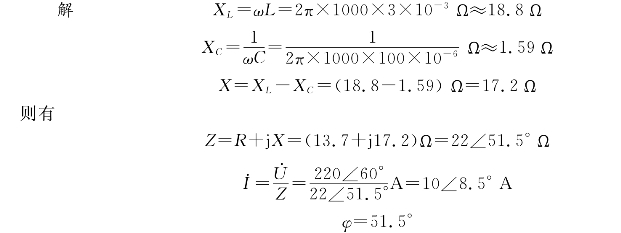
例2-14　如图2-22所示，在RLC串联电路中，已知R=150Ω，UR=150 V，URL=180 V，UC=150 V.试求电流I、电源电压U及其它们之间的相位差，并画出电压、电流相量图.

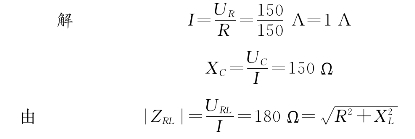
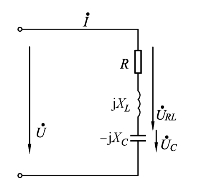
图2-22　例2-14图

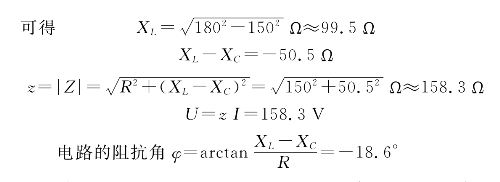
图2-23　相量图

其相量图如图2-23所示，选取电流为参考正弦量，其他电压参照元件性质及计算数值而得.

例2-15　图2-24所示为日光灯正常工作时的等效电路图.其中R为灯管电阻，L为镇流器电感.若R=300Ω，L=1.66 H，电源电压为220 V，f=50 Hz.计算电路中的电流、灯管电压和镇流器电压的有效值以及总电压和电流的相位差.

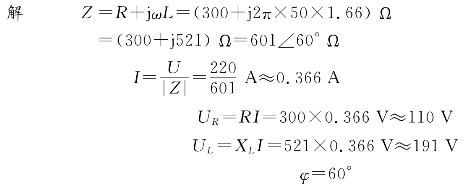
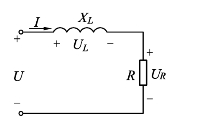
图2-24　例2-15图

3.RLC并联电路

如图2-25所示是RLC并联电路.并联电路电压相同，一般选取电压为参考正弦量，再根据各支路的负载情况，确定相应支路的电流iR、iL、iC.设电源电压为

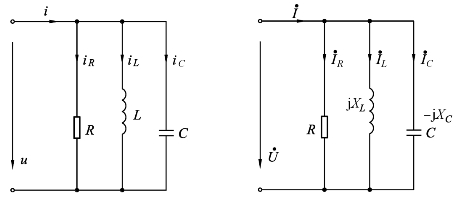
图2-25　RLC并联电路

各支路电流对应的相量为

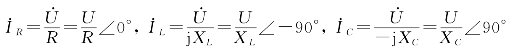
由基尔霍夫电流定律，可得出并联电路的电流相量方程：

图2-26为电压、电流的相量图.

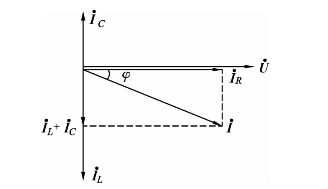
图2-26　RLC并联电路相量图