1.电感元件
电感元件是从实际的电感器（又称电感线圈，如变压器线圈、日光灯镇流器的线圈、收音机中的天线线圈等）抽象出来的理想化模型.实际电感器通常由导线绕制而成，因此总存在电阻，若忽略线圈本身的电阻，可以把线圈看做一理想电感元件.
若线圈匝数为N，而且绕制得非常紧密，可认为穿过线圈的磁通与各匝线圈像链条一样彼此交链，穿过各匝的磁通的代数和称为磁通链，用Ψ表示，单位也是韦伯（Wb）.即Ψ=Nφ.
当线圈中间和周围没有铁磁物质时，线圈的磁通链Ψ与产生磁场的电流i成正比，比例常数为此线圈的自感系数，简称自感或电感，并称为线性电感，其只与线圈的形状、匝数和几何尺寸有关，用符号L表示.当线圈中通以电流i时，在元件内部将产生磁通，此时穿过线圈的总磁通Ψ（即磁链）与电流i有如下关系：
式（2-16）中的L称为该电感元件的自感或电感.当L为一常数时，该电感为线性元件，否则为非线性电感元件.线性电感元件的电感量只取决于元件的几何形状、大小以及磁介质.
电感的单位是亨利（H），常用的单位有毫亨（m H）或微亨（μH）.图2-11所示为理想电感元件及其符号.
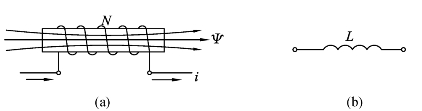
图2-11 理想电感元件及其符号
2.电压和电流的关系
根据电磁感应定律，如图2-12（a）所示，当电感中有交流电流通过时，线圈两端产生的感应电压与通过它的电流对时间的变化率成正比.其数学表达式为
式（2-17）中前者表示通过电感线圈的电流和电压的参考方向关联，后者则表示非关联.式（2-17）表明了电感元件是一个动态元件.
若设线圈中的电流参考正弦量为
根据式（2-17）可求得其端电压为
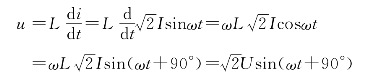
由电压和电流的表达式可得出以下结论：
①在正弦交流电路中，电感电压和电流是同频率的正弦量，且电压超前电流90°.
式中
XL与电阻相当，表征了电感线圈对电流的阻力，称之为感抗，单位为Ω.感抗和频率成正比，频率越高，电感对电流的阻力越大，因此高频交流电不容易通过电感.而在直流电路中，由于电源的频率为零，因此感抗和电感的端电压也为零，电感相当于短路.感抗和频率成正比的特性在工程技术中有着广泛应用.例如，在日光灯电路中用镇流器限制灯管电流；在收音机电路中，用高频扼流圈分离低频信号等.
③电感元件上电压和电流的相量关系为
式（2-20）叫做电感元件的相量形式的欧姆定律.式（2-20）包含两部分内容：一为电压和电流的数量关系；二为两者的相位关系.
图2-12（b）、（c）分别画出了电感电路中电流、电压的相量图和波形图.
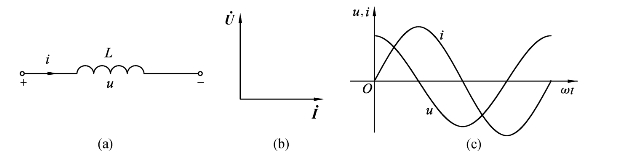
图2-12 正弦交流电路中电感电路及电压、电流波形图
例2-10 已知L=31.8 m H，端电压u=311sin（314t＋60°）V，电压和电流的参考方向相关联.(www.xing528.com)
（1）试计算感抗XL、电路中的电流，并画出相量图.
（2）如把此线圈接至220 V、1000 Hz的电源上，问通过线圈的电流等于多少？
解 （1）XL=ωL=2πf L=314×31.8×10-3Ω≈10Ω
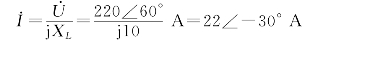
相量图见图2-13.
（2）XL=ωL=2πf L=2×3.14×1000×31.8×10-3Ω≈200Ω
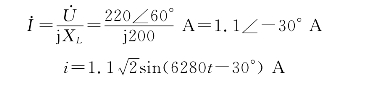
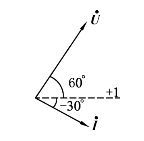
图2-13 相量图
由上面分析可知，在相同电源电压下，频率越高感抗越大，电路中电流越小.
3.电感元件的功率
设经过电感的电流的初相位为零，即为参考相量，则电感元件两端的电压初相位为90°.其表达式为
（1）瞬时功率.
由电感元件上瞬时电压与瞬时电流相乘所得.用小写p表示，即
由上式可见，瞬时功率p是幅值为UI，并以频率2ω随时间交变的正弦量，其波形图如图2-14所示.
图2-14表明：在第一和第三个四分之一周期内，u和i同为正值或同为负值，瞬时功率p为正.由于电流i是从零增加到最大值，电感元件建立磁场，将从电源吸收的电能转换为磁场能量，储存在磁场中.在第二个和第四个四分之一周期内，u和i一个为正值，另一个为负值，故瞬时功率为负值.在此期间，电流i是从最大值下降为零，电感元件中建立的磁场在消失.这期间电感中储存的磁场能量释放出来，转换为电能返送给电源.在以后的每个周期中都重复上述过程.
（2）平均功率.
指电感元件瞬时功率在一个周期内的平均值，即
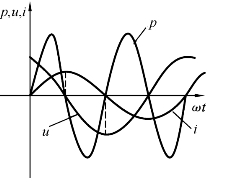
图2-14 电感电路功率
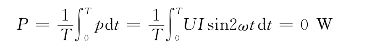
电感元件的平均功率为零，即纯电感元件不消耗能量，是储能元件.
（3）电感的无功功率.
描述的是电源与电感元件之间的能量交换，为了衡量这种能量交换的规模，取瞬时功率的最大值，即电压和电流有效值的乘积.用大写字母QL表示，即QL=UI=I2 XL=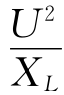
，单位为乏（var）及千乏（kvar）. （2-22）
例2-11 把一个0.5 H的电感元件接到u= 220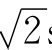
sin（314t＋45°）V的电源上，求通过该元件的电流i及电感的无功功率.
解 已知电压对应的相量为
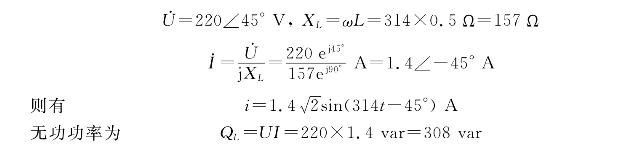
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
