1.戴维南定理内容
戴维南定理指出:任何一个线性有源二端网络,对外电路来说,总可以用一个电压源与电阻的串联模型来替代.电压源的电压等于该有源二端网络的开路电压UOC,其电阻则等于该有源二端网络中所有电压源短路、电流源开路后的等效电阻Req.
戴维南定理可用图1-38所示框图表示.图中电压源串电阻支路称戴维南等效电路,所串电阻则称为戴维南等效内阻.
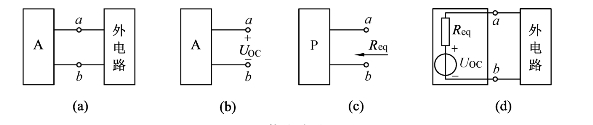
图1-38 戴维南定理分析
2.应用戴维南定理的步骤
①确定线性有源二端网络.可将待求元件从图中暂去掉,形成二端网络.
②求二端网络的开路电压.
③求二端网络变为无源二端网络的等效电阻.
④画出戴维南等效电路图.
3.戴维南定理的应用
应用一:将复杂的有源二端网络化为最简形式.
例1-17 用戴维南定理化简如图1-39(a)所示电路.
解 (1)求开路端电压UOC.
在图1-39(a)所示电路中,有
(3Ω+6Ω)I+9 V-18 V=0


图1-39 例1-17图
(2)求等效电阻Req.
将电路中的电压源短路,得无源二端网络,如图1-39(b)所示.可得
 (https://www.xing528.com)
(https://www.xing528.com)
(3)作等效电压源模型.
作图时,应注意使等效电源电压的极性与原二端网络开路端电压的极性一致,电路如图1-39(c)所示.
应用二:计算电路中某一支路的电压或电流.
当计算复杂电路中某一支路的电压或电流时,采用戴维南定理比较方便.
例1-18 用戴维南定理计算图1-40(a)所示电路中电阻RL上的电流.
解 (1)把电路分为待求支路和有源二端网络两个部分.移开待求支路,得有源二端网络,如图1-40(b)所示.

图1-40 例1-18图
(2)求有源二端网络的开路端电压UOC.因为此时I=0,由图1-40(b)可得

(3)求等效电阻Req.
将有源二端网络中的电压源短路、电流源开路,可得无源二端网络,如图1-40(c)所示,则
Req=2Ω+4Ω=6Ω
(4)画出等效电压源模型,接上待求支路,电路如图1-40(d)所示.所求电流为
![]()

电路由电源、负载、中间环节三部分组成.电路有开路、短路、有载三种状态.
电流、电压均有规定的方向,称为实际方向.在分析电路时,可选定电压、电流一个方向作为参考方向,电压、电流的参考方向是为分析电路而假设的.当选定的参考方向与实际方向一致时,计算结果数值为正,反之则为负.
基尔霍夫定律是线性及非线性电路、简单及复杂电路的基本定律,是分析电路的依据.因此,它不仅是本章的重点内容,也是分析电路的一个重点,要熟练掌握、正确运用.
电阻是耗能元件,可以串联、并联及混联.电阻串联可以分压且与阻值成正比;电阻并联可以分流且与阻值成反比;电阻混联要先整理,再用电阻串、并联方法分析.复杂电路还有星形及三角形连接且可以相互转换.
电源可以分为独立电源及受控电源.独立电源分为电压源、电流源,两种电源在一定条件下可以相互转换.
电路分析方法有支路电流法、叠加定理、戴维南定理.支路电流可应用基尔霍夫定律列方程求解,适合支路不太多的电路;叠加定理只适合于线性电路分析;戴维南定理用于求解电路中某个元件的电压或电流及功率时则较简单.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




