热传导的原理是：不同温度的物体相互接触，或物体不同温度的各部分之间，分子动能及自由电子运动传递热能，也就是温度高的物体内动能大的分子、电子把其动能传递给温度低的物体中的动能低的分子和电子，这就是热传导。热传导遵循热力学第二定律，即“热量从高温物体传向低温物体，而不可能从低温物体自动地传向高温物体”。
固体中的热传递主要靠热传导。流体中的热传递主要也是热传导，但在流体的紊流区内，流体内部的热传递往往不单纯靠热传导，还伴随着对流传热，过程较复杂。
1822年法国数学家傅里叶（Joseph Fourier）经实验总结固体热传导的过程，给出了平壁中的热传导公式。如图8-1所示为傅里叶经实验在平壁中热传导过程中热流量计算简图。在图中，假设热量Q1通过平壁单方向进行热传导而导出的平壁热传导热流量计算公式为
式中 Q——热量，单位为W；
λ——导热系数，单位为W/（m·℃）；
S——垂直于导热方向的物体的截面积，单位为m2；
ΔT——平壁两边的温度差，单位为℃；
δ——平壁厚度，单位为m。
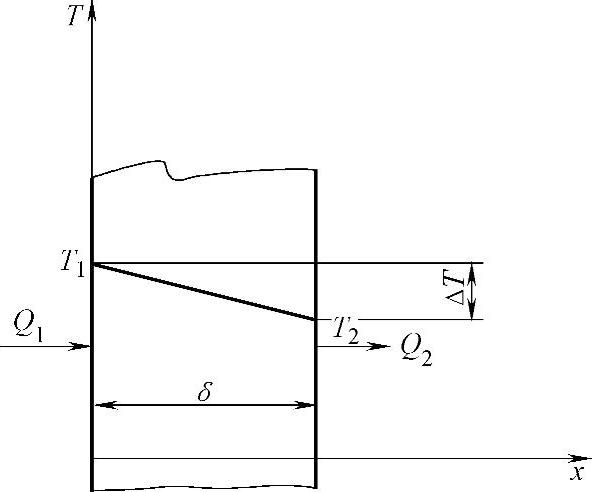
图8-1 平壁热传导
从公式中可以看到，热传导的热流量Q与物体的导热系数λ、导热面积S及物体的温度差ΔT成正比，与热传导的距离δ成反比。由于热流的方向是温度下降的方向，将式（8-1）右边加负号并写成积分形式
假定S是一个常数的热传导过程，将式（8-2）进行积分，得
Qx=-λST+C （8-3）
再假设图8-1的热传导过程是单方向的平面热传导过程，则当x=0时，T=T1，则C=λST1。将C=λST1代入式（8-3）中，得
按上面的假设，在平面单方向热传导中，温度的分布是一条直线。当x=δ时，则T=T2时，则
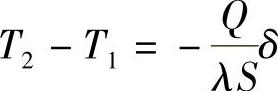
即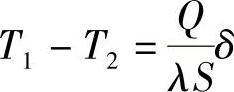
温差ΔT=T1-T2，则
将
视作热传导中的热阻Rλ，如图8-2所示，则
ΔT=QRλ （8-6）
单位导热面积的热流量称作热流密度q，即
q=Q/S=ΔT/SRλ （8-7）
q的单位为W/m2。
实际上，热分布为空间的场分布。上面的假设已将热的场分布转化为热的单方向的面分布。这与永磁发电机的实际热传递的热传导相似，从而简化了永磁发电机散热中热传导的复杂的空间热场分布计算。
热的场分布及热的传递都是空间的，它与点电荷的空间电场、永磁体的空间磁场相似。
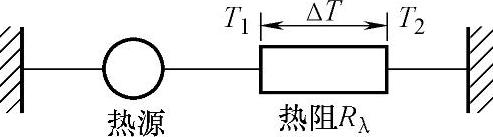
图8-2 热阻
利用热空间热场建立热传导计算公式是1842年迈尔提出来的，也就是建立了温度场与热源之间的空间的关系式，这个关系式是建立在能量守恒定律基础上的。
假定一个热源温度场产生热量Q1，它通过其体积元dv向外传导热量Q2，热源温度场剩余热量Q3，则根据能量守恒定律，得
Q1=Q2+Q3
假定介质在单位时间内，单位体积元dv产生的热量为p，则p是空间和时间的函数，在dt时间内介质所产生的热量Q1为
在dt时间内被dv导出的热量Q2为
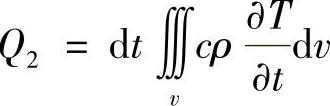
式中 c——介质比热，单位为J/kg·℃；
ρ——介质密度，单位为kg。
在同一时间内，介质内剩余的热量Q3为
式中 div（Δ2dT）——用奥氏定理计算时用的拉普拉斯算子。因热量从高温物体流向低温物体，故Q3表达式前加负号。
根据能量守恒定律
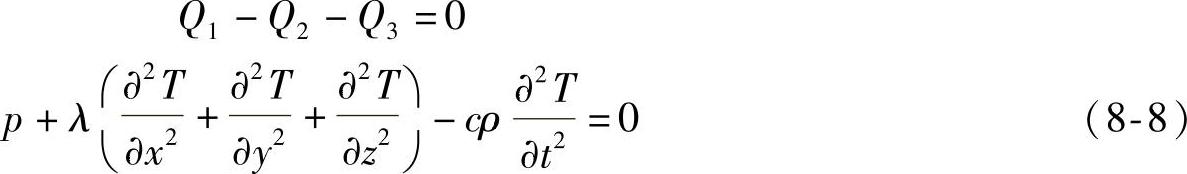
式中 Δ2dT——拉普拉斯算子，其值为
式（8-8）是介质三维空间热传导的关系表达式，它是用微分方程表示介质在三维空间和时间的关系。这是一个极其复杂的微分方程，只有给出空间边界条件及时间的起始条件等才能计算。
认为永磁发电机在强迫风冷中只沿着一个方向传热，因此，式（8-8）中的
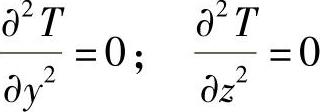
它相当于平壁热传导。
如果把定子绕组在一个槽中的导体（漆包线）视为一个热源，假设铜导体周围的绝缘材料热传导很少，可以不加考虑，因为铜是热的良导体，而绝缘材料是热的不良导体。因此，定子槽中铜导体产生的热量主要靠铜导体向绕组两端进行热传导，再由定子两端的冷却空气将热量带走，视为热传导沿一个方向，且相当于平壁热传导。
铜导体发热及沿着铜导体进行的热传导过程，可以视为热源发热及热传导是稳态的，因此式（8-8）中的
定子槽中的铜导体发热是由于铜导体内流经电流和铜导体有电阻造成的。铜导体截面积S处处相等，所以热源沿铜导体也是处处均匀分布的。但铜导体两端暴露在冷却空气中。这样，可以认为铜导体的中央温度最高。从中央向两端逐渐降低。如图8-3所示。
再认为定子槽中的铜导体发热及热量沿铜导体传导为稳态，且热传导沿着铜导体的一个方向进行，则式（8-8）成为
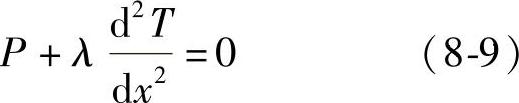
将式（8-9）中的P以铜损耗PCu代替，λ为铜的导热系数λCu，则用式（8-9）可以分别计算出定子槽中的铜导体的最高温度、平均温度、温差最大值、温差平均值。式（8-9）成为
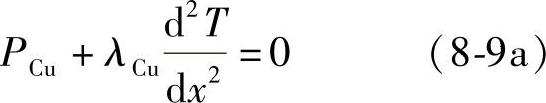
图8-3 定子槽中铜导线的温度分布(www.xing528.com)
取定子槽中铜导体的中央为原点，沿导体长Lt方向为x轴，如图8-3所示。对式（8-9a）进行积分，得
将边界条件T=T0，
代入式（8-10）中，得
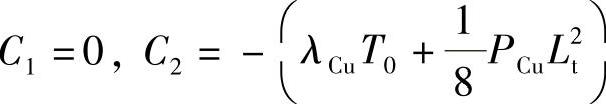
将C1，C2代入式（8-10）中，得
将x=0代入式（8-11）中，求得铜导体中央的最高温度Tmax为
式中 PCu——定子绕组铜损耗，单位为W；
Lt——定子绕组在定子槽内的长度，单位为m；
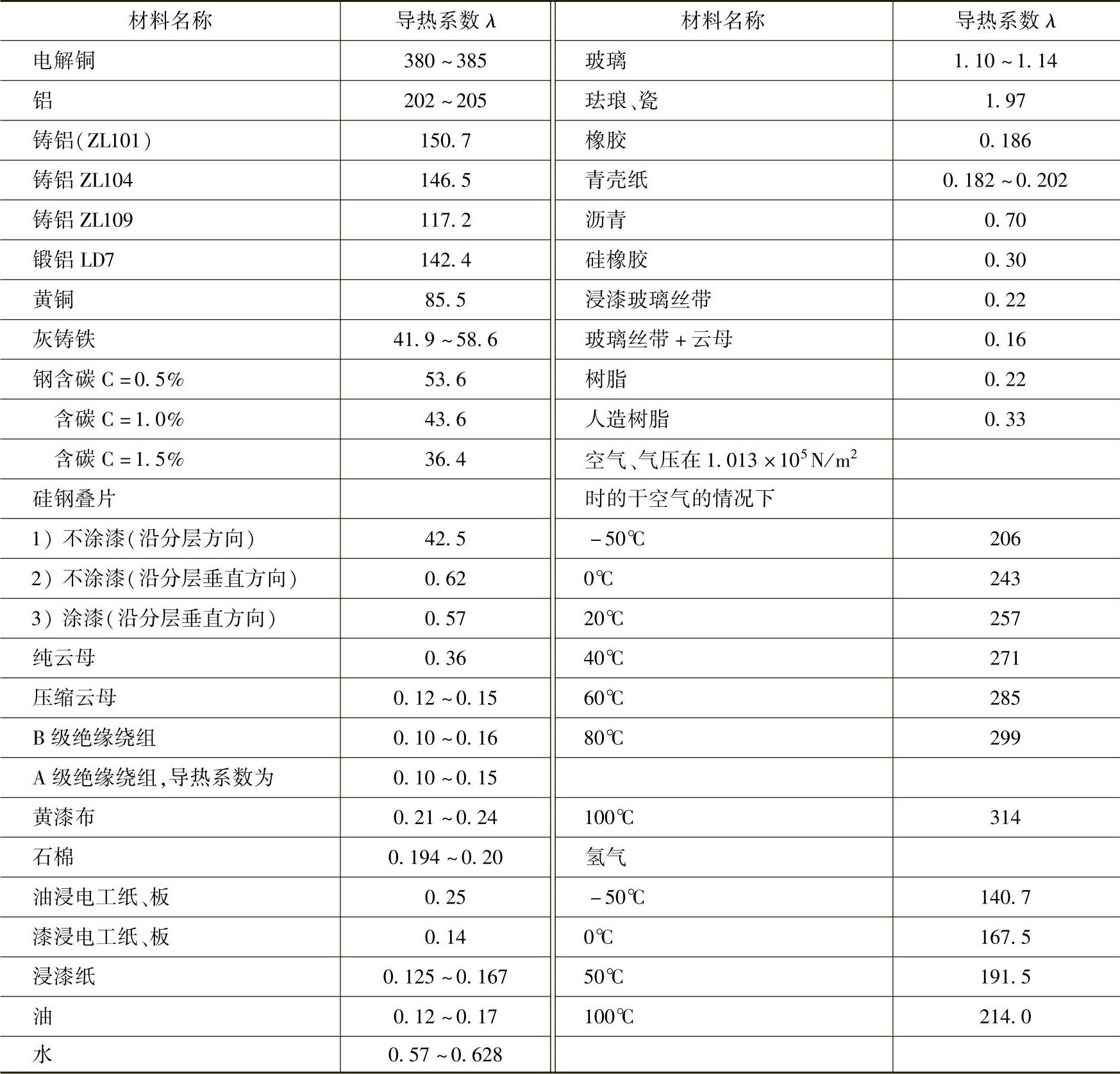
λCu——铜导体的导热系数，查表8-2。
求铜导体的平均温度Tav
求温差最大值ΔTmax
温差最大值由下式给出：
求温差平均值。
温差平均值由下式给出：
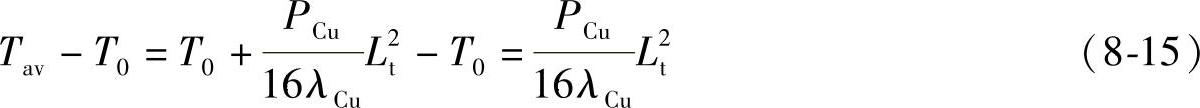
从式（8-11）可以看到，定子槽中的铜导体的温度分布是一抛物线。当铜损耗PCu产生的热量一定时，铜导体愈长，导热系数λCu愈小，则永磁发电机的温度愈高。在设计永磁发电机时应考虑定子长度Lt，Lt愈长则不仅永磁发电机温升高，冷却也困难。同时Lt愈长，则铜损耗也愈大，发电机温升愈高。但定子长度也不能太短，Lt太短会使绕组两个端部长度相对加长，铜导体的利用率降低。
同理，我们可以认为定子铁心材料是均匀的，并且铁损也是在定子铁心中均匀分布的，因而铁损产生的热也是在铁心中均匀分布的，铁心中的热分布也是向铁心两端进行热传导，并向定子两端的空气散热。这样，定子铁心由于铁损耗所形成的热也是以定子长度Lt的中心为原点的抛物线。
同理，可以得到
将式（8-16）进行积分，得
将边界条件T=T0，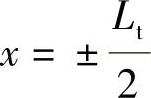
代入式（8-17），得
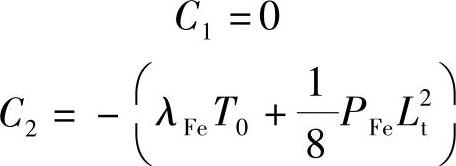
将C1，C2代入式（8-17），得
将x=0代入式（8-18）中，求得定子铁心中央的最高温度Tmax为
式中 PFe——铁心的铁损耗，单位为W；
λFe——铁心的导热系数，查表8-2；
Lt——铁心长度，单位为m；
T0——铁心两端的温度，单位为℃。
铁心的平均温度Tav为
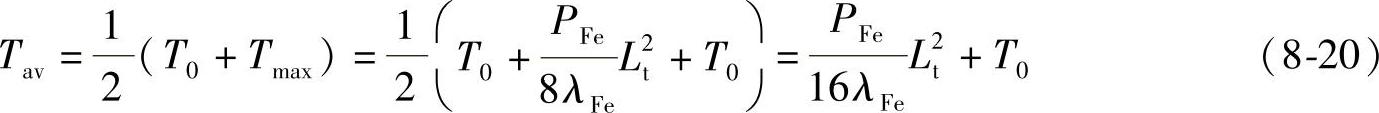
铁心温差最大值ΔTmax为
铁心的温差平均值为
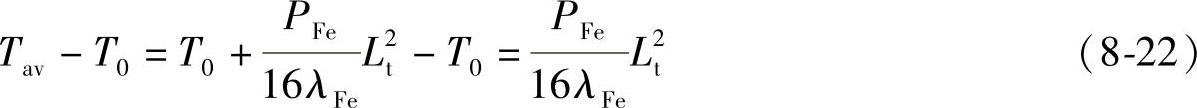
将铜损耗发热与铁损耗发热合成在一起，就是永磁发电机在运行时的各种温度。其中忽略了诸如机械损耗等损耗所引起的热量。
（1）永磁发电机运行时的最高温度Tmax
永磁发电机运行时的最高温度Tmax由下式给出：
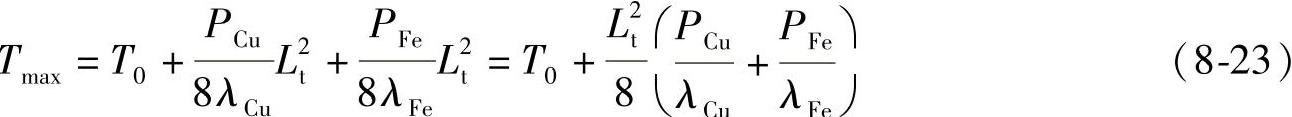
（2）永磁发电机运行时的平均温度Tav
永磁发电机运行时的平均温度Tav由下式计算：
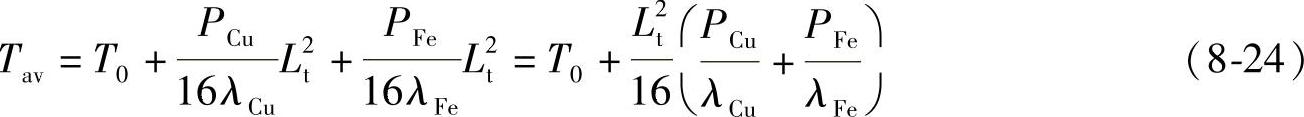
（3）永磁发电机运行时的温差最大值ΔTmax永磁发电机运行时的温差最大值由下式给出：
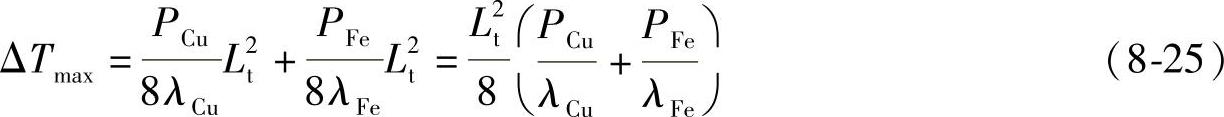
（4）永磁发电机运行时的温差平均值Tav-T0
永磁发电机运行时的温差平均值Tav-T0由下式给出：
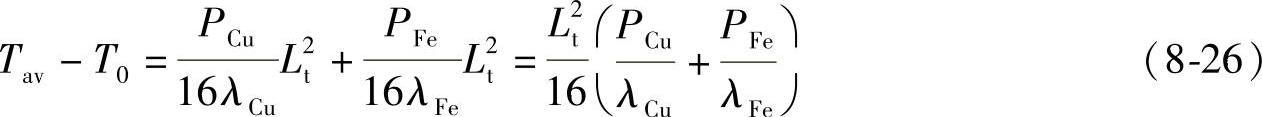
式中 Lt——定子实际长度，单位为m；
PCu——永磁发电机铜损耗，单位为W；
PFe——永磁发电机铁损耗，单位为W；
λCu——铜的导热系数，单位为W/（m·℃），查表8-2；
λFe——铁的导热系数，单位为W/（m·℃），查表8-2。
表8-2 材料的导热系数λ（W/m·℃）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
