永磁体面极式磁极径向布置的气隙磁密优化

图4-17所示为一个轴向磁化的圆柱永磁体，假设圆柱体很长，磁极面上的磁通密度均匀分布，在不考虑退磁、温度等因素的影响的情况下，极面上的磁力线密度为B_r/4π。在圆柱永磁体上方的z轴上有某点P，P点距极面的距离为OP，求P点的气隙磁密B_δ。

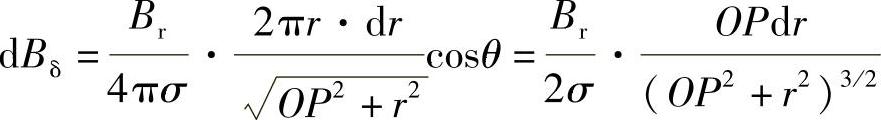
当OP=δ时，积分得

式中 B_r——圆柱永磁体的剩磁，单位为T；

B_δ——气隙长度为δ时的气隙磁密，单位为T；

δ——气隙长度，单位为m；

D——圆柱永磁体直径，单位为m。

当δ→0时，则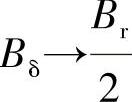。这说明了永磁体气隙磁密的最理想的最大值是其剩磁的1/2。实际上，当δ→0时，是永磁体表面的磁感应强度，在通常的情况下，B_δ也只有剩磁的32%～38%，一般绝大多数只有其剩磁的35%。

（1）两个圆柱永磁体的不同性磁极同时面对气隙的永磁体串联磁路的气隙磁密

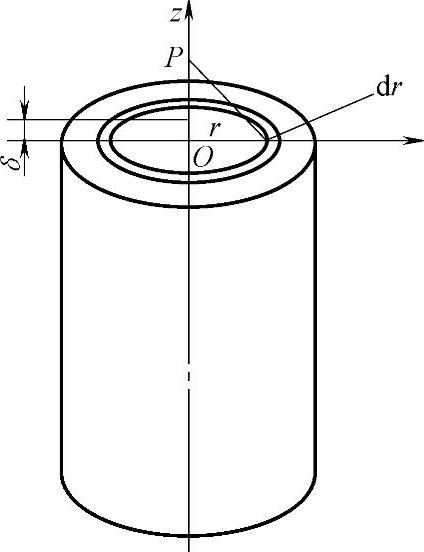
图4-17 永磁体磁面上的磁通密度计算

当两个圆柱永磁体的不同性磁极同时面对气隙所组成的永磁体磁极的串联磁路，如图4-18所示，用磁导率很高的磁导体构成磁路不长的磁回路时，则气隙磁密的理想的理论值为

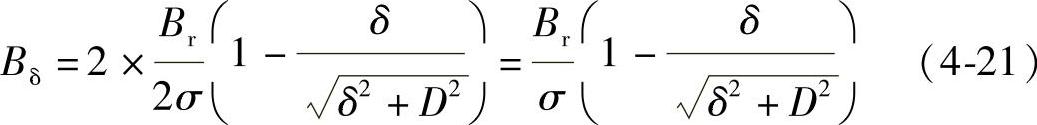
式中 D——永磁体直径，或圆柱永磁体截面相当的换算值，单位为m；

σ——漏磁系数。

等式右边之所以乘2是两个永磁体的不同性磁极同时面对气隙。

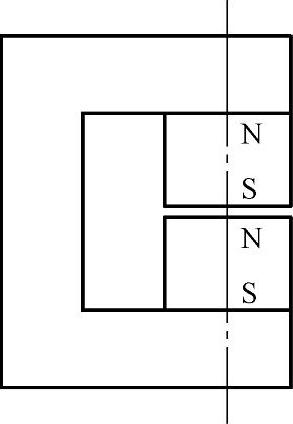
图4-18 两个永磁体不同性磁极都面对气隙时的气隙磁密

（2）矩形永磁体磁极串联时气隙磁密(www.xing528.com)

矩形永磁体的端面系数K_m：永磁体的磁感应强度不是永磁体的体积函数，而是与矩形永磁体的极面积和两极面之间的距离h_m有关。当两极面积确定后，经实测得到表4-2。经多次对不同材质、不同牌号的永磁体的磁感应强度的实测，当矩形永磁体两极面积确定后，随着两极面之间的距离增加而磁感应强度增大。当两极面距离增加到与矩形永磁体的矩形极面的短边长度相等之后，再增加两极面之间的距离，永磁体的磁感应强度增加缓慢，最后又回落到两极面距离与矩形极面短边相等时的磁感应强度值。由此可以认定，矩形极面的矩形永磁体在两极面之间的距离h_m与矩形极面短边a_m相等时，为矩形永磁体最经济的形状。

表4-2 极面为a_mb_m矩形，两极面距离为h_m的矩形永磁体端面系数

当永磁体极面为a_mb_m（a_m＜b_m）的矩形，两极面之间的距离为h_m时，其气隙磁密B_δ（T）为

式中 K_m——永磁体端面系数，见表4-4；

B_r——永磁体的剩磁，单位为T或Gs；

a_m——永磁体矩形磁面的短边长，单位为m；

b_m——永磁体矩形磁面的长边长，单位为m；

δ——气隙长度，单位为m；

σ——漏磁系数。

图4-19所示为两矩形极面永磁体的两个不同性磁极同时面对气隙并经磁导率很高的磁导体构成的永磁体串联磁回路，此时气隙磁密B_δ为

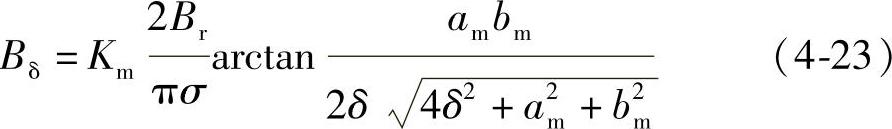
因为两个矩形永磁体的不同性磁极同时面对气隙，故在式（4-22）的右端乘以2，是2倍于单个永磁体的气隙磁密。

漏磁系数的选取：

1）径向布置的永磁体的漏磁系数σ在1.0～1.10之间选取，大功率选大值，磁路长选大值。

2）永磁体切向布置时，有非磁性材料隔磁的，漏磁系数σ=1.4～1.6；无非磁性材料隔磁的，σ=1.8～2.2。

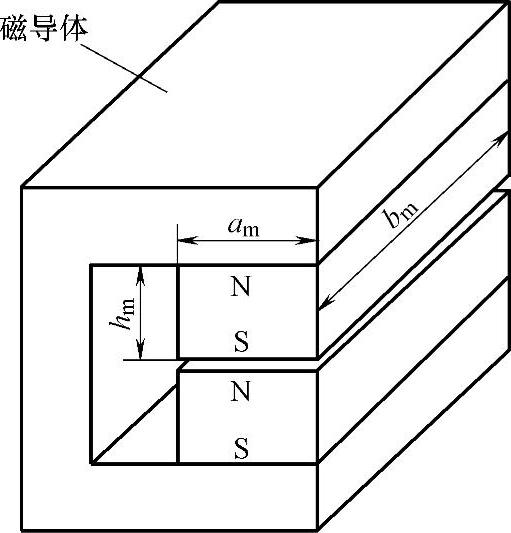
图4-19 两个矩形永磁体的两个不同性磁极都面对 气隙时的气隙磁密