测量误差合成和最小二乘法的应用

任务导入

在一个测量系统中，已知各环节的误差而求总的误差被称为合成误差。由于随机误差和系统误差的规律和特点不同，两种误差的处理方法也不同。因此引入最小二乘法对误差数据进行处理。最小二乘法在误差的处理中作为一种数据处理方法。

知识链接

1.测量误差的合成

一个测量系统或一个传感器都是由若干部分组成的。设各环节为x1，x2，…，xn，系统总的输入输出关系为y = f（x1，x2，…，xn ），而各环节又都存在测量误差。各环节的测量误差对整个测量系统或传感器测量误差的影响就是误差的合成问题。若已知各环节的误差而求总的误差，叫作误差的合成；反之，总的误差确定后，确定各环节具有多大误差才能保证总的误差值不超过规定值，这一过程叫作误差的分配。

由于随机误差和系统误差具有不同的规律和特点，两种误差的合成与分配的处理方法也不同。

1）误差的合成

系统总输出与各环节之间的函数关系为

各环节定值系统误差分别为Δx1，Δx2，…，Δxn，因为系统误差一般均很小，其误差可用微分来表示，故其合成表达式为

当计算实际误差时，以各环节的定值系统误差Δx1，Δx2，…，Δxn 代替上式中的dx1，dx2，…，dxn，即

式中，Δy 为合成后的总的定值系统误差。

2）随机误差的合成

设测量系统或传感器由n 个环节组成，各部分的均方根偏差为σx1，σx2，…，σxn，则随机误差的合成表达式为

其中，y = f（ x1，x2，…，xn ）为线性函数，即

如果a1 = a2 = … = an = 1，则

3）总合成误差

设测量系统和传感器系统误差和随机误差相互独立，则总的合成误差ε 表示为

2.最小二乘法的应用

最小二乘法在误差的数据处理中作为一种数据处理手段。通过最小二乘法获得最可信赖的测量结果，使各测量结果的残余误差平方和最小。在等精度测量和不等精度测量中，算术平均值或加权算术平均值最符合最小二乘法原理，因此可作为多次测量的结果。最小二乘法在组合测量的数据处理、实验曲线的拟合等方面均获得了广泛的应用。

例如，测量铂热电阻温度，铂热电阻的电阻值与温度之间函数关系式为

Rt = R0(1 + αt + βt2)

式中，R0、 Rt 分别为铂热电阻在温度0 ℃和t ℃时的电阻值；α、β 为电阻温度系数。

若在不同温度t 条件下测得一系列电阻值，求电阻温度系数α 和β。

由于测量中不可避免地引入误差，要想求得一组最佳解，使Rt =R0（1 +αt +βt2）具有最小误差，通常的做法是使测量次数n 大于所求未知量个数m（n >m），并采用最小二乘法原理进行计算。

方法1：线性方程组法

为方便讨论，我们用线性函数通式表示直接测量结果。假设X1，X2，…，Xm 为待求量，Y1，Y2，…，Ym 为直接测量结果，它们相应的函数关系式如下：

若x1，x2，…，xm 是待求量X1，X2，…，Xn 最可信赖的值，又称最佳估计值，则相应的估计值亦有如下函数关系：

则相应的误差方程为

式中，l1，l2，…，ln 为带有误差的实际直接测得值。(www.xing528.com)

按最小二乘法原理，要获取最可信赖的结果x1，x2，…，xm，则应使上述方程组的残余误差平方和最小，即

根据求极值条件，应使

将上述偏微分方程式整理，最后可写成

上式即为等精度的线性函数最小二乘估计的正规方程。其中

正规方程是一个m 元线性方程组，当其系数行列式不为零时，有唯一确定的解，由此可解得最佳估计值x1，x2，…，xm，即为符合最小二乘法原理的最佳解。

方法2：矩阵法

将线性函数的最小二乘法转换为矩阵计算会有许多便利之处。将误差方程（1-2-9）用矩阵表示，即

式中，系数矩阵为

估计值矩阵为

实际测量结果矩阵为

残余误差矩阵为

残余误差平方和最小这一条件的矩阵形式为

即

V′V = 最小

或

将上述线性函数的正规方程用残余误差表示，可改写成：

写成矩阵形式为

即

由式（1-2-15）有

式中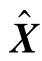，——最小二乘估计的矩阵解。

任务实施

1.解释下列名词：

（1）测量误差的合成；

（2）误差的分配。

2.讨论分析下列问题：

说明最小二乘法的原理，并指出其有哪几种计算方法。

知识拓展

最小二乘法原理在误差的数据处理中作为一种数据处理方法，试说明此法在三坐标测量中的应用。