资金的时间价值及折算公式初探

一、资金的时间价值（或称时间因素）

所谓资金的时间价值（或时间因素），是指一定量的资金在生产过程中通过劳动可以不断地增加新的价值，即资金的价值不是固定不变的，而是随着时间不断地产生增值。例如将一定量的资金用于发展生产事业，通过劳动者的劳动，除创造必要劳动价值外，还会创造一部分剩余劳动价值。前者为劳动者的工资，后者为税金和利润。单位资金所获得的利润，称为资金利润率。如果将一定量的资金存入银行，利息就是资金随时间而变的增值。为区别起见，一般将不考虑资金时间价值的经济分析方法称为静态法，考虑资金时间价值的经济分析方法称为动态法。现以银行存款为例，通过复利公式可看出动态法和静态法的差异。静态法不考虑资金的时间价值，100元在任何时候都认为还是100元。动态法则不然，如果年利率为10%。则100元在10年后应为100（1+0.1）10=259元，在50年后应为11739元；而10年后的100元在目前现值只值38.6元，50年后的100元现值只值0.85元。如果兴建一项水利工程耗资相等，一个方案工期长、开工早，另一个方案工期短、开工晚，两方案投产时间相同，效益相当。按静态法考虑，两方案投资相同，效益相等，无优劣可言。而按动态法考虑，工期长的方案消耗资金早，资金积压损失大，显然不如工期短的方案好。

因此动态法比静态法可更好地反映资金的经济效果，避免资金被无偿地积压。

二、基本折算公式

在考虑资金的时间价值时，常要进行现值P、年值A与终值F之间的折算，折算公式主要根据计算利息的复利法。所谓复利法，是指前一期的利息，作为下一期本金再计息的方法。现将基本折算公式介绍如下。

（一）现值P与终值F的折算公式

先将几个符号说明如下：

P——资金的现值，指某一时期，当时可供运用的现款；

F——终值，指现值经过n期（不专门说明时，其单位为年）到n期末的本利和；

n——期数，一般以年计；

i——利率，以百分数表示。

设某年初本金为P元，年利率为i，则第一年末利息为iP，本利和为

再将P（1+i）元作为第二年初之本金，则第二年末利息为iP（1+i），本利和为

依次类推，到n年末，终值（本利和）为

因为（1+i）n＞1，故F值总是大于P值。

上式称为一次整付复合公式，其中（1+i）n称为一次整付复合因子。

如果已知终值F求现值P，则为

上式称为一次整付现值公式，其中1/（1+i）n称为一次整付现值因子。

前述例中说明当年利率i=10%时，现在的100元10年后本利和为259元；10年后的100元现值只有38.6元，就是按式（16-1）和式（16-2）计算。

上面折算公式用于不同情况，具有不同的含义。作为研究银行存款的现值和终值的关系它是复利公式；i为利率；作为研究投入和产出的关系，i为效益系数或投资积压损失系数；作为研究不同时期货币的价值，i可作为通货膨胀系数。

（二）年值A与终值F的折算公式

先研究这样的问题：在n年中，每年年末存入相同款额A元（通常称为等额年金值，简称年值），年利率i，如何求n年年末之终值F。这种情况很简单，只要将每年的A值分别按上一节的现值与终值公式求n年末的本利和，然后总加起来，就是要求的终值F。

第一年末的年值A至n年末，中间共有（n-1）年，按式（16-1）求得n年末本利和为A（1+i）n-1；第二年末的年值A至n年末本利和为A（1+i）n-2，依次类推，最后至第n年，该年年末值A无利息，仍为A元。由此求各年至n年的本利和之总和为

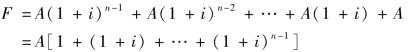
两边同乘以（1+i），得

以上两式相减，得

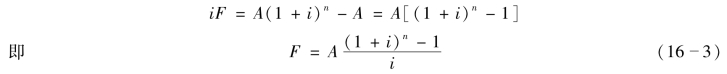
上式又可写成

式（16-3）相当于银行零存整取。其中称为等额系列复合因子。

【例1】 每年存款100元年息I=8%，如按复利计算，试问10年后本利和为若干？

式（16-4）相当于n年后希望获得一笔基金F，该款可用来偿债，或设备更新，因此每年需储存年金A。其中称为基金储存因子。

【例2】 10年后需用1万元更新一台设备，如年利率为5%，问每年年末应均匀存款多少？

（三）年值A与现值P的折算公式

在前面研究的基础上，求A与P的关系非常方便，只需将式（16-1）代入式（16-4），即得

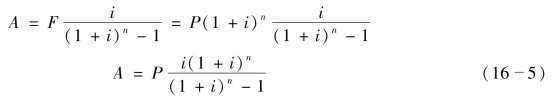
式（16-5）表示，借贷（或存入）一笔现金P，在利率为i的情况下，每年年末摊还（或取出）A元，至n年末可还清（或取完）。式中i（1+i）n/[（1+i）n-1]称为本利摊还因子，或资金回收因子。

【例3】 某水利工程一次投资10万元，年利率为5%，如希望10年内收回成本，试问每年平均受益至少为几元？

式（16-5）可改写成

式中　——等额系列现值因子。

以上从复利公式出发，介绍了水利经济计算中最常用的6个基本折算公式。为便于对照、比较和应用，现将它们汇总于表16-1。(www.xing528.com)

表16-1　基本折算公式

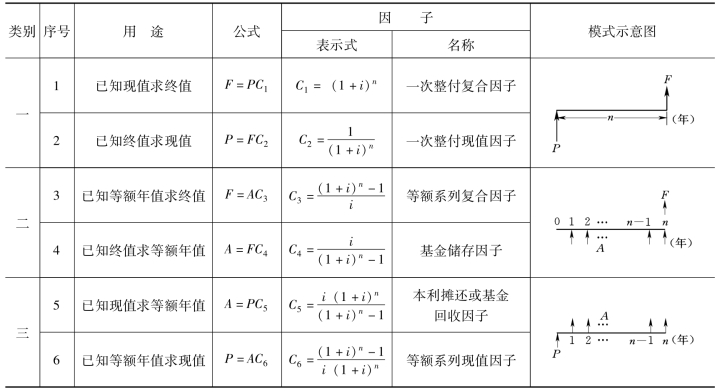
许多资料中已将上述各因子按不同i及n事先制成表供查用。

其实最基本的折算公式只有两个，即式（16-1）和式（16-3）（表16-1中为序号1和3）。只要记住这两个公式，其余折算公式均可由它们换算求得。

三、等差系列折算公式与等比系列折算公式

除上述常用基本折算公式外，等差系列（G）与等比系列（R）也是常见的两种资金流程，现将这两种系列的折算公式分别介绍如下。

（一）等差系列折算公式

1.G与F的关系式

设有一资金系列如图16-1所示。其中第一年末为0，第二年末为G，第三年末为2G，…第n年末为（n 1）G，如果年利率为i，则该系列第n年末的终值F可由下式表示

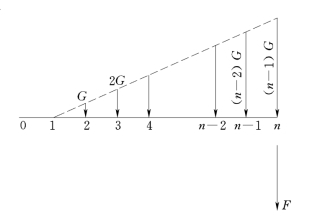
图16-1　等差系列示意图

将上式两边乘以（1+i）得

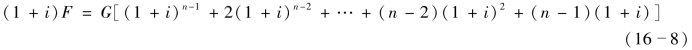
式（16-8）减去（16-7）得

式（16-9）再乘以（1+i）得

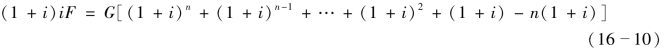
式（16-10）减（16-9）得

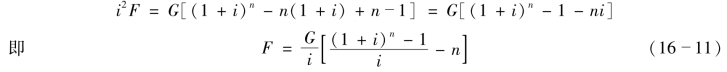
2.G与P的关系式

由（16-2）式可知，现值P与终值F关系为P=F/（1+i）n，因而将式（16-11）代入，可得

3.G与A的关系式

如果资金流程为等差递减系列，见图16-2（a）中系列a，这种情况可将它看成是均值系列b与等差递增系列c之差，见图16-2（b）。于是便可直接应用以上关系式求解。

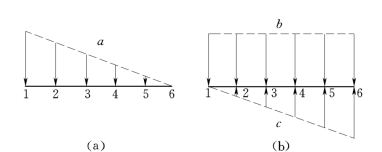
图16-2　等差递减系列计算模式

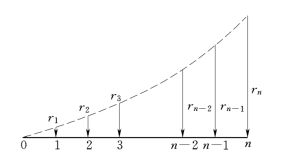
图16-3　等比系列示意图

（二）等比系列折算公式

1.R与F的关系式

设有一资金系列，每年按一定百分比（J）增长，如图16-3所示，其中r1=R，r2=r1（1+J），r3=r1（1+J）2，…，rn=r1（1+J）n-1，如年利率为i，则第n年末的终值F可用下式表示

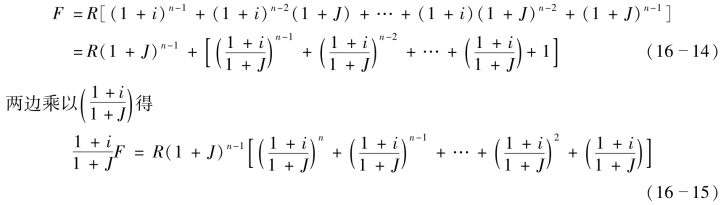
式（16-15）减去式（16-14）得

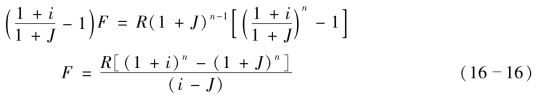
2.R与P的关系式

将式（16-16）代入式（16-2）可得

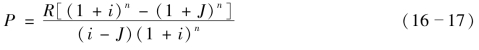
3.R与A的关系式

将式（16-16）代入式（16-4）可得

一般情况下，资金的流程可能由上述几种基本情况组成。往往需先将它分解，然后再分别进行折算。在分解时一定要留心期数n值和资金的位置为年初或年末。资金流程是具有方向性的。如取收入为正。则支出为负。

四、资金流程图与折算基准年

由上述可知，要考虑资金的时间价值，必须知道资金的数量和资金的具体收付时间。对于复杂的资金流程，为便于进行经济分析，常用资金流程图标明各项资金的位置，如图16-4所示。

水利建设项目经济评价的计算期包括：建设期（自建设项目动工兴建到开始生产前为止）；投产期（自建设项目开始生产到形成全部生产能力时为止）；生产期（自建设项目形成全部生产能力开始，到各项目规定的生产期为止）。

为了统一核算，便于综合分析与评价，常须引入计算基准年（点）的概念。它相当于图解计算中的坐标轴和原点。一般讲，基准年（点）的变动不会影响相对指标和方案比较的结果。现统一规定计算期的时间基准点为建设期的第一年初。并规定各年投资，年运行费及效益的现金都在本年末收付。

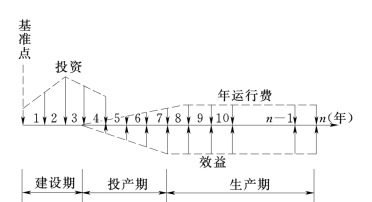
图16-4　资金流程图