水资源系统优化规划、调度及求解途径简介

一、水资源系统的特点和优化规划的内容方法

前面几节已重点介绍了用传统方法进行库群调节计算的方法。本节将说明应用近代分析技术，即系统分析方法，来研究水利系统（或库群）的优化规划和调度问题，并先从“系统”和“水利系统”的基本概念说起。

“系统”这一概念是近代科学技术高度发展的产物。它是第二次世界大战后期因军事科学和现代战争的高度综合性所促使的，并在应用于具有广泛综合性的现代科学技术和生产领域中，而形成发展的。所谓系统，一般性的定义是：“一组对象，它们具有在物理上和经济上规则地相互依赖，相互作用的关系；和在完成特定功能上相互制约，相互影响的关系。这种所构成的统一的有机整体就是系统。”

从这一涵义来衡量，水利系统正是这类系统的一个典型例证。

但是水利系统，由于水资源的固有特性，它与一般“系统”相比更为复杂，且由于对综合利用和综合管理上的新的更高的要求，因此目前典型的水资源开发管理问题，往往涉及广大的地区范围，一系列的河流流域上，多个工程、多个开发目标、多种约束、多种影响所构成的完整系统，如何合理开发和管理的问题，这也就是通常所说的水利系统优化规划、调度所要解决的课题。

水利系统的优化规划技术是近代系统分析方法在水资源领域的直接应用，其主要内容一般包括下列四个方面，即水利（水资源）系统数学模型的构作，最优化目标和准则的拟定，以及径流描述方式和模型的各种求解方法的探讨。兹分别简介如下。

1.模型问题

水利系统规划中重要的问题，首先在于建立系统模型。当把水利系统的各元素（系统变量，亦即各工程项目的主要参数），其相互关系和输入资料（包括水文径流等资料）、输出目标（如最优化目标效益，各设计变量或运行参数）等，通过一定的简化和某些假定后，用数学形式来描述表达，就成为此水利系统的数学模型。模型通常由两部分组成，一是最优化的目标函数，一般以开发效益或投资费用的形式表达。另一是约束条件组，它反映各种设备能力和资源的有限情况，或设计、运行的各种限制要求。

水利系统的数学模型，可以从不同的角度进行下列分类：

（l）确定性模型和随机模型。视模型各系数和变量是否包含随机因素。

（2）解析模型和模拟模型。当最优化目标和各约束均能以数学式表达时为解析模型。它着眼于直接求解析的或数值的最优解。模拟模型则是以数学式表达系统各环节的功能，并汇合组成模拟系统的全过程者。

（3）静态模型和动态模型。视系统变化是否与时间进程有关。

（4）线性模型和非线性模型。指目标函数和约束条件中是否包含非线性方程。

（5）规划模型和运行模型。反映系统变量是规划阶段求最优设计变量，还是运行阶段确定最优运行的运行参数。

另外，从模型的数学结构和求解技术又可分为线性或非线性规划、动态规划、混合整数规划等模型，网络、排队论、存贮论等模型，及其他运用古典数学的变分模型、动态解析模型等。

2.目标和准则

应用系统工程理论于水资源系统时，在建立反映系统主要特性和元素间相互作用关系的数学模型时，需要先明确系统最优规划或运行的目标是什么，是求什么东西最优。对于水利系统来说，有两种目标表达形式：一是以某些物理量为目标。例如电能、灌溉增产（如粮食）数量，电力系统总煤耗量，洪水淹没面积等。这些指标的局限性是优化目标中只能反映单项效益，因各不同物理量间一般不具有可比性。二是用经济量或经济指标，主要是以货币表达的一些指标，如年总净收益，年总计算费用，工程还本年限等。

对于综合利用的水资源工程而言，根据水资源系统应为广泛目标服务这一特性，目标和目标函数的确定不应只考虑单一目标，而要全面考虑综合利用各部门的需要、甚至还要考虑一些重要的，但不能以经济数字表达的，如水质，环境和社会福利的影响。这也就是多目标规划问题。它是水资源规划理论中的一个新的重要问题。

3.径流描述方法

作为水资源规划的基础和水利系统模型的输入，径流的描述形式如何，对模型的结构和成果的性质，显然有直接影响。目前常用三种形式：①确定型，包括用实测的或生成的径流系列或某些典型过程；②概率型，年或各月的径流以相互独立的频率分布曲线的形式来描述；③随机序列模型，一般考虑各时段径流间的自相关和各站间的互相关。常用的有一阶自回归模型，滑动平均模型等。他们主要用来预测或生成长系列的来水资料。

4.求解技术

首先，根据所建的数学类型，决定求解的基本方法，如运筹学各分支的各类解法。对水利系统而言，目前最常用的是线性规划和动态规划。前者有通用的单纯形解法，对大系统均可应用。近年尚发展了混合整数线性规划和0—1规划，对水利系统规划，工程选点可以应用。后一种动态规划，为一种多步决策规划。由于它不限于线性模型，并把一步多维问题化为多维一步问题，故特别适于水库调度和水利系统最优化的研究。其缺点则是模型的维数不能太高。

为了适应水利系统发展日益扩大和复杂化的情况，在求解技术方面，已更多引用系统分析和大系统的理论和方法。例如应用大系统分解原理，可把全水利系统按地域分解为各个子系统，以减少对计算机的容量要求。系统的分层和套接的方法，可以使大系统连小系统，主系统连分支系统，分段、分块求分支最优解答，进而求总的最优解。此外，对于复杂的水利系统优化规划，利用在计算机上直接模拟计算各种方案，目前已相当流行。

二、水库群优化调度

水库群的优化调度是近20年来国内外研究十分广泛的一个课题。尤其是水电站库群的发电优化调度，更是文献浩繁，方法众多，并都是通过建立优化模型来求解。

优化模型的目标函数有两类：一是以库群（多）年（平均）电能最大为目标；二是以电力系统年费用（或煤耗）最少为目标，以前者为更常用。模型可以是确定性的，也可以是随机型的。后者通常是求多年的电能期望值最大。

优化调度模型的类型，就其所用的优化方法而言，虽为数颇多，但可以归纳为三大类：一类为线性规划、非线性规划和网络等；二类为动态规划和其各种改进算法式的变种；三类为其他类型，如大系统分解模型、动态解析模型，二元组合模型等。至于模拟模型则比较少用。对第一、二类模型，共同的问题是库群数目多时，状态变量和决策变量数量甚大，即常称的“维数灾”和“网格灾”。而第二类动态规划法的各种变种，多半就是为解决“维数灾”而提出的改进算法。比较有名的有增量动态规划（IDP），渐进优化算法（POA法），降维迭代迫近法等。第三类则途径各异，并各有特色和优点。优化模型中也有考虑多目标要求，如防洪、航运之类的，则大多以约束条件形式来表达和满足之。仅少数方法应用严格的多目标规划的概念和理论。

库群调度问题根据求解所用的数学方法不同，可以有不同的数学模型。下面我们就比较常见的梯级两水电站库群的优化调度为例，介绍用动态规划法求解的例子。

由贝尔曼在1957年首创的动态规划，是在多时段中，连续（序贯）地作多步决策的规划方法。动态规划的基本目的，就是要从多时段所构成的全（调度）过程来看，能找出使某种目标（例如总效益）为最优的那一串决策。也就是说求最优决策序列。

动态规划模型通常包括效益函数逆推方程，和一系列约束条件方程。由于约束方程与其他数学规划模型相同（如流量、库位、出力等的上下限约束），故这里只说明前者。规划的目的总是求某目标值的最优化。如果每一时段（或每步）的决策代表一种效益，则目标函数就是诸时段（设共n个时段）效益累加的总和。对水电站库群的优化调度而言，此总效益就是库群的年总电能，根据第十二章所述，它是各时段水库蓄水状态及决策泄水量的函数。在动态规划中我们总是把总效益分为两部分。第一部分是面临时段（即当前一步）决策所产生的该时段的立即效益及第二部分，余留期各时段的总效益。根据贝尔曼优化原理，对于单一水电站水库的优化调度而言，可以写出以决策变量和状态变量为自变量的此总效益的函数式如下（逆算递推时）

式中　f——电能函数；

　　　V——n步过程的水库初始状态变量（库蓄水量；

　　　n——过程步数序号，n=1，2，…，N；

　　　*——最优值；

　　　h——决策变量——库水位（亦可用电站下泄流量q）；

　　　Cn——各月消落库位，即库位h的允许选择范围的约束集合；

　　　T——表示由决策h引起的一种状态的“转换”；

　　　R——面临时段的决策效益，即该时段的电能，可由第十二章式（12-8）的电能公式计算；

　　　——表示余留期的最优总电能，系由前一步的优化计算得出。

上式表示了前后两步（n，n+1），最优解间的递推关系，故常称为递推方程，或递推公式。为了应用式（15-12），逆推的动态规划运算是从最末时段n=N开始。之值根据时段初各种库位，由期末的边界条件可以直接得出，即把库水放至消落水位即为最优，所发电能最大。然后逆推考虑N-1及N两时段。在给定N-1时段初的各种库蓄水状态V的情况下，假定N-1时段的各种泄用库容h值，可求得相应的N-1时段（即面临时段）的所发电能，再根据式（15-12）加上余留期（即N时段）的相应电能，就得两时段总电能fn（V，h）。此各种fn（V，h）中之最大者，即为最优解（V，h），其相应的h即为该给定的N-1时段初库蓄状态时的两时段调节的最优决策。对其他给定的N-1时段初库位状态V，也作同上的计算，和求得最优（V，h）值。在求完N-1时段后，继续逆推求第N-2时段时，每一给定时段初库位时的最优fn（V，h），和该面临时段的最优h*值，依次类推。逆推计算直至全时期之初n=1，根据该时初已知三边界条件，即V的值，求解（15-12）式，就可得第一时段的h*。然后再顺向回代，不难得出整个最优决策序列，以上就是单一水库的优化调度求法。

对于水库群调度而言，其方法思路与上述完全相同。不过式（15-12）中面临时段和余留期电能均指水库群的总电能。如M为库群数目，则（15-12）式的右端第一项R前须加总和号，而公式中之V，h等均表示为M维的向量。

图15-8示出了以闽北库群为拦本的梯级库群有两个主水库时，用降维和逐渐迫近的动态规划法作优化调度的算例成果，包括两库的初始调度线和优化调度线（实线）。整个运算的粗框图则见图15-9。

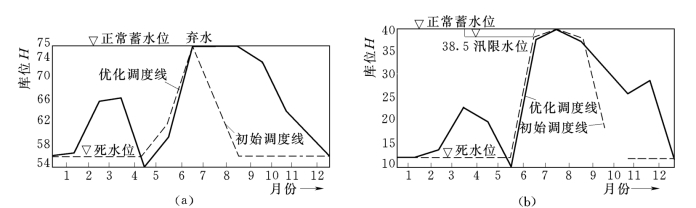
图15-8　闽北梯级库群优化调度成果

值得提到的是上述梯级优化调度的方法和程序框图，只要略作补充即可用作梯级库群补偿调节之优化计算程序，即在图15-9之第8框内插入梯级总保证出力之检验约束即可。亦即使优化调度之每月梯级总出力必须大于或等于给定之梯级总保证出力NPC，此NPC为可变动优选之变数。优选NPC是根据假定它为某一数值，然后进行长系列优化操作（使多年电能最大）之计算，再统计梯级在计算期内出力不小于NPC（即梯级保证出力不破坏）之概率是否满足总出力所需之保证率。如果不符合则增大或减少NPC值再行优化调节计算，直至符合设计保证率为止。

以上所述是对径流描述采用确定性模型者。当径流作为随机时，较常用的有随机动态规划，线性放水规则的机遇约束模型，及马尔可夫决策规划。不过，这些方法目前多半还只应用于单库或库数较少（例如2～3个）的情况。

在水资源系统的优化规划和运行问题中，应用动态规划方法已愈来愈广泛。主要原因是动态规划可使一个庞大的高维问题，化为相对较简的低维问题。它对目标函数和约束条件的函数形式限制较宽，对非线性函数和不等式约束均能方便地处理。另外对于径流描述方面，可以采用更一般的概率形式，例如前面所提到用离散的马尔可夫链来描述，从而克服了传统的时历典型的局限性。

三、整体防洪规划方案的比较和优选

（一）问题和方法

当为了某一河段城市或大片农田的防洪，削减上游来的洪水以满足安全下泄的要求时，常可采用多种措施。例如建库削洪、设蓄洪区、辟分洪道及加高堤防等。根据这些措施（以i=4，3，2，1来分别代表）的规模大小及它们间的不同组合，就构成一系列的防洪规划方案。图15-10就示出了这四类措施防洪规划的一个例子。这种防洪规划方案的优选，除了可用传统的方案比较办法外，也可用近代数学规划方法，如空间动态规划来建模和求解，简述如下。

(www.xing528.com)

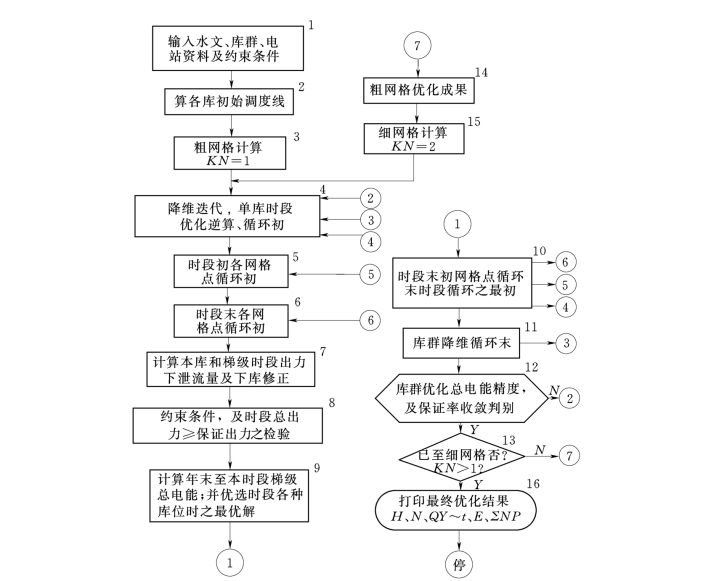
图15-9　梯级水库优化调度之计算粗框图——粗细网格逐次迫近DP法

设防洪的任务是为了将防洪点设计标准的洪水过程（见图15-11）用蓄泄分洪来削减到下游允许的安全泄量q安，也就是需要拦蓄或分泄走q安以上的成灾水量W灾（简作Wm），或者是采用加高堤防，则就需由水位——流量关系线上来求得需要增加的堤防高度，其任务也同是处理Wm这部分水量。如果用综合措施，则各项措施（i=4，3，2，1）各应分担多少，才使总的工程投资化费最少，这就是防洪整体规划的任务。

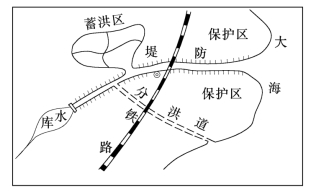
图15-10　某地区防洪措施分布情况图

前两种蓄洪措施的工程费用，决定于防洪库容、蓄洪区容积的大小，因而也与所承担的成灾水量Wi成函数关系，可以作出其折算年费用Ci—Wi的关系线。对分洪道和堤防则和成灾流量ΔQi有关，故也可作出Ci—ΔQi的关系线。然后再通过ΔQi—Wi曲线转绘成Ci—Wi线，如图15-12所示。根据四种防洪措施的特点和长处，宜把防洪库容和蓄洪区容积用于最有效的削减Wm的尖峰部分。故可由峰顶开始向下作累积曲线，如图15-11的W—Y曲线。而分洪道和堤防以承担Wm的基底部分为有利，这样使宣泄成灾水量的历时最长，泄走的洪量也最多，故由q安线向上量ΔQ转而作出相应的Ci—Wi关系线。

优化目标是在满足同等的防洪（包括可靠性）要求下，四措施单独采用或互相组合的各种方案中，总计算年费用最小的方案为最优拟选者。

为了能应用动态规划法来求解上述课题，我们把四种措施看作空间的四个阶段。决策变量di为所承担的削洪量Wi。输入输出的状态变量为设计洪水过程线的尚余的成灾水量。故可写出下列目标函数

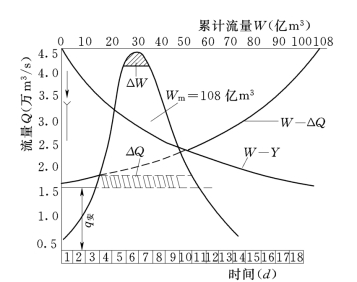
图15-11　设计洪水过程累积洪量曲线

图15-12　各防洪措施之Ci～Wi曲线

式中Wm为总成灾水量，此式用于有区间来水时（故加＞号）。各措施本身需要的约束，例如堤高加高不能超过2m；蓄洪区容积和分洪道尺寸的最大最小范围的限制，因为过小的尺寸显然是不经济的。

由于各项措施的结果是要使总的下泄成灾水量W变为零（Wm=0），或使它能安全通过下游；而上游入流为相应的设计洪水过程，故这是一个具有两端边界值的动态规划问题。这类问题宜于逆算按决策反演求解。因此决策值的假定，除各防洪措施本身的约束外，还受输出状态变量的约束。这也就是说，因水量平衡关系式（15-14），决策值也间接地受输入变量的约束。

在已知成灾部分洪水过程的情况下，在上述首尾双重约束范围内，假定一个决策di，就可求得一个年费用值Ci，它为决策di或Wi的函数，Ci改用常用符号Fi表示之如下

当决策已定为Wi时，则有

动态规划逆算的逆推公式与一般相似如下

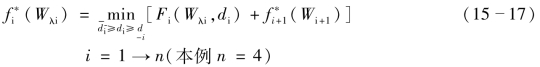
计算由第n阶段开始逐阶段逆推计算。一般情况下，四项措施i的次序编号可以任意。但当有区间水量加入，或河槽调蓄作用大时，宜按自然位置由上（游）而下地排序。今按任意自右至左：水库、分洪道、蓄洪区、堤防的次序，即水库为第4阶段就由它开始。由于为最末阶段，故其输出的成灾水量应为零。而最优决策也就是来多少成灾水量就蓄存多少，故有

然后可利用逆推式（15-17）作第n，n-1，即4，3（水库与分洪道）两阶段的局部优化计算，如一般DP法逆算的步骤进行。亦即由假定两阶段初的入流W值为0～W3，4亿立方米间各值，（注：W3，4亿为水库和分洪道之极限泄蓄洪能力之和），分别求两阶段组合最优的解。此即为式（15-17）的最右项（W入）～W入关系。下面举一个实例。

（二）一个实例的计算和成果（简介）

某地区（见图15-10）现有堤防1400km，平均堤高10m，保护着500万亩耕地和其600万居民，还有近200万人口的市镇和一铁路干线穿过。因现有堤防标准太低，只能通过16000m3/s近20年一遇，因此多次遭受较大洪水侵袭，经济损失和铁路中断影响。根据当地防洪规划，除加高堤防外，拟在上游结合发电修建一座防洪水库。并划定4个人口稀少，经济条件较差的堤垸作为分洪区。还考虑可利用有利地形，开辟一条长300km的入海分洪道，以使该地区防洪标准提高到200年一遇，相当于能防御44000m3/s的洪水。

限于地形地质条件，堤防最大高度只能加高到14m，相应可通过最大流量34000 m3/s。水库坝高只能修到68m高程，可提供的防洪库容40亿m3，（另4亿m3共用库容ΔW4）。4个蓄洪区最大蓄洪容积为22.17亿m3，分洪道最大可通过流量7200m3/s。

要求在防御200年一遇洪水的前提下，最优的上述四种措施（措施编号见前述）的组合方案，包括各措施的最优规模、参数。这是一个典型的整体防洪规划方案优选问题，故可用前面所述的空间动态规划法求解。

200年一遇的设计洪水，见图15-11。安全泄量q安16000m3/s以上的成灾水量以Wm表示，经折算总量为108亿m3。图上从峰顶向下绘出峰量累积线及由q安向上之ΔQ～W关系线，如图15-11中所示。利用此曲线，求得堤防、分洪道按均由q安向上承担泄洪流量时之极限可泄水量分别为84亿和48亿m3，我们以各措施所承担蓄、泄的成灾水量Wi为决策变量。各措施承担各种Wi水量时之费用见图15-12之各Ci～Wi曲线。（图中右半之另一条C3～W′3曲线将于稍后说明）。计算按前述以水库为第四阶段递推。由于水库的最大蓄洪容积仅40亿m3，故式（15-18）中之W4（即Wn）应从0→40亿m3取值（水库的共用库容ΔW4=4亿m3除外），并可算出其相应的费用，即式（15-18）和式（15-17）末项。然后研究水库、分洪道联合之两阶段计算，此时入流水量（扣去水库共用库容所可承担的ΔW4=4亿m3后——下同）只应从0到（40+48）=88亿m3间取值，因两措施之极限蓄泄能力相加为88亿m3。根据此0～88亿m3分为若干间隔，可由大到小作出几个W入3值。对每一W入3值，假定几个分洪道之决策d3（亦即W3），即可由递推式（15-13）求出其中最优的（即总费用最小的）两阶段决策方案。然后取另一W入3值作同样计算，直至W入3=0的方案。为了帮助具体了解，我们在表15-1中列出了两阶段的最优决策成果和相应的总费用。并在表15-2和表15-3中分别示出了当W入3-ΔW4=40和50亿m3时，表15-1中该相应成果的计算取得的过程。

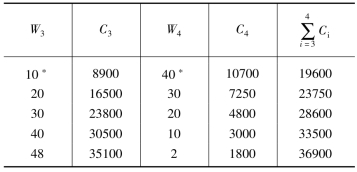
以表15-2为例，因入流W入3-ΔW4=40亿m3故表15-2中第一栏分洪道之W3只能从0→40间取值，表中分5档。每一W3值可由图15-12之C3—W3曲线中查得相应之C3，为第二栏。由40减去W3之值即得第三栏W4，并同样由图15-12查得相应之C4。最后总加C3，C4值，得第五栏总费用，并易于看出最小值为第一行之10700。于是得入流为40时，最优决策为=40，此即为表15-1中W入3-ΔW4=40这一行的优化成果。表15-3的情况完全相同，可看表自明，其中W3止于48是因此为其上限值；而W3起于10则是因为水库的上限防洪库容为40亿m3，不可能再多承担，故当入流达50亿m3时，分洪道至少要承担10亿m3的泄洪任务。表中有*号者为最优组合措施解。

表15-1　二阶段（分洪道—水库）最优解成果

注 ΔW4=4亿m3为蓄水库共用库容，为重叠用于防洪者。

可以把表15-2与式（15-17）进行对照。表中第二栏C3为式（15-17）等号右之第一项，第四栏C4为式等号右末项，表第五栏为式等号右侧方括号内值，而表中找最小之*行即为式中取min符号。最后表15-2末栏具有*之10700显然即相应于式左端最优解项

表15-2　二阶段最优解计算Wλ3-ΔW4=40

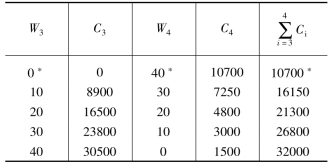
表15-3　二阶段最优解计算Wλ3-ΔW4=50

两阶段之优化计算算完后，就算二、三、四三阶段。此时入流（W入2-ΔW4）应从0→（88+22.2）亿m3间取值，同时对某一入流值，当假定了W2值后，余下（W入2-ΔW4）-W2=W3+W4之最优解，应如式（15-17）末项所示，从前面二阶段最优解之表15-1中直接查得之。三阶段算完，最后转到包括一、二、三、四之四阶段。由于第一阶段初之上边界为须处理之全部108亿成灾水量的仅一个点，故由这点可顺向回代，找出整个四阶段（即四项措施）组合的整体最优方案。计算结果得出总的年费用最小为9660万元，相应的最优防洪措施参数是：d2=0，d3=0，表示不动用蓄洪区和不开辟分洪道；W1=84亿，即堤高加高到极限14m有利；W4=20亿，表示水库设置净防洪库容20亿m3有利。详细的计算数据和表格，不细列。

应说明的是，上述最优方案的解是正确的，因为在解中两种泄洪措施——堤防和分洪道没有同时运用，只出现其中之一。如果在最后解中，属于“泄”洪类型的措施同时出现，则应重算一次进行修正。也即对单位泄量费用较高的措施本例为分洪道改用图15-12中的C3—W′3。曲线进行同上之计算。这是因为对于图15-11的成灾水量Wm言，堤防和分洪道只能有一种处于“底荷”来泄洪（类似于日负荷图中诸水电站的负荷分配），而另一种措施则只有占据前一措施之上的“腰荷”部位。也即C3—W′3中的W′3系自堤防上限流量（例如34000m3/s）之上在ΔQ—W曲线上量得者。

前面图15-12中关于堤防和分洪道的Ci—Wi曲线，系由Ci—ΔQi线和图15-12的ΔQi—W线转绘而得，而后者系从图15-11设计洪水q安以上部分取各种ΔQ时，相应的成灾水量（图中直阴影线所示）。

（三）最小费用率法

上述课题，由于主要的一些费用曲线都属凹型，故也可用更简便的“最小平均单位费用”（简称“最小费用率法”）之图解法来求解，简介如下。

根据图15-12的Ci—Wi曲线，求得曲线上各点与原点相联的各放射线的坡度，即Ci/Wi值（称为平均单位水量费用）。然后将它们点绘在以同一Ci/Wi为纵轴，W为横轴的坐标上，如图15-13所示。各措施之上下限限制条件在Ci—Wi曲线上取点时就考虑进去。例如C1/W1—W1值终于W1=84亿m3之点，它为堤防高的限值14m时所能增泄的成灾水量。在绘制了Ci/Wi～Wi的综合图15-13后，就可在此图上用水平尺由下向上移动。当水平线与各Ci/Wi—Wi线所截之Wi之和时，即得所求之最佳方案。相应最优解为F1、F2、F3、F4点之Wi值。即最优解：

此法是仿多元函数求极值的拉格朗日乘子法的原理为基础，演化、发展而导出的。利用此法对前述之防洪措施规划方案的优选算例，用同一数据之求解过程见图15-13。图中示出了优选结果为W4=20亿m3，Wl=84亿m3，W2=W3=0，可见与前面用空间动态规划法所得者完全相同。

分析图15-13，可见图中堤防洪措施i=1的C1/Wl—W1线位于最低处，说明其平均的单位水量工程费用，在各种W1水平时，均较其他各项措施为小。故W=

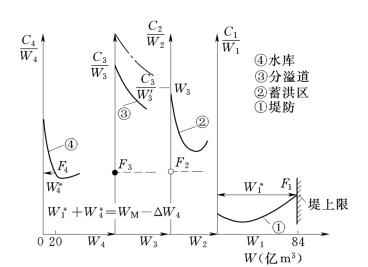
图15-13　综合图

=104亿的水平线由下向上移动时，得出首先应采用该措施，直至其极限允许值的右边界W1=84。然后水平线再向上移动，得出尚应采用防洪水库承担其余的成灾水量W1=104-84=20（亿m3）。而此水平线均未与第2、3措施之Ci/Wi线相交，说明防治所要求的设计洪水的最优整体方案，不必和不宜包括分洪和蓄洪措施，原因是该两措施的平均费用率均太高，见图15-13。

一如前面空间动态规划解法之末所提到的，为了考虑“泄”洪类措施—堤防和分洪道在图15-11洪峰过程线底部或腰部时，泄洪效果不等这一情况，在图解法时可在图15-13对单位泄量费用高的分洪措施加绘C3/W′3—W′3线以便需要时就可用。

（四）推广图解水资源优化分配问题

从上述图解方法，可见它是解“成灾水量”Wm的最优分配问题，是属于“水量优化分配”一类的问题。因此显然可将此法推广应用到“供水水资源的优化分配”等问题。特别对单水源时，更为方便。例如，如果有一灌溉水库，其调节流量q总或库总供水量W总已知，需在下游几个灌区中，按某种经济准则作最优分配。各灌区的供水量qi与相应增产效益Bi的关系曲线qi—Bi（或Wi—Bi）均已知且为凸函数。求使几个灌区总效益最大的水量分配（求各qi值）。这样的课题，就可完全仿照图15-12、图15-13的方法，由绘制Bi/Wi—Wi曲线来进行求解，或直接由Bi—Wi曲线求解。