水电站库群的补偿调节与蓄放水次序优化

一、水电站库群的补偿调节——时历法

位于流域不同地区的几个水库或水电站，由于其水文径流特征和水库调节性能，往往存在差异，当联合工作时，常可起到互相补偿的作用，大大有利于水利资源利用效益的提高。例如由于各河径流在年内分配或年际变化上的不同步性，当甲河为枯水时，乙河可能恰为丰水或平水，因此如果能够通过河道、渠系或用水部门的联系，或通过高压输电线路的连接，就可在各水库、各电站间，进行水量或电力电量的补偿调配，这就是水文补偿方面。另一方面，由于各库调节性能不同，在联合工作时，也有可能让调节性能高的（年和多年调节）水库，通过操作方式的改变，配合帮助库容不大的水库和水电站的工作。换言之，即不仅调节本河的枯水径流，也间接地调节他河枯水年和枯水季的出力，使其季节性电能转变为可靠的电能，提高系统总的保证出力，这便是库群的库容补偿方面。总之，进行各库间径流和电力的相互补偿，可以在不增加很多投资的情况下，使供水期的保证供水量或系统总保证出力显著增加，增加替代火电的容量，并使系统的供电质量亦有所改善。

水库群径流和电力补偿调节的计算方法，常用的传统方法，有时历法和混合法两种，以往还有所谓电当量法，系时历法的一种简化。近年来，用优化方法计算，亦已开始流行。本节中先介绍用时历法进行径流电力补偿调节计算如下。

如前所述，电力补偿调节的主要目的，在于提高系统总的保证出力，并使其年内甚至多年的变化过程尽量均匀，以增加其替代火电容量的效益。这种要求，在实现各电站间联网以后，由于水文自然补偿的结果，就能部分地达到。但是为了进一步发挥水库联合工作的效果。还有必要利用调节性能等条件好的一些水库（称补偿电站），来帮助条件差的水库（称被补偿电站），使后者变化无常的季节性电能，尽可能转变为可靠出力。时历法计算的特点，就在于逐个地把条件差的被补偿电站的出力过程，通过补偿电站的依次补偿，来提高和拉平总出力过程。因此首先需要对参加联合工作的水电站，进行补偿分类。

（1）划分补偿电站与被补偿电站的原则。水电站补偿能力的大小，首先决定于其所具调节电能的多少，因此库容大小，径流量多少及水头高低，是划分补偿与被补偿的主要标准。其次是各水库综合利用要求上限制条件的繁简程度。

一般说来，凡调节性能好的，库容系数β，多年平均径流Qo和电站容量、水头大的，综合利用要求比较简单的，可作为第一类补偿电站；库容、水量和水头较大者作为第二类补偿电站；而库容小的无调节和日调节水电站、及一些小电站，均可划为第三类，作为被补偿电站。

（2）统一设计枯水段的选择。由于水电站群中各水库的调节性能不同；可以有年和多年调节的，也可能仅能日调节或无调节，另外，水文条件各处也可能不尽相同，为了正确反映补偿调节后总保证出力的可靠程度；故统一设计枯水段的选择，就颇为重要，也颇为困难。一般可以按出力占系统比重较大的几个主要补偿电站所在河流的代表性枯水年组，作为全系统统一的设计枯水段。如果这样选择仍有困难（例如对跨流域补偿时），或计算成果的精度要求较高时，则以用长系列径流资料进行补偿操作为宜。

（3）补偿调节的具体计算。可先将被补偿电站，根据其已知的有效库容和设计枯水段的天然来水过程，按单库的等流量水能调节计算，推求出力过程。如有综合利用部门的要求则在操作计算中，应尽量满足综合利用要求。然后将所有被补偿电站的出力过程，同时间相加而得总出力过程，作为被补偿的对象。此后按补偿能力较小的先补，能力较强的放在最后补偿，（关于水电站群最优的调度操作方式，包括补偿次序和蓄放水次序的问题，将在下一节进一步讨论），按这样的补偿次序，分别以每一补偿电站的有效库容和天然来水，在被补偿的总出力过程线上，逐段进行补偿调节计算。由于各段来水的多少不相同，需假定各段不同的补偿后总出力来进行试算，其步骤如下：

首先按照补偿电站的径流过程，大致确定补偿水库的各蓄水段和放水段（见图15-4下T2、T1）。其次，在各段中假定一拟发的总出力N′（见图15-4上），即可求得补偿电站所需的逐月出力值，即阴影部分所示。然后根据补偿电站的有效库容及该时段的设计天然来水量，在尽量满足综合利用要求限制的条件下，进行调节至T1时段末，看水库存水是否刚刚用完放空。如果假定的拟发出力N′太大，则水库没有到T1时段末，便提前泄空了；如果N′偏小，则到时段末，水库尚存有剩余水量，这都应重新假定N′使水库能在T1末刚刚放空，此时所得的N′即为所求。这样，继续以同样的试算法进行第二时段，即T2蓄水段的补偿调节计算。此时拟发出力也应满足使补偿水库从空到正好蓄满；然后再继续下一时段的计算。

在实际运算过程中，尚应随时检验相邻两时段的拟发出力N′1、N′2间是否符合尽可能使出力拉平的原则。例如，如果补偿后某一放水段的N′1大于其后续蓄水段的N′2，说明中间水库并不需要放空。这种情况下，应该降低N′1，使水库留有部分水量，来提高后面的N′2。换句话说，前后段应归并为一段，拉平计算。同理，可推得如前后段之中间水库蓄满，则前段出力，理应大于后段出力，否则亦应归并为一段。

在假定N′时，为了避免多次试算，可以作预先的近似估算。即根据T1时段内，补偿电站的天然来水量∑Q及有效库容Vn，可按下式近似估算补偿电站可发的总补偿出力：

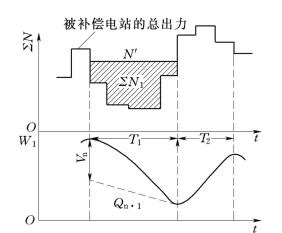
图15-4　电力补偿调节

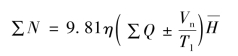
式中的正号，为放水段，蓄水段则取负号；为平均水头，系由Vt+0.5Vn查上游库位，与调节流量查下游水位之差而得。由此近似计算∑N值，在被补偿总出力过程线上，求N′线，使∑N1（见图15-4中阴影的面积）与通过上式计算之∑N相等。这样补偿调节试算，一般有一、二次，便可成功。

当第一个补偿电站的补偿调节计算完成之后，再进行第二个补偿电站计算。如此逐个地进行补偿调节计算，最后即求得系统水电站群补偿后的总出力过程和各个电站的出力过程。在此统一设计枯水段内，最低的总出力值，即为水电站群补偿后的总保证出力。如果前面是以长系列计算的，则可将每年的总保证出力，按大小依次排队，由经验累频曲线上，相应于规定的设计保证率的出力值，即为所求之总保证出力。

用时历法进行补偿调节，对综合利用要求比较容易考虑，同时能求得比较精确的补偿后出力过程。但是时历法需要试算，工作量大。当补偿电站多时，电站的补偿位置亦很难确定，因位置不同，求得过程线就不一样，以此考虑各电站的最大工作容量会相差很大。另外，对于梯级水库，当补偿位置决定后，如下游电站先补偿，上游电站后补偿，则下游电站如何考虑上游电站的调节影响的问题，也比较复杂。

二、水电站库群的联合工作和蓄放水次序

当电力系统中有几个水电站同时工作时，则参加联合工作的每一水电站都会影响其他水电站的工作情况，因为系统总的负荷是一定的。在相互影响中最重要的因素，除了各自的调节能力外，就是这些水电站间有无水力联系。因此，研究水电站库群的联合工作时，首先要区别是并联还是串联情况。下面以两并联年调节水电站为例，来说明其联合工作和蓄放水次序问题，然后再谈梯级情况。

（一）并联年调节水电站的联合工作和蓄放水次序

当有两个并联年调节水电站与火电站联合工作时，可首先把此两水电站当作一个水电站，根据它们设计枯水年的天然来水及两库的调节库容分别相加和进行水能调节计算，求出在供水期和蓄水期的两水电站总保证电能。上述调节计算也可两库分别进行，然后把各月调节电能按同时序相加。此总保证电能由于未考虑二站间的联合调度故不是最大。然后，根据两水电站的装机容量大小和上面求得的供、蓄期总保证电能，用第十二章中所述的电力系统出力电能平衡计算方法，确定二水电站在系统年（最大）负荷图上的最优工作位置。例如，一般洪水期在基荷工作，供水期则在负荷图的上部。由此得出上述两水电站的最大工作出力年平衡（过程）图[见图15-5（a）]。最后，通过各季的典型日负荷图，把此两水电站的最大工作出力年平衡图改绘为日平均出力（亦即电能）的年内过程图[见图15-5（b）]。

当此两水电站联合工作时，我们可以任意再分配在一年内所应生产的电能，所以这些水电站间分配图15-5（b）中的负荷方案是无穷多的。例如，可以一库先用水，用完后再用第二库；也可以两库同时泄用等。为了决定最佳的两水电站联合工作情况，应由下述蓄放水次序原理绘出两水电站设计枯水年各自的调度曲线。原理如下（假定两水电站的必需容量及正常蓄水位均已定）。

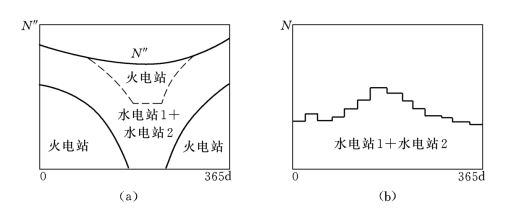
图15-5　出力的年平衡图

（a）电站最大工作出力年平衡图；（b）水电站群日平均出力过程图

年调节水电站在供水期所生产的电能可分为二部分：一为水库存水之电能，它只与水库的消落深度h消有关，与调节情况无关；另一为不蓄电能E川，它随每时刻水头即调节情况而变化颇大。因此联合工作的原则为：两水电站根据总保证电能图15-5（b）联合工作的许多方案中，能使两水电站的不蓄电能最大，或不蓄电能损失总值为最小的那个方案，可以认为是最好的。

为了求解此问题，分下列五步来说明。

（1）求不蓄出力和不足电能（出力）。对于某一昼夜来说，电力系统对两水电站所要求的总保证出力∑N，即图15-5（b）中之为已知，天然不蓄流量Q入也已知。根据两库当日的存水及水头情况，利用出力公式则总不蓄出力亦可求得：

由于是供水期，故一般∑N川＜∑N（系统要求的），需水库放水来供给的不足出力为两者之差

此∑Nv即为需二库之一，或两库共同放水来满足者。

（2）求需要消落的库水位。对某一水库来说，由水库消落可取用的流量为

如果不考虑下游水位的变化，则因

对某一天（或月）的开始时刻来说，水库的水位已知，那么落差H也已知，而相应的由水库供水Qv所得出力可由下式算得：

该式系将式（15-2）之QV代入而得者，如果式（15-1）之不足出力∑NV仅由某一库来供应则上式之NV即为∑NV。

（3）求dH间的关系。为了研究两库中哪一库放水供应有利，我们分析式（15-3）。当需要从二库中任一库单独放水满足不足出力∑NV时，各库所需要消落的库位dH值一般并不相等，而有如下的关系，因

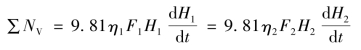
如果η1=η2，由上式右面经简化后可得

此式表示满足同一∑NV值时，两库消落值dH的大小比值。

（4）算不蓄电能损失。由于本时段消落的水位，在其后整个供水期内还将不断引起不蓄电能的损失，此损失值取决于两个因素：该时刻到供水期末的不蓄水量W川和因水库该时段供水而落差减小之值dH。

因此，如果第一库供水，则不蓄电能损失为

如果第二库供水，则不蓄电能损失为

显然，某一水库供水其不蓄能量的损失较小时，则该库先供水较有利。由前式，假定η1=η2，得第一库先供水有利之判别式为

（5）求判别式。将式（15-4）之dH代入式（15-5），并简化之，得

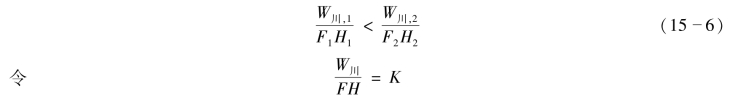
则式（15-6）变为

此为倪克勒并联水电站群联合工作最优蓄放水次序的判别式。它说明在供水期K值小的水库先供水有利。

至于蓄水期，则水库蓄水而引起水位之抬高，从而引起不蓄电能的增加。哪个水库先蓄水有利的问题，同理应根据能使蓄水所引起的不蓄电能增加最大为原则。此时可同理推得蓄水期的判别式K′为

式中　W′川——自某时刻到汛末（蓄水期末）的天然来水量减去该时刻以后水库在汛期待蓄的库容。(www.xing528.com)

判别蓄水次序与供水时相反，应以K′值大者先蓄有利。同样根据设计来水也可以绘制调度线。

（二）梯级水电站的蓄放水次序

在研究有年调节和短期调节水电站所组成梯级的联合工作时，通常以在上游设置调节程度高的水库（称为龙头水库）为有利。因为这时龙头水库在供水期内经过水库调节所提高的调节流量，同时流经下游各级水电站，因而使整个梯级的总电能增加。而此时年调节水电站的最佳消落深度也相应增加。至于水电站群的联合工作，可先作出上游年调节水电站水库的调度图，按调度图进行操作，所得的各日实际工作出力，决定其在系统负荷图上的工作位置；而下游诸短期调节水电站的工作情况，要根据各自天然流量（考虑上游梯级水库的调节影响，并考虑流到时间的长短），在本库的水头情况下，求出各日平均出力，再根据水电站属日调节或无调节来决定它在系统负荷图上的最佳工作位置（在年调节水电站工作区域的留下部分）。

梯级水电站联合工作中极重要的是，当梯级有两个具有长期调节能力的水库时，它们间的蓄放水次序。此蓄放水次序的公式，可以仿上节并联水库的同样概念和步骤来导出。所不同的是：设第一库为上库，第二库为下库，则上游水库的不蓄出力N川上应包括流过下游水库（该时水头为H下）时所发的出力。也就是式（15-3）中的H对上游库言应改为（H上+H下），而式（15-4）则应为

此外，不蓄电能损失计算中，如果下水库供水时，则由该时刻至计算期末入库之川流水量除W川下外，还应加上上水库在此期间下泄放空之水量即V上。因此公式成为

而式（15-5）相应地成为

将式（15-8）代入（15-9）即得

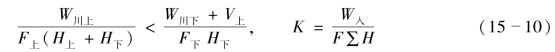
式（15-10）即为梯级水库蓄放水次序之判别式。其中W入为该库以上之总入流，包括上水库在该时刻至供水期末下泄之总水量及区间入流。∑H为该库之梯级总水头。容易推知此式为（15-6）之推广和概括。

（三）判别式的应用和问题剖析

在运行时，每一时刻或每一时段初的水库水位是知道的。如果面临时段、甚至所余供水期的各库入流，根据预报亦能知道，就可计算各水电站的K值。由K值大小即可判别该时段应由哪个水电站先供水为有利。当根据过去水文资料需作调度曲线时，同样可自供水期初满库开始由式（15-6）确定每一时刻由哪个水库供水。因此两水电站的调度曲线就可由水能计算逐时段作出。

例如为了得到根据保证图，见图15-5（b）所需的日平均出力，从供水期初正常蓄水位开始利用式（15-6）的判别不等式，总可以定出某一时刻哪个水电站应该供水。随着此水电站的供水，其库位下降，H、F随着而减小，K值逐渐增大，最后两水电站之K值将达到相等。

从此时开始，二水库应同时供水。而每一水库应以何种强度供水，或二水电站如何分配超过不蓄电能的总差额电能∑NV，则可根据计算时段末K值相等的条件借试算法来解决。

图15-6示出了四个年调节水库的水电站梯级，各库分布位置，其经济性指标Ko（=1/K）的逐月变化过程，和供水期按判别式所定出的放水次序，从图可见，7月份第一库之最大（亦即K最小）故最先放水。到a点开始1、2库同时放水，b点则表示1库已放完。其他各点见图自明。

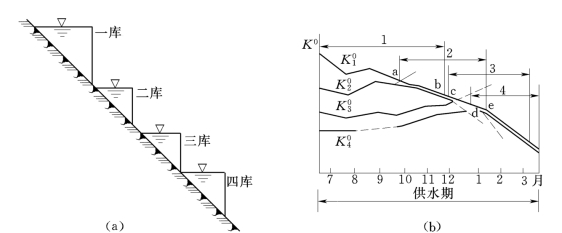
图15-6　梯级水库放水判别

（a）四水库梯级分布；（b）经济特性指标K0时历图1、2、3、4—水库消落的时期和次序

从上例可以看出，梯级工作中，一般由于上游水库来水小而梯级水头大，故其K值往往比下游水库小，只有在上游是小水库其F小时，才有可能例外。因此，按判别式进行操作时，较多情况下上游水库总是先供水后蓄水，下游水库则总是后供水先蓄水，这样才能使供水期梯级电能损失最小，而蓄水期梯级电能增加最多。这样的供水次序，原则上也适用于解决梯级中各库余水利用的先后问题。

但是，在实际计算中，由于须考虑到综合利用要求（如下游航运、灌溉、给水等）及其他限制条件（如水电站的装机容量和必需最小出力等），同时为了避免某些水库可能期末来不及泄放，发生无益弃水，往往并不绝对地按K值判别决定各水电站水库的蓄放次序，较多情况下是同时供水，仅以K值来判别决定水电站多供水或少供水的问题。例如近年来，生产部门广泛应用的混合法就是利用绘制调度图来限制不希望的情况，以与判别式相结合。此种结合的方法，还可扩大到补偿调节计算。

至于蓄水期，由于判别式K′中是没有考虑汛末可能发生弃水的因素的，为了在判别蓄放水次序的同时顾及避免弃水，各水库应根据汛期天然来水的情况，按绘各库单独的防弃水调度线的方法，从汛末开始以装机容量逆时序进行调节计算，推得水库蓄水位过程线作为具体操作的上限控制线，这样就可避免弃水。然后，在避免弃水的条件下进行判别水库的蓄水次序。另外，在特别枯水年限制出力及丰水年利用多余水量的调度规则，则各库应单独制定。

水电站群蓄放水次序的上述判别式法，根据不蓄电能损失最小的概念，简单明了。但从综合利用和技术经济等角度看，它在具体应用上，归纳起来，也还存在下列一些值得讨论和研究的问题：

（1）一般说来，此判别式宜用于两个或两个以上水库，其径流年内同期规律上具有一定的同步性者，以使各库的供蓄水期能基本一致。如果供水期不一致，发生一个水库供水，另一水库可能蓄水，则应用判别式较复杂。

（2）在一些水库群的实际调度中，当各库K值相差悬殊时，若按K值操作易使各库放水、蓄水过于集中，出力过分不均。为了在集中供水期发出很大的出力，使得各级电站都必须装有很大的装机容量，从而使得整个梯级之装机容量远远超过必须客量，使装机容量不能充分利用。此外，输电线路的费用也增加。因此，对规划而言，考虑了最优之放水次序虽使电能有一定之增加，但可能使水电站之单价及电能成本反而增加。

（3）增加无益弃水和水库蓄不满之机会。尤其在蓄水期，如下游水库尽量先蓄，不用多久就会蓄满，蓄满后就失去了调节之能力，当区间来量较大时，没有蓄满之上游水库又无法调节，而下游水库已满，因此只好弃水。而上游水库等下游各级水库都蓄满后再蓄水，则可能丰水期已近结束。没有多少水可蓄，这样一来使梯级保证出力和电能可能反而有所减小。

同样地，对供水期下游水库后放，也可能当轮到放水时，丰水期已至，来不及放空而被迫弃水。

（4）对防洪不利。由于位于最下游的水库能控制以上之全流域面积上之洪水，为了能最有效地拦蓄和控制洪水，应尽量使控制面积较大之下游水库腾空，上游水库先蓄。因此对防洪而言，最好是在汛期自上而下逐级蓄水比较有利。

（5）对发电以外之其他综合利用用水部门而言，在供水时与发电要求相反，先泄用下库存水，以便梯级有更大的调节灵活性，可以拦蓄流域中任一部分流来之多余来水量，常能达到最大的保证供水量。

基于上述原因，对综合利用的水库群，为了达到最大综合效益，应该通过全面考虑，协调矛盾，来拟定最终的蓄放水方式，或者用下述的混合法或优化法来进行蓄放水。

（四）混合法和优化法简介

1.混合法

蓄放水次序判别式法在单独应用时，既然有上述一系列不足之处，故近年来我国生产部门发展了把判别系数K和调度图相结合的方法，可称之为混合法。此法任务亦在对梯级水电站进行补偿调节，使水电站群的保证出力最大，年电量又尽可能多。其他综合利用要求则以约束条件方式来满足。此法对来水，认为面临时段（一般为月）的各库入流可知。当时各库库位亦已知，故如能对面临时段进行优化调度，例如前述之K判别式法，则就可一时段一时段地调度下去。但为了避免前述的问题，故在没有长期精确预报的情况下，由按历史资料绘制的各库调度线来控制。这些调度线主要为蓄水控制线和供水控制线两条，如一般调度图所述。但另外还需绘制表示全梯级总蓄能调度变化的调度图。此图的纵坐标已不是库位，而是梯级每时刻的总蓄能（如图15-7所示）。此总蓄能乃是每时刻梯级各库的蓄能值之和。而后者，当已知各库库位时，由相应的蓄水量和水头，即可算出。

上述水电站群总调度图绘制的目的，是为了保证整个水电站群的正常运行达到设计保证率的要求。并在遇到较丰的来水年份时，加大出力，以减少弃水，多发电能。遇到保证率以外的年份，水电站群的正常运行遭到破坏时，使破坏深度能满足设计要求。此总调度图有三条基本调度线：最大蓄能线，上调度线和下调度线，如图15-7所示。

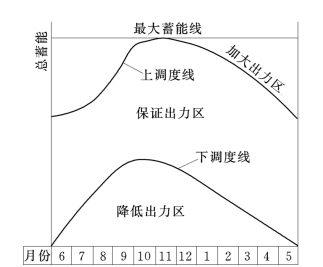
图15-7　总调度图

最大蓄能线，是各个水库都蓄满时的调度线。此数值可通过各库满蓄时的有效蓄水量及相应的利用水头算得。

上调度线是为了枯水段开始前库群能蓄满，丰平水年又能在满蓄前及时加大出力，以减少弃水。此线一般可由接近设计保证率的连续枯水段作为各电站来水典型，由蓄水期末逆向按水电站群发设定的保证出力∑NP，扣除各库当时的川流出力后，根据K判别式所定的各库蓄供次序，并考虑各种约束和各库调度图作控制而定的泄水量多少，来算出各库时段初的库位和相应的蓄能值。然后总加之即得水电站群的总蓄能，即为图15-7上调度线上的一点。同理继续逆向计算。但这样的一个典型来水所得的保证出力不一定最大，并会随所选来水过程分配的不同而变，则由长系列操作适当修正上调度线，以使库群总保证出力能达最大。

下调度线的作用在于遇到保证率以外的枯水年份时，能及早降低出力，避免破坏时深度过大。它亦由规定标准的最枯年份来水作为典型，由供水期末库空开始，按发出允许的降低出力值，结合K判别系数来逆算绘制，然后长系列操作，以作校核和必要时的修正。

综合以上所述，其调节计算的步骤如下：

（1）假定水电站群的总保证出力及允许的降低出力。

（2）由全径流系列的统计分析选出适当的典型年，根据各单库的具体条件及假定的各库最小保证出力（由系统需要来定）和降低出力，绘制各单库的调度图，包括蓄供两期最小出力的蓄供控制线和装机容量的蓄水控制线等。由各库的调度图结合1中假定的数值和K判别式，绘制出水电站群的总调度图，如前面已说明的。

（3）对全部径流系列逐时段进行操作计算如下：

1）根据各水库时段初的有效蓄水量计算水电站群的总蓄能。

2）根据时段初总蓄能点在总调度图上的位置确定水电站群在面临时段的总出力。

3）根据时段初各水电站的天然来水流量计算出各水库均不蓄不供时水电站群总的天然出力。

4）比较总的天然出力和要求水电站群发出的总出力之间差值的大小，以确定当前水库群应该供水还是蓄水来满足对水电站群总出力的要求。当天然出力不足时，由水电站群供水补足，天然出力有余时，由水库群蓄入多余水量。

5）在各单个水库调度线的控制下，根据各库判别系数决定的水库蓄、供水次序，通过试算确定各个水库的蓄水或供水数量，同时也就确定了各个电站的出力分配，一个时段的调度就完成了。

（4）待全部时段计算完毕后，统计水电站群总出力低于保证出力的破坏时段数。若破坏时段数多于设计保证率允许的破坏时段数，则减小保证出力；反之就加大保证出力，重新按上述步骤进行调节计算，直到符合设计保证率的要求，保证出力也不能再加大了为止。

2.优化方法进行水电站群补偿调节计算

用优化技术进行跨流域或梯级水电站库群径流电力补偿调节的方法，为数已较多。但总的可分为两大类。第一类是以水电站群联合优化调度的方法为基础。优化目标为使梯级（或库群）总保证出力最大，又使梯级总电能尽可能地多。这类方法很多是以动态规划（DP）方法的各种改进算法为基础，假定一个总保证出力值（有时还可加上破坏深度约束）作为约束，然后进行使总电能最大的长系列优化调节计算。由计算结果统计所假定出力的保证程度（亦即破坏次数）。如保证率大于规定的设计值，则提高总保证出力值、再算，直至其保证率符合要求为止。所用方法，在动态规划方面，有例如：降维迭代算法（亦称逐次迫近法）、增量动态规划法、POA法（渐进优化算法），二元DP法等。其动态规划的递推方程，同第四节式（15-12），此外还可用动态解析法，网络算法等其他类型方法。

第二大类是以求总保证出力最大来建立模型，亦即Max—Min模型（“最大的最小”模型）。其概念是：在每一库群联合调度方案中求出最小月平均出力值，（此即保证出力之意）。而在不同的诸调度方案中，选上述“最小月平均出力值”为最大的那一个方案，即为最大的“最小（保证）出力。”用数学式表示如下：

式中　d——调度方案；

　　　K——库群数目；

　　　i——时段号。

这类方法中，亦有好几种算法式，如：动态规划法，二时段滑动求优法，四方和最小法等。此第二类方法，亦可在求出最大总保证出力后，再用长系列径流，或丰、平、枯代表年求满足上面所得的总保证出力要求下，求多年平均电能最大的调度方案。这就体现了在枯水段来水较枯的年份，主要保证能发所要求的总保证出力，而在丰、平水年则力求多利用水头和减少弃水，以使总电量尽量大，甚至接近最大。

具体方法可参看有关文献，这里不再作深入介绍。