如何计算水库的调洪量？

一、洪水调节计算原理

水库调洪计算的直接目的，在于求出水库逐时段的蓄水、泄水变化过程，从而获得调节该次洪水后的水库最高洪水位和最大下泄流量，以供进一步防洪计算分析之用。

图13-2　水量平衡示意图

水库调洪演算要遇到两种情况，一种为下泄流量受控制的调洪演算，其控制调节方式由水库防洪运行规则（应与执行一定泄流量的闸门开启程序相区别）决定。这只能在有闸门控制的泄洪设备条件下才存在。对于这种情况，逐时段的调洪递推计算只使用时段水量平衡方程便可求出逐时段水库泄流量及蓄水量变化过程。

另一种情况为自由泄流条件下的调洪演算，无闸门溢洪道泄流、或设闸门的泄洪设备闸门开启程度一定的条件下泄流属此种情况。对此种情况，若按静库容条件考虑，须联解水库水量平衡方程和相应水库蓄泄方程才能实现逐时段的调洪演算。对调洪过程中任一Δt（Δt=t2-t1）时段，计算式可表示如下（见图13-2）：

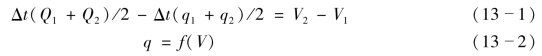
式中　Q1、q1——时段初入库、出库流量；

　　　Q2、q2——时段末入库、出库流量；

　　　V1、V2——时段初、末水库蓄水量。

蓄泄方程q=f（V）表示闸门开度不变条件下水库蓄水量与泄流量间关系；当属无闸门自由溢洪道时为水库泄流能力曲线。q=f（V）方程或曲线，可按泄洪设备类型尺寸（或闸门开度）的水力特性换算制作。若为无闸门表面溢洪道，其泄流公式为

式中　B——溢洪道净宽；

　　　h1——堰上水头；

　　　m——流量系数。

　　　ε——侧收缩系数。

若为底孔泄流，则泄流公式为

式中　ω——孔口出流面积；

　　　h2——孔口中心水头；

　　　μ——孔口出流系数。

根据式（13-3）、式（13-4）可换算求得水库水位Z与泄流量q的关系q=f1（Z），如图13-3中的Z—q曲线。进而由库容曲线可换算求得水库蓄水量V与q的关系q=f（V）。

于是，在Δt时段的调洪演算中，可由已知的Δt、Q1、Q2、q1、V1联解式（13-1）、式（13-2）求得q2和V2。依时序逐段递推计算，可求得该次洪水的水库蓄水和泄水的全过程。

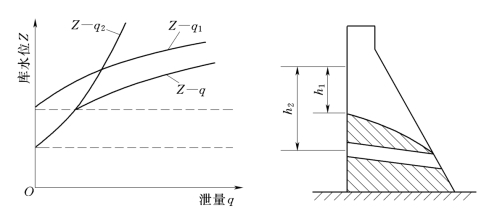
图13-3　泄洪设备水力特性及q=f1（Z）曲线示意图

二、调洪演算的基本方法

（一）列表试算法

对于控制泄流情况，采用列表法十分方便，具体计算与第二章中所述相同，不多述。对于自由泄流情况，则须联解式（13-1）和式（13-2）。然而解析求解不可能，须通过试算求解。对任意的Δt时段，其Q1、Q2、q1、V1已知，欲求q2和V2，其步骤是，假定V2（或q2）后，代入式（13-2）可求得q2（或V2），再以此q2（或V2）代入式（13-1）算得V2（或q2），若计算的与假定的一致，则试算完成，否则重新假定V2（或q2），直到满足为止。现用算例说明如下。

某水库的泄洪设备由一个开敞式无闸门溢洪道和一个泄洪底孔组成。根据它们的水力特性先计算出底孔全开情况的q=f（V）曲线（见表13-8第2、3栏），然后按表13-7所列试算。其步骤是；先将入库洪水过程依时间顺序填入第1、2栏，并计算时段（取为2h）平均入库流量填入第3栏。洪水开始进入水库时水库水位（即起调水位）为溢洪道堰顶高程774.00m，随着入库流量增大泄洪底孔闸门逐渐开启以控制下泄，使泄量等于来量，库水位维持774.00m不变，表中25日20时以前属于此种控制泄流情况。随后，因底孔闸门已全开而来水量仍在继续增大，故进入自由泄流情况，库水位被迫上升，故25日20时之后的泄量及水库蓄水量须试算求得。对25日20时至22时的时段调洪来说，可先假设时段末水库蓄水量填入第7栏，再由q=f（V）曲线得时段末泄量填入第4栏，计算第5栏和第6栏的数值后可算得一个时段末水库蓄水量去与假设值比较，看是否一致，否则重新试算，直至满足为止。再转入下一时段的计算。表13-7中所需成果系通过编制程序由计算机连续演算完成的，十分方便。水库最高洪水位和最大下泄流量出现在26日8时。

表13-7　水库调洪列表试算法

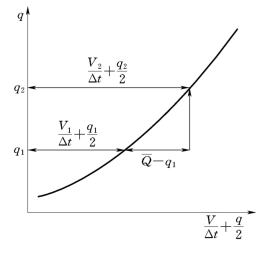
图13-4　洪水演算单辅助线法

（二）调洪演算辅助线法

联解式（13-1）和式（13-2）方程的调洪计算方法很多，在此只介绍一种较常用的单辅助线法。

先将式（13-1）改写成

式中　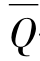——Δt时段平均入库流量。

式中左端各项均为已知值，使用式（13-2）可制作q—V/Δt+q/2关系曲线（见图13-4），以此作为辅助曲线，便可避免调洪演算中的试算，而可按图13-4箭头所示方法进行演算。其步骤是，由时段初的泄流量q1查q—V/Δt+q/2曲线得V1/Δt+q1/2值，加上值后得V2/Δt+q2/2值，再回查q—V/Δt+q/2曲线可得到q2；查q—V曲线可得到V2。随后可转入下一时段的计算。现仍以前例说明如下。

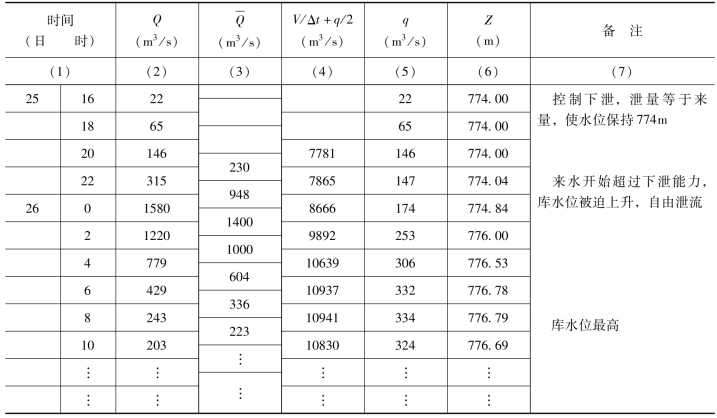
先由表13-8计算出泄洪底孔全开情况下的q—V/Δt+q/2曲线，由第3、6栏的关系表示。表中第1、2栏的关系为库容曲线，第2、3栏的关系为水库泄流能力曲线。再按表13-9的列表格式可计算出水库下泄流量过程和水库蓄水量（或蓄水位）变化过程。其计算可仍通过编制程序由计算机连续演算完成。计算结果和前面的列表试算法结果（见表13-7）基本一致。(www.xing528.com)

表13-8　水库调洪演算辅助曲线计算表

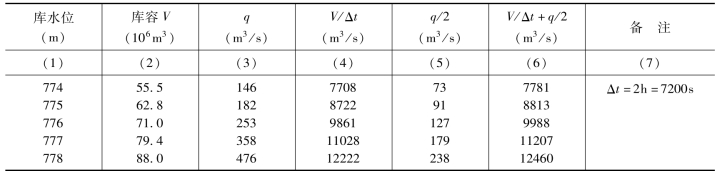
表13-9　水库调洪计算表

（三）简化计算法

在小流域、小型水库缺乏资料且水库只有无闸门溢洪道的情况下，设想将入库与出库流量过程都简化为三角形（见图13-5）时，则入库洪水总量为

对于图13-5（a）情况，水库起调水位在堰顶高程时水库最大下泄流量为

式中　Qm——洪峰流量；

　　　T——洪水历时；

　　　Vm——滞洪库容。

对于图13-5（b）情况，水库起调水位在堰顶高程以下，但充蓄到堰顶高程的时间小于涨洪历时T1，水库的最大下泄流量为

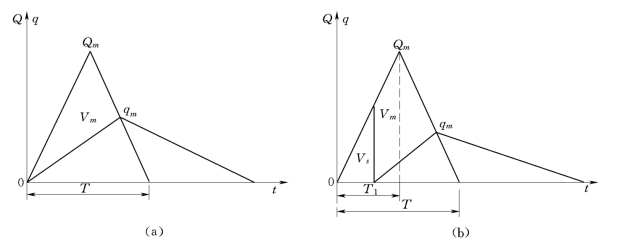
图13-5　调洪演算简化三角形法

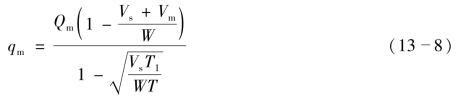
式中　Vs——蓄洪库容；

其他符号同前。

式（13-7）、式（13-8）都是从水量平衡角度建立起qm与Vm的关系式的，还必须与泄流能力曲线q=f（V）联解，才能求得qm与Vm。在具体计算时仍可由试算或图解求得。

三、考虑动库容的调洪演算

前面介绍的已广泛使用的调洪演算方法采用的都是静库容曲线，即近似地假定了调洪时水库水面为水平并平行升降。而实际上水库水面并非水平，且有时水面坡度变化还相当大。因此严格说来，调洪演算应采用水面坡度变化的动库容曲线。

根据水库区地形的一般特性，动库容主要集中在入库段而受入库流量影响较大，故水库的实际蓄水量可表示如下：

式中　Z——坝前水位；

　　　Q——入库流量。

将式（13-9）关系绘制成以Q为参数的曲线簇即为水库动库容曲线（见图10-8）。

就固定不变的洪水入库断面而言，水库蓄水量V由与坝前水位Z相应的静库容Vs和与水面坡度有关的楔形库容Vd组成。从水力学上看，在坝前水位一定的条件下，入库流量愈大则动库容愈大；在入库流量一定的条件下，坝前水位愈高，入库断面以下的天然河道槽蓄容积被淹没后变成静库容的愈多，则动库容愈小。由此特性可知，动库容的大小由坝前水位和入库流量所决定。其在调洪过程中的变化可表示为

式中　——正值；

　　　——负值。

从实际的防洪设计需要出发，动库容在一次洪水调节中所起的作用，关键在于用动库容曲线进行调洪与用静库容曲线进行调洪所得到的坝前最高洪水位（或最大下泄流量）有何差别。

对于不受闸门控制的自由泄流情况，从入流开始大于出流的时间到水库最高洪水位出现的调节时期内，尽管其间水库水面曲线经历了许多变化，但就该调节时期之始、末而言，入库流量属于增大而使动库容增加；水库水位属于升高而使动库容减小。而终究是增加或减少，则取决于其始、末入流、库位的增幅和其入库段水库地形的综合影响。由于通常都按静库容曲线作调洪演算，如果动库容在调洪始、末没有变化，则考虑与不考虑动库容作用的结果是一样的；如果动库容增加，则不考虑动库容作用计算得到的水库最高洪水位更高，这偏于安全；如果动库容减少，则不考虑动库容作用计算得到的水库最高洪水位更低，这是偏于不安全的。对于这最后一种情况，应有足够的认识和估计，这时就往往需要采用考虑动库容作用的方法进行调洪演算。

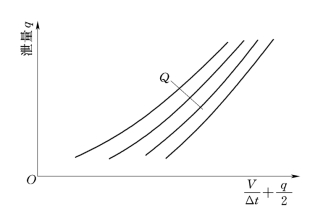
图13-6　动库容调洪演算辅助曲线

考虑动库容的调洪演算，可用类似于前述静库容调洪中建立单辅助线的方法，由动库容曲线绘制一簇以入库流量为参数的曲线（见图13-6）后进行。演算时，根据时段初、末入库流量选用相应曲线，由时段末V/Δt+q/2值可确定其下泄流量。逐时段进行计算，可求得水库下泄流量过程和坝前水位过程。

对于受闸门控制的泄流情况，由于水库水量（调节）的蓄泄平衡计算是按一定的防洪运行规则受人为控制，实际调节过程中动库容变化的影响可在实时运行过程中不断地得到校正，故不考虑动库容调洪作用的计算结果，对水库防洪安全的不利影响（如果存在的话）将比自由泄流情况小得多。

在实际问题中，由于水库地形复杂，入流断面也分布在各干支流上，因此动库容的变化也将是复杂的，故必须要有较多的精度较高的资料，才能使按动态库容曲线进行的调洪演算得到正确的结果。

鉴于动库容对调洪的影响实际上常有存在，它与有时难于推求的入库设计洪水问题联系在一起后，会使问题进一步复杂和困难。因此，对于重要的水库，尤其是平原和浅丘地区河道入库段很长的水库，应深入分析入库洪水和动库容对调洪的影响问题，以便当采用静库容调洪时，在应用计算成果上留有余地。

最后，要提到一点的是，要严格地考虑洪水波通过水库时在水库沿程的水位、流量等水力要素变化按不稳定流运动进行调洪演算，涉及到更多的水力学问题，将要求较多且严格的资料.否则，将难以保证成果精度。同时，严格的算法计算工作量亦很大。所以，当无特殊要求时，前述方法已够应用。