为了克服把总库容硬性地划分成年库容和多年库容的缺陷,以及为了在计算中可以详细地考虑水库操作方式及需水量,损失水量及水库蓄水量的变化。高尔德(Gould,1961)在莫兰水库存储理论及其模型的基础上提出了这种方法。为清楚起见,借助于具体的数值说明如下。
设有N年实测资料如表11-3所示,表中只列出了5年作为例子。总有效库容为600(m3/s).月,均匀需水流量100m3/s。试求水库供水保证率。计算步骤如下。
1.划分水库蓄水状态
把水库库容划分成k种状态,其中第0种状态为库空,而第k-1种状态为库满。在空库与满库之间,把总库容V划分成相等的k-2份,每份的库容增量为
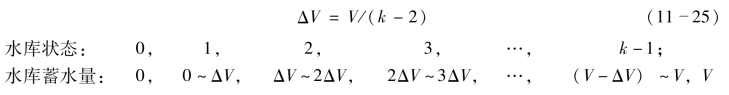
表11-3 实测流量资料 单位:m3/s
状态划分得越多,即k越大,精度越高,但要求计算机容量和计算工作量越大。泰奥(Tech,1977)建议,k的数值选择如下:

作为说明问题例子,仅取k=4,故ΔV=600/(4-2)=300[(m3/s).月],4种状态如下:

2.求水库状态转移概率矩阵
对本例而言,每年初水库蓄水量只可能有4种状态,即状态0(库空),状态1[蓄水量150(m3/s).月],状态2[蓄水量450(m3/s).月]及状态3(满库)。
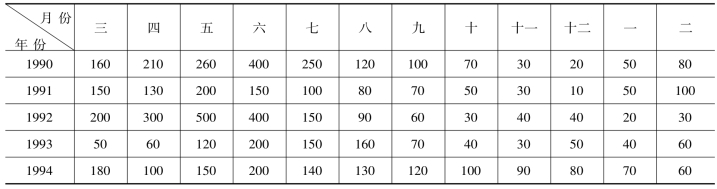
对于每种状态,分别研究实测资料中各年的水库工作情况。先研究年初水库处于状态0(库空)时的情况,用本章所讲的径流调节计算方法中的列表法、图解法等进行调节计算,可求得各年末水库蓄水量及水库正常供水破坏情况,其结果如表11-4所示。
表11-4 年初与年末水库状态
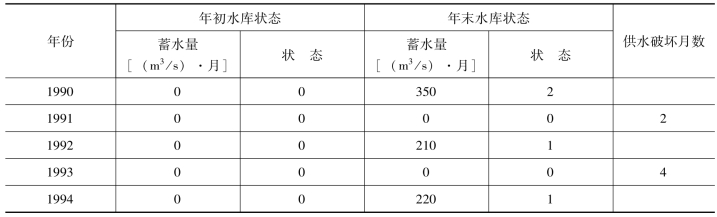
年初为库空时,若遇1990年来水过程,年末水库蓄水量将为350(m3/s).月,处于状态2,称此为状态转移,用状态转移矩阵来表示。并可在表11-5的状态转移矩阵中相应格内注上该年。例如,按此规则可将上述的结果搬到表11-5中时段初状态为0的那一列中去。显然,每列之总年数一定与实测资料的年数N相等,对本例而言为5年。把表11-5中每个元素中的年数除以N即得转移概率,它表示年初水库处于状态0的话,年末水库可能仍处于状态0(几率为0.4),也可能处于状态1(几率为0.4)或状态2(几率为0.2)。
类似地可以研究年初水库处于状态1、状态2及状态3时之状态转移情况及概率,把计算结果填入表11-5的相应列中。
表11-5 状态转移概率
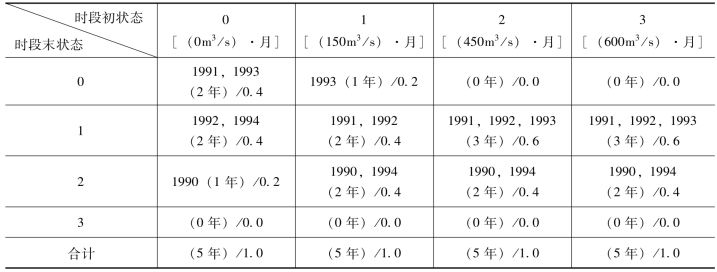
表11-5所示的状态转移矩阵,取决于来水特性、需水要求、水量损失及水库操作方式等,但对每年来说,此矩阵是固定不变的。
3.求供水破坏几率与水库初始状态的关系
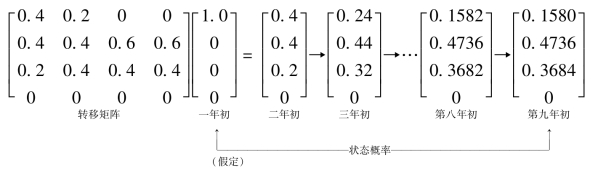
在用径流调节方法计算水库状态转移的同时,可以求得正常供水破坏的情况(见表11-4)。例如当年初水库状态为0时,五年中破坏二年,即破坏几率为0.4(破坏几率按年计),或五年中破坏6个月,即破坏几率为6/(5×12)=0.1(破坏几率按月计),供水破坏几率只与水库年初状态有关。(https://www.xing528.com)
同理,对时段初水库状态为1、2、3用同样方法计算破坏几率,计算结果如表11-6所示。
4.计算水库稳定状态概率
作为计算的起点,可以先任意假定第一年初水库的状态,例如从状态0开始,进行概率演算,即由状态转移概率矩阵与年初库位状态概率作矩阵乘积可计算第一年末水库之状态之概率。第一年末水库状态概率即为第二年初之状态概率,用同样的方法计算第二年末水库状态概率。以次类推,可求得第三、四年、…之水库状态概率,计算到第九年末水库状态概率。其计算结果如下:
表11-6 破坏几率与年初水库状态的关系
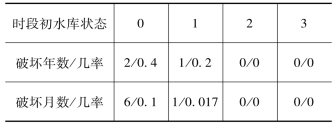
求解稳定状态的方法除了上述逐年计算外,还有其它两种方法,一种是转移概率矩阵逐次平方法,和解联立方程组法。后者要点是:因为对于稳定状态有
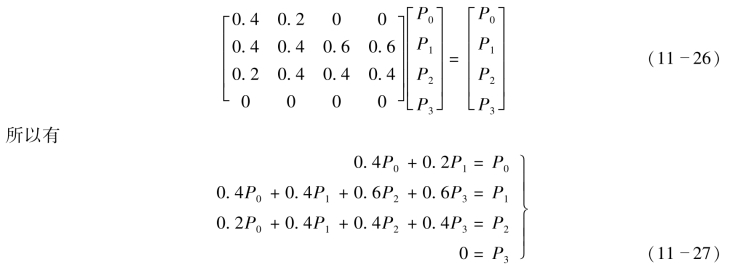
因为这四个方程式是不独立的,故要求解此四个未知数尚需增加一个条件
![]()
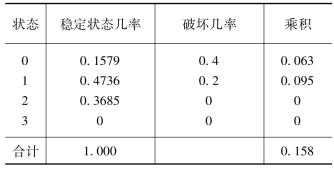
解得 P0=0.1579,P1=0.4736,P2=0.3685,P3=0,与前一方法结果相同。
这一方法也就是国内某些文献中所说的概率演算法。
5.计算水库供水保证率
由于水库供水破坏的几率只与年初水库所处状态有关,而稳定的水库状态概率代表水库正常运行时,年末(初)水库蓄水情况,故只要前面计算步骤中3、4两步结果相乘即得正常供水遭受破坏的几率。如表11-7所示,水库供水破坏几率为0.158(按年计)。同理可得按月计的破坏几率为0.0239。
本法的优点:
(1)本法的基本思路与第七节之三的库位频率法是类似的,但本法不必把总库容划分为年和多年库容。
(2)可以计入需水量、损失水量随时间和水库蓄水量的变化及考虑水库操作方式。
(3)计算的起讫时刻可以任意选择,不一定要按水利年度。这对于相期不明显或不稳定的河流带来很大方便。
本法的缺点:
(1)计算工作量大,当库蓄状态分段数较多时,需要借助电子计算机。
(2)只适用于年径流间是相互独立的。
表11-7 水库供水破坏几率(按年计)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




