如何利用合成总库容法实现多年调节？

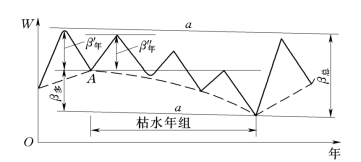
图11-15　多年调节总库容的组成

由图11-15可见，总库容可以分成两大部分——年库容β年和多年库容β多。多年库容的作用是拦蓄丰水年的多余水量，以补充枯水年的年水量不足，所以多年库容的计算是以一年为一个计算时段来进行水量平衡。如图11-15中虚线所表示的来水量。多年库容的大小只与年需水量和年来水量大小及排列次序有关。但实际上一年之内需水量及来水量还具有季节性的变化，年库容的作用就是为了均衡季节性变化。

下面分别讨论β多和β年的计算方法及这两部分库容的组合。

一、克—曼（克利茨基和曼凯里）第二法计算多年库容

设已知年径流之频率曲线（即已知Q0，Cv，Cs），多年库容β及年需水量α，欲求水库供水之保证率P。

先研究年径流相互独立的情况。多年中河川每年之来水可以用一根频率曲线来表示。有些年份来水特别枯，例如当k＜α-β，这种枯水年来临时，即使年初水库为蓄满，也不能保证该年用水需要。这些年称为绝对缺水年或绝对断水年，其多年中出现的几率为S1=1-Pα-β（见图11-16）。

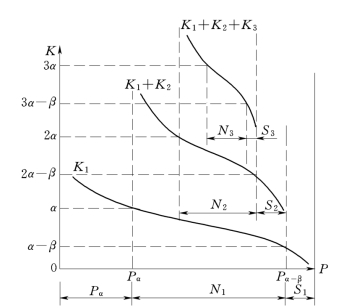
图11-16　克—曼第二法计算示意图

另一些年来水k≥α，则不论年初水库是满或空，均能保证正常供水，故称为绝对足水年，其出现几率为Pα。其余年α＞k＞α-β为中等水量年，这些年份之正常供水量是否会破坏，需视年初水库蓄水情况而定，而年初蓄水情况又与前一年来水丰枯有关。若遇到前一年为丰水年，那么到该年年初水库可能有较多的蓄水而保证该年正常供水；反之，若遇到前一年为枯水年，那么该年年初水库蓄水不多，就不能保证该年正常供水。所以这些年份称为条件断水年，其出现几率为N1。

至此，可以得出一个结论，在给定的多年库容β和年需水量α的情况下，水库正常供水的保证率一定在Pα和Pα-β之间。这显然不是最后答案，因为Pα与Pα-β之间的区间N1太大了。

为了进一步缩小这个不确定区间，就需要分析这些条件断水年中有那些年与前一年枯水年相逢时会断水。为此需作N1中之一年与前一年相加的二年来水量之和的频率曲线，即求N1这段频率曲线与天然年径流频率曲线之和的组合频率曲线（图11-16中之k1+k2），这条曲线的宽度只有N1。再来对这些条件断水年研究连续两年的水量平衡，两年总来水量为k1+k2，两年总用水量为2α，如果

那么即使两年前水库是蓄满的话，也不能保证后两年的正常供水，故为绝对断水年，其发生几率为S2。而k1+k2≥2α的那些年份为绝对足水年；另外一部分2α＞k1+k2＞2α-β则为条件断水年；其发生几率为N2。

通过连续两年水量平衡分析，供水保证率估计的区域范围已缩小到N2。

用同样的方法，取N2这段频率曲线与再前一年来水频率曲线组合，得连续三年之水量平衡，又可将N2分成绝对断水年（其发生几率为S3），条件断水年（其发生几率为N3）及绝对足水年。依次类推，不确定区域越来越小，最后收缩到很小范围（精度允许范围）于是水库供水破坏几率为

或者水库供水保证率

利用克—曼二法可以解决已知来水、用水及多年库容求供水保证率。当问题是已知来水，用水及保证率P求所需多年库容时，问题的解法基本上仍一样。不过此时需假定n个不同的多年库容值β，求出相应的供水保证率P，然后绘制β和P之关系曲线，再由设计的P值查出所对应的多年库容值，也就是说用试算内插的办法求解。

上面假定河川年径流量间相互独立无相关关系。但是某些河流的资料中出现的连续枯水年组，说明年径流量间有时存在一定的相关（r可达0.3～0.4），不考虑这点，便可能使所得库容偏小，处于不安全。

克—曼在发展其第二法的基础上，提出了分析法，其意图在于考虑相关影响及用分析法简化繁重的频率曲线组合计算。方法的要点在于，首先假定多年径流过程为马尔柯夫单链，其次以条件断水年之频率线段之中值代替全线，并使之与原径流频率曲线累加，然后通过数学推导，得出n+1年组的径流统计特征值kn+1，Cv，n+1，Cs，n+1的计算公式，公式应用方便，但因取中值之近似性，在α值较高时，可能有较大偏差。

在计算过程中考虑年径流序列之间的相关，会使得计算非常复杂。所以往往是先按年径流序列无相关来进行调节计算，然后再采用一些近似的办法，对计算成果作修正。一种修正的办法是增加库容来弥补由于忽略序列相关的影响；另一种是减小供水量来弥补这一影响。

二、线解图

由前所述，可见克—曼第二法计算相当冗长（主要为频率曲线相加之工作），故亟须应用图表，以便能简单地表示出在各种常用保证率下之β、α、Cv间的关系。对于来水服从P—Ⅲ型分布，且相互独立，Cs=2Cv之线解图，最早由普莱希可夫于1939年作成（见图11-17）。

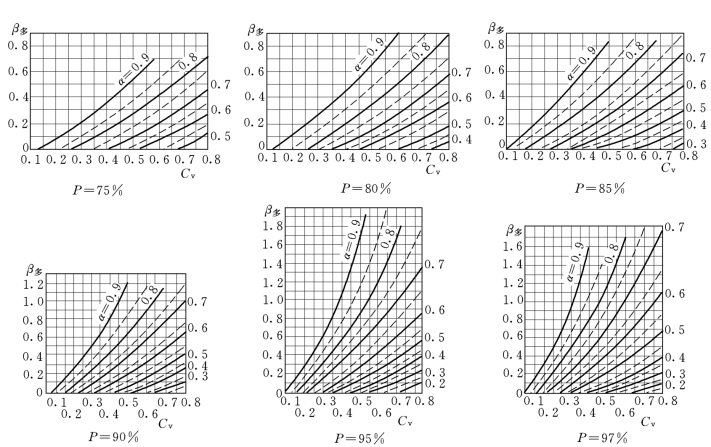
图11-17　求多年库容的普莱希可夫线解图

（Cs=2Cv，r=0）

如已知径流多年变化的统计特征值Cv，用水α及所需保证率P，则由相当之P的线解图，由Cv及α可查得β多，即为所需之多年库容。

如对于给定之P值并无造好的图，例如P=92%，则由相近之二图，即P=90%及95%，分别求得两个β多，再以直线内插法求相当于P=92%之库容。

同样，利用普莱希可夫图可由已给Cv、α、β求保证率P，或由Cv、β、P求供水量α。当Cs≠2Cv时，经过下列变数代换仍可用线解图。

当Cs＞2Cv时，要把原来的β、α和Cv换算成α′、β′和C′v后再查线解图

式中　α0——流量频率曲线中最小模比系数值，或设m为Cs与Cv之比值，则

例：已知Cv=0.3，Cs=3Cv，α=0.8，β=0.25，求P。

因为Cs≠2Cv，故先用式（11-22）和式（11-23）进行变数代换(www.xing528.com)

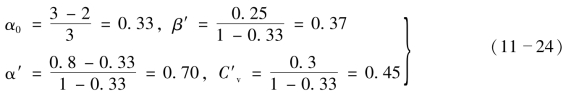
先在P=90%的图上，由C′v=0.45及Q′=0.70查得β=0.29，小于β′=0.37，故下一次查图时应选P=95%，根据同样的Cv′和α′，查得β=0.42，由直线内插求得供水保证率

1959年古戈里曾对Cs=2Cv，相关系数r=0.3的情况作出了类似的线解图。

年径流间相关关系（即序列相关）的存在，往往使连续枯水年组增长，所需多年调节库容也相应有所增大。因此，对于年径流序列相关比较明显的河流应考虑这一因素，不然会使所得库容偏小，偏于不安全。1969年斯瓦尼泽（CBAНИДЗе）等对年径流服从P—Ⅲ型分布（Cs=2Cv），及相邻年径流相关系数r=0～0.6，间隔0.1的情况，利用蒙特卡罗法生成2000年人工径流系列后进行调节计算，概括成新的、类似的多年调节线解图，可供在类似情况下参考查用。斯瓦尼泽等还同时给出了当Cs=1.5Cv及Cs=4Cv情况下，r=0.3时的线解图。

三、水库蓄水量频率法

克—曼第二法不足之处为仅能给出水库供水之保证率，而不能同时求出水库弃水水量与各种库位之频率。萨瓦林斯基进一步研究了每隔一定时段（例如一年）由于来水与用水结果，引起的水库蓄水量和水位的变化关系，而建议了水库蓄水量频率法（简称库位频率法），其要点如下。

设已知年初库位、年来水量及年需水量（包括损失），则由这些资料，根据水库水量平衡，足可定出到该年年末水库工作之可能情况，即年弃水量、不足水量及年终库位等。以第一年年末库位作为第二年年初的库位，同样进行水量平衡运算，即得第二年末的库位。以此类推，可得到多年工作情况，包括弃水、断水及各种库位的频率。应该注意：在调节过程中，从第二年起，年初库位不为一确定值，而为满和空之间各种可能水位的一条频率曲线。来水也不为一确定值，而是以流量频率曲线表示的各种可能来水量及其相对几率。故按水量平衡求年终库位时，必须应用频率曲线的组合。而所得的年终库位也为一条频率曲线，并非一个确定的数值。但由于年径流频率曲线在多年期中并不改变，年年相同，而需水也年年相同，故经过几年之数次运算后，库位频率曲线趋向稳定状态，即使继续运算也不改变其形状，这便称为稳定库位频率曲线，它表示在未来颇长的时期内，在所给来水与需水的条件下，水库的稳定工作条件特性，故可作为水库工作规划之依据。稳定库位频率曲线已与原始库位无关，故原始库位可任意选择。

作库位频率线的一般步骤如下（见图11-18）：

（1）任意假定一个年初蓄水量，如图11-18（a）所示。

（2）另作年来水频率曲线，如图11-18（b）所示，在同一图上作一需水α之横线，则横线以上正号表示余水量频率曲线，横线以下负号表示亏水量频率曲线。

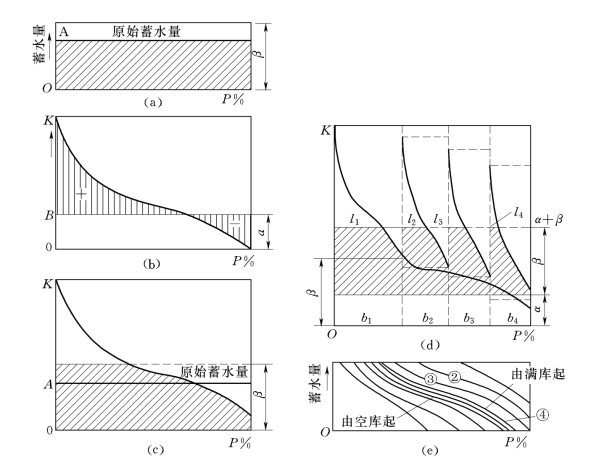
图11-18　库蓄水量频率法

（3）把图11-18（b）叠加于图11-18（a），使B点合于A点，得年终水库蓄水量频率曲线，如图11-18（c）所示。

（4）为求第二年年终之水库蓄水量频率线，先把上述（3）中所得作为本年初蓄水量频率曲线，并按面积不变及大致等高之间隔把此第二年初蓄水量频率曲线简化为几个阶梯，以表示不同的初蓄情况，如图11-18（d）所示。

（5）将天然来水频率线横向压缩为各分段阶梯之相应宽度，并分别迭置于阶梯形年初蓄水量上，则所得各分段曲线之纵坐标等于年初蓄水量和年来水量之总和。然后在图上划出α及α+β=横线。

（6）图11-18（d）中，在α+β线上诸截线l1，l2，l3，l4为水库蓄满后发生弃水之频率，α线以下诸截线为供水之保证率，而α与α+β之间阴影部分表示各种蓄水量之频率。

（7）把图11-18（d）阴影部分按横向总加之，则得一根曲线如图11-18（e）中②所示，此即为第二年末之水库蓄水量频率线。

（8）如此连续运算，可得相应的第三、第四年年终蓄水量频率线，如图11-18（e）中③、④线所示，这些曲线越来越密集，改变也愈来愈少。最后得出一稳定之蓄水量频率线，如图11-18（e）中粗线所示，其与上下水平线相交之两点分别表示多年运行弃水与供水之保证率。

稳定蓄水量频率线可由任意原始水位开始来求，如由满库开始，则曲线群由右向左渐趋极限之稳定位置；如由库空开始，则由左向右趋向同一极限，如图11-18（e）所示。

四、水库工作情况（水利要素）的频率曲线

研究水利设备的工作情况，在于作出各水利要素（如供水量、弃水量、缺水量、水库上下游水位等）的变化过程及其相应的持续曲线，以便于分析其各种数量与出现频率（或多年年平均持续时间）间的关系，明确水库和设备的多年工作情况等等。求水利要素的多年变化情况有时历法和数理统计法两类。

时历法已在第四节及图11-11中介绍过。数理统计法以上述蓄水量频率曲线法最为方便，在推求稳定的蓄水量频率曲线的同时，把图11-18（d）中α+β以上局部的组合频率曲线横向累加，得各种弃水量的频率曲线，把α以下的局部组合频率曲线用同样方法累加得缺水量频率曲线、如图11-19（a）阴影部分所示。

弃水频率曲线，缺水频率曲线及稳定的水库蓄水量频率曲线三者综合之，就可得调节后流量频率曲线，如图11-19（b）所示。综合的方法是：先在纵坐标为需水量α处作一水平线，然后把弃水量频率曲线迭加到该线上，这是因为水库蓄满情况下，水库下泄流量为需水量和弃水量之和。同理自需水量α这条水平线之右端减去缺水量频率曲线，因为这种情况下，水库实际下泄水量为需水量α与缺水量之差。

上述用库蓄水量频率法求多年弃水情况虽然方便，但较粗，因考虑调度等情况太简单。

五、年库容计算

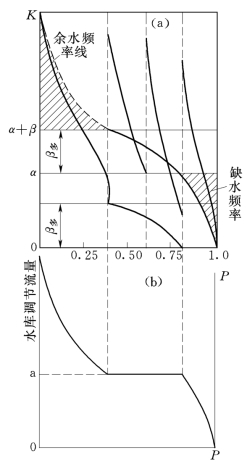
图11-19　水库调节流量频率线

多年库容的计算是以一年为一个计算时段，不计及年内来水与需水的变化。实际上，由于洪枯期径流季节变化的存在，仅多年库容是不够的。如前图11-18所示，如仅有多年库容，则在A时已蓄满，那么枯水年组第一年汛期余水量将无法再蓄，这就影响该年枯季用水的需要。从另一方面，也可以看作当仅有多年库容时，枯水年组前一年（丰水年）之枯水期的缺水将无法获得满足。因此，除了均衡年际间水量变化的多年库容外，还必须有均衡年内变化所需的年库容，这两部分组合起来才是所需要的总的调节库容。

由图11-15及上述讨论可见，多年调节水库中的年库容取决干枯水年组第一年（年来水量小于需水量）汛期之多余水量或枯水年组前一年丰水年（年来水量大于需水量）枯季缺水量。应该选择怎样的年份来确定这部分年库容呢？此典型年的选择原则如下：

（1）就年水量而论，如果从枯水年组第一年的汛期余水量来看，一般说来，汛期余水量大小与年水量大小有关，年水量越大，汛期余水量越大，要求年库容越大，为安全起见，不宜使年库容选得太小，所以应选取典型年年水量尽可能大些。但由于已是枯水年，所以其年水量最大不应超过年需水量。再从枯水年组前一年的枯季缺水量来看，年水量越小，枯季缺水量越多，要求年库容越大。为安全起见，应选取典型年年水量尽可能小些。但由于是丰水年，其年水量最小不应小于年需水量，否则不属于丰水年了。综合上述两方面的考虑，应选取年来水量刚好等于年需水量的那些年份作为典型年较为安全，因为这些年份要求的年库容较大。

（2）年内分配可取多年平均分配比例之过程图。这是因为极限枯水年组出现机会不多，其第一年遇到来水与需水很接近的年份机会较少，而这一年的年内分配又是极不利，这样的机会极为稀遇，所以不予考虑。

对选出的典型年用前述之列表法，图解法或简化水量平衡公式法进行调节计算，可求得多年调节的年库容β年。

多年调节水库的总库容为β总=β多+β年

将总库容人为地划分为多年和年库容两部分，虽然给计算带来诸多好处和方便，而且似乎在多年库容计算中，来水、需水、库容和保证率这四者之间的关系比较明确，严格。但是对于总库容而言，这四者之间的关系是否仍然保持不变呢？也就是说，总库容放空的几率是否就等于多年库容调节计算中多年库容的放空几率呢？显然无法得出肯定的结论，因为在实际水库运用中，总库容并不是按硬性划分年库容与多年库容来起调节径流作用的。

为了克服把总库容硬性划分为年库容和多年库容这一缺陷，除了下面将要介绍的直接总库容法外，在如何把年库容与多年库容合理组合，使得总库容的放空几率能等于设计保证率方面，曾有人提出了一些改进。