时历法多年调节计算方法详解

由水量平衡原理可知，当年需水量小于设计保证率所相应的年来水量时，水库不必跨年度蓄水，只需蓄当年汛期一部分余水量就能够补充枯水期之不足，这样的水库就是年（季）调节水库。当需水量提高到刚好等于设计枯水年来水量时，或者需水量不变而设计保证率提高到设计枯水年来水量与需水量相等时，那么应该把设计枯水年汛期多余的水量全部蓄起来刚好补充枯水期之不足，水库无多余的弃水，这时称该水库为完全年调节水库。如果需水量或设计保证率再提高，以至于设计枯水年总来水量已小于年需水量，要满足正常供水，单纯依靠水量的年内调节已不可能，必须跨年度调节水量，把丰水年多余的水量蓄起来，以补充少水年水量之不足，这就需要多年调节。

多年调节水库往往要经过若干个连续丰水年才能蓄满，经过若干个连续枯水年才能使水库放空，因此完成一次蓄泄循环往往需要好几年。多年调节水库的库容或保证供水量取决于连续枯水年组的总亏水量。因此，用时历法进行多年调节计算时，所需要的水文资料远较年调节时为长，一般应在30年以上，且足够代表多年变化的典型，否则，所得结果不可靠。

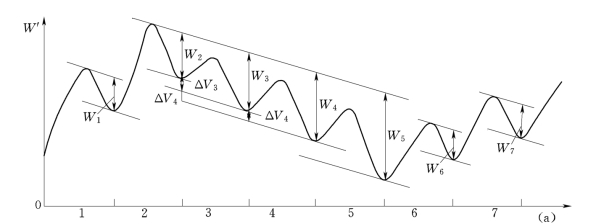
设多年系列的径流差积曲线已绘出（图11-10仅列出一部分）。在图上作已知调节流量的斜切线，则各年保证调节流量所需的相应库容为W1、W2、W3、…。图中第1、2、6、7年来水量大于调节流量，故仅需当年汛期蓄水即可解决。第3、4、5年诸年来水量均小于保证调节流量，故各年均需前一年留水补充。例如就第三年来说，须第二年末留ΔV3的水量，如果要保证第4年也正常供水，那么需在第三年末留有ΔV4的水量，也就是说，要在第2年末留有ΔV3+ΔV4的水量。由此可见，多年调节所需的容积不仅与各年来水情况有关，而且与各年间来水的配合情况有关。

与年调节时一样，根据上面求得之W1、W2、W3、…诸值，按经验频率公式进行统计，作出如图11-9（a）那样的V—P关系曲线，由需水保证率P可查得相应的设计库容V（如图11-10所示）。

(www.xing528.com)

图11-10　差积曲线法进行多年调节计算

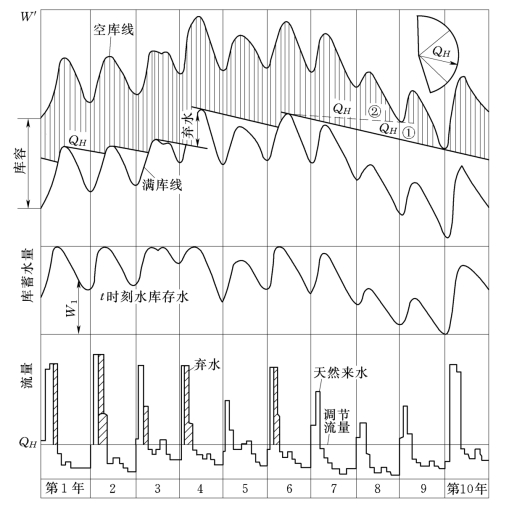
图11-11　多年调节水库工作图

同样，可以解决已知库容求调节流量。图11-11所示为已知库容的多年径流系列的差积曲线的一部分，把多年来水差积曲线上下移动一段距离刚好等于给定的库容。由曲线可知，最缺水的枯水年组之一为第6年到第9年，同时找出其他比较严重的枯水年组（图中未绘出），在这些枯水年中，各作最大公切线，即表示该年组中的最大均匀调节流量。诸枯水年组中相应于最小的调节流量，比如说第6年到第9年的年组为最不利的枯水年组，其调节流量QH为最小，那么相应于此调节流量的保证率近似地等于P=n/（n+1）；n为径流系列的年数。如果n年中允许破坏一年，那么供水破坏年份必定是最不利的枯水年组之最末一年，对本例而言为第9年。因此除去第9年外，再作公切线得新的调节流量QH。然后，把此QH与其他枯水年组之调节流量比较，取最枯者作为保证率为P=（n-1）/（n+1）时之调节流量。依次类推，可作出如图11-9（b）那样的QH—P关系曲线，根据需水设计保证率从关系曲线上查得相应的调节流量。求得调节流量QH后，可作其他年份之调节（图11-11）。由图可见，即使在多年调节中，弃水仍不可免，而水库在多数年份供水季末均蓄至正常蓄水位，仅在第5及7～9年水库起了多年调节作用。同时，水库也并非每年放空，仅枯水年组末水库才放空。

在多年调节水库中，由于库容较大，水量损失有时颇为可观。计及损失之法（如年调节）。简单考虑可近似地取设计枯水年组水库平均库位来估计各种损失水量，然后从调节流量QH中扣去损失流量得净调节流量；或者把这部分损失水量加到库容上去，使库容增大以抵消此部分水量之损失。