上一节我们已解决了在特定的来水情况下,调节流量与所需库容之间的关系。但由于天然来水量每年不同,一年内径流分配也多种多样,因此即使需水量每年固定不变,所需要的调节库容也是每年变化的。那么水库到底应修多大才合适呢?或者,在库容已定的情况下,由于每年来水量和年内分配不同,它所能提供的调节流量也是不同的,那么该水库到底能提供给多大的调节流量呢?这就是本节所要解决的课题。解决这一课题有两个途径:长系列操作法及典型年法。
一、长系列操作法
假定有N年来水资料,用第三节所讲的三种方法中的任何一种,可以对每一年来水资料,根据给定的需水(例如QH1)来计算调节库容,或反之根据调节库容来计算调节流量,因此可得到N个调节库容或调节流量。把此N个调节库容或调节流量看成是随机变量,用经验频率公式p=m/(n+1)绘成调节库容或调节流量频率曲线,见图11-9(a)、(b)之拟合实线。
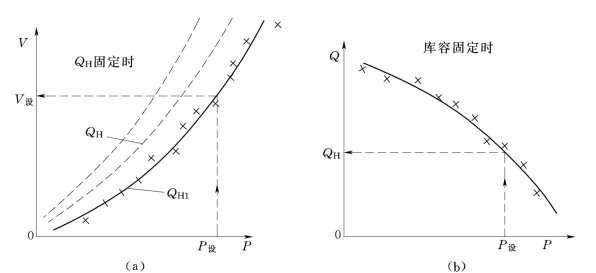
图11-9 调节库容或调节流量与保证率的关系
(a)V—P关系曲线;(b)Q—P关系曲线
图11-9(a)表示在需水固定情况下,调节库容与保证率之间的关系;且需水增加时,关系曲线也不同(图中虚曲线),而图11-9(b)表示在库容一定情况下,调节流量与保证率之间的关系。根据需水的设计保证率P设可以由图11-9查得相应的设计库容V设或保证的调节流量Q调。因为根据此V设来修建水库,在今后长期运行中有P设这些年份为了保证正常供水所需要的库容小于或等于V设。也就是说对这些年份而言,亏水期实际亏水量小于水库所能提供的水量,因此这些年份肯定能保证正常供水而不遭受破坏。相反,还有(1-P设)这些年份,来水很枯或年内分配很不利,为了保证正常供水所需的库容大于V设。也就是说,对这些特殊年份,亏水期实际亏水量超过水库所能提供的水量,因此这些年份肯定不能保证正常供水。如果实测资料(样本)能很好地代表总体的话,那么从长期运行角度来看,这样求得的V设使正常供水得到保证的年数刚好等于设计保证率。
用相同的方法可以分析图11-9(b)所求得的调节流量一定也与设计保证率相符。
由此可见,长系列操作法所求得的参数(即设计库容或保证供水量)其设计保证率概念比较明确,所以凡条件许可均应按长系列操作法来确定参数。但是在下面两种情况下可采用较简单的设计典型年法。第一种情况是无资料地区,或资料不足时,无法采用长系列操作法,一般中小水库常会遇到这种情况。
第二种情况是精度上要求不高,例如初步规划阶段,需要从大量方案中选几个可能的方案再进行详算。此时主要任务是选方案而不是确定参数。为了简化计算同时又不影响方案之间相对优劣的比较,常采用下节所介绍的典型年法。
二、典型年法
典型年法的要点是选择一个来水过程线,作为设计典型年,根据此设计典型年计算库容或调节流量作为设计值。典型年法的关键是设计典型年的推求。推求设计典型年过程线的方法有两种,一种是同倍比法,另一种是同频率法。
1.典型年同倍比放大法(简称同倍比法)
常用的有两种同倍比放大法:一种是以年水量为控制;另一种是以水库供水期水量为控制。对于年水量控制的第一种方法和步骤如下:
(1)先对坝址断面的年径流资料进行统计分析,确定其线型及三个统计参数Q0、Cv、Cs。
(2)由年径流统计参数计算相应于需水保证率的年径流量Qp。
(3)从实测资料中选择年径流量与Qp接近且年内分配有代表性的一年或几年作为典型年,其年平均流量为Q典。
(4)计算缩放倍比K=Qp/Q典,再用此K值遍乘该典型年实测各月平均流量,得设计典型年。(https://www.xing528.com)
(5)对所推求的设计典型年进行调节计算,求得调节库容或调节流量。当所取设计典型年不止一个时,为安全起见,可选偏不利者作为设计值。
上述年水量控制法,其基本假定是调节库容或调节流量,主要取决于年来水量。这个假定,没有着重考虑年内分配的重要影响。因此,只在年内分配各年一致或变化不大的河流才接近正确,其年水量的保证率也才与库容或调节流量的保证率一致。
为了改进以年水量控制选典型年的缺点,比较合理的是以供水期水量控制同倍比典型年法。因为水库库容决定于供水期的亏水量,即
![]()
当供水期历时T供历年不变时,调节库容完全取决于供水期天然径流量。在这种情况下,我们只要分析亏水期水量的频率曲线,再根据需水设计保证率计算其相应的设计供水期天然来水量Wp,然后从实测资料中选择供水期水量W典接近Wp者作为典型季(年),用K=Wp/W典遍乘所选典型季(年)各月流量得设计典型季(年)。
此法的缺陷是,实际上T供非常数,因此决定T供也不简单,影响此法理论上的严密性。因为库容或调节流量决定于两个因素,供水期历时T供和供水期来水量W供,无法严格地概化成一个变量。在实用上只好根据大多数较枯年份的T供历时作为设计值。
2.典型年同频率放大法(简称同频率法)
为了克服同倍比两法中的缺点,故提出同频率法。
同频率法的精神是拟定一条设计年流量过程线,而该过程线各种长短时段的水量都符合指定频率。同频率法具体计算步骤如下:
(l)根据实测资料,统计每年最枯1个月水量W1,连续最枯2个月水量W2…,直到连续最枯11个月水量W11及年水量W年,并对上述各种时段水量进行频率计算,求得各种时段设计频率的水量W1p、W2p、W3p、…、W11p及W年p。为了减少计算工作量,一般并不需要每个时段都作频率计算,而是根据需要选择几个时段,例如可选取W2p,W4p,W6p及W年p。
(2)从实测资料中选择各时段水量都较接近设计值的一年为典型年,其2个月、4个月、6个月及年水量分别为W2典、W4典、W6典及W年典。
(3)按倍比K2=W2p/W2典来缩放典型年中最枯连续两个月的水量,按k2-4=(W4p-W2p)/(W4典-W2典)来缩放连续最枯4个月中的另外2个月。依次类推,可推求得同频率设计年典型过程线。
(4)对此同频率设计典型过程线进行调节计算,得设计库容或保证的调节流量。
同频率法与同倍比法基本假定一样,都是基于某一时段来水量与库容之间呈单调函数关系。不同之处在于同频率法控制时段较多,可克服同倍比法因时段选取不当或典型年选取不当而产生的误差。
三、库容、调节流量与设计保证率三者之间的关系
上面主要是针对设计保证率P已选定情况下,如何根据需水量来计算设计库容,或根据库容来计算可以保证的供水量。但是,在规划设计中更经常遇到的问题是:水库的最高蓄水位即库容没有预先给定,水库所负担的供水供电任务也不是已固定不变。若水库修建得大一些,则水库的调节流量大,水头高,可以多发电,多灌溉。但水库的工程投资大,淹没损失大,这就需要通过效益和投资费用比较选择最优方案。
所以,径流调节计算的最一般的任务是:在来水确定的情况下,计算库容、保证供水量和设计保证率三者之间的关系,为选择水利规划方案提供数据。
由前面介绍的已知调节流量,用长系列操作法或典型年法可求得不同设计保证率P与设计库容的关系,见图11-9(a)。若取不同的调节流量,用同样方法求得其相应的V—P关系曲线,并把它综合在一起,就可得到以QH(调节流量)为参数的V—P—QH三者关系图。这种以等差QH为参数的曲线群,看图11-9(a)诸曲线,因一般随QH增加,T供亦常增长,故愈向右上,曲线间间距愈发散。这说明库容增值所引起的效益增值是逐渐减小的,而所引起的投资增加却是递增的。所以其中必然存在着一个较为经济合理的库容和需水量的配合方案。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




