年调节水库的调节流量与有效库容关系分析

一般说来，径流调节计算的任务，在已知天然来水的条件下，不外两类：一类是根据用水部门要求的调节流量决定水库所需有效库容；第二类是已定水库有效库容，要求解可提供的调节流量。

在已知来水条件下，一般可用列表法，差积曲线图解法或简化水量平衡方程式这三种计算方法来求解上述两类课题，或一般地确定调节流量和调节库容之间的关系，现分别介绍如下。

一、列表法调节计算

列表法调节计算它能较严格和细致地考虑调节流量及各种损失水量随时间及随水库蓄水量的变化。所以它是一种最通用的方法。

设用水部门需水流量即水库调节流量为已知（见表11-1第3栏），该年的天然入库流量列于表11-1之第2栏。表中第1栏为月份。在水利计算中一般不常用日历年，而是采用水利年，即以水库蓄泄过程循环作为一年的起讫点，取水库开始蓄水作为一年的起点。本例采用3月至次年×月作为水利年来进行调节计算。把一年划分为12个计算时段，每个计算时段ΔT为一个月。由于月份不同，天数也不同，所以每个计算时段的实际秒数也不同，在列表法调节计算时可以细致地考虑这一点。但在实用上，ΔT一般采用常数，取平均值ΔT=30.4d=2626560s。由于ΔT为固定常数，所以在水利计算中常采用流量×时段这种单位来表示水量，例如，前章所说的（m3/s）.月或（m3/s）.日。而

用这样一种单位，可以大大简化调节计算。

表11-1中的第4栏和第5栏，分别表示各月的余、亏水量，为来水量与用水量的差值。本例以9月份至次年3月份为亏水期，六个月总亏水量为89.1（m3/s）.月，即2.34亿m3。而3月至8月为余水期，6个月总余水量为190.9（m3/s）.月。余水期多余的水量远远超过亏水期不足之水量。余水期的余水量没有必要全部蓄在水库中，蓄水多少取决亏水期所缺水量。也就是说，为了保证全年各月25.0m3/s的用水流量，水库在亏水期必须补充放水89.1（m3/s）.月，所以余水期只需蓄89.1（m3/s）.月即可，此数据即为该年所需库容。

表11-1　列表法年调节计算

显然，年来水量401.8（m3/s）.月，应等于该年用水量加上弃水量之和300+101.8=401.8（m3/s）.月。这也可作为列表计算有否错误的一个校核。

求得水库调节库容后，根据拟定的水库运行方式，可得出水库各月的蓄水量变化情况（第6栏）及水库弃水情况（第7栏）。本例采用最简单的操作方式：即水库有余水就蓄，蓄满后还有水多就弃（可称为早蓄方式）。

图11-3表示该年来水、用水、弃水及水库蓄水量变化情况。水库从3月初库空开始蓄水，到6月上旬水库蓄满。由于6月中、下旬及7、8两个月来水仍超过用水需要，因此多余的水量被迫废弃，而水库仍保持满库状态。9月开始进入供水期，水库蓄水量不断下降，一直到2月底水库放空，完成一个循环。

本例比较简单，一年中只有一个余水期和一个亏水期，称为一回运用。由于来水和需水在年内分配不同，一年内可能有若干个余水期和亏水期。例如图11-4（a）、（b）为两回运用的情况，分别有两个余水期（其余水量为ΔV1、ΔV3），及两个亏水期（亏水量为ΔV2、ΔV4）。图11-4（a）中余水量ΔV3大于其前面亏水量ΔV2，因此这一年中虽有两个亏水期，但每个亏水期开始时刻水库均能保证蓄满，故所需调节库容取决于两个亏水期中亏水量较大者，本例V=ΔV4。而图11-4（b）由于余水量ΔV3小于其前面亏水期亏水量，因此第二个亏水期来临时水库不可能是蓄满的，故所需调节库容V=ΔV2+ΔV4-ΔV3。

由此可见，调节库容大小不仅与相邻的余亏水量有关，而且还与余水期的数目及排列次序有关。为了帮助确定多回运用水库之库容，可绘制来水量与用水量逐月差值的累积曲线，如图11-4最下面二图所示，取该累积曲线之最高点M与其右边的最低点N之间垂直距离即为所需之调节库容。

图11-3　水库的一回运用

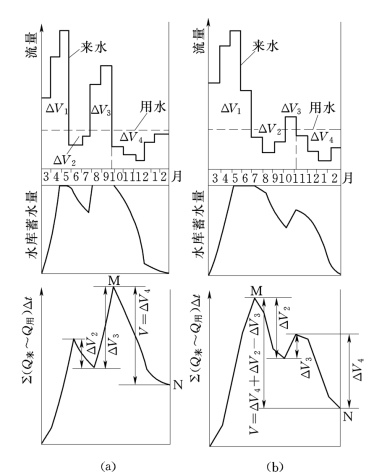
图11-4　水库的多回运用

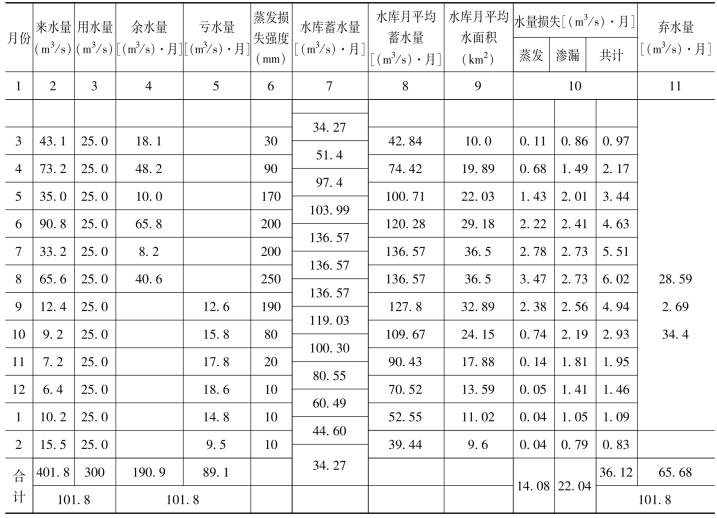
考虑损失之调节计算：水库在对来水进行调节以满足需水要求时，不可避免地会产生各种各样的水量损失。因此水库库容应酌情增大，以抵偿此部分耗水，保证正常供水。由于水量损失（如蒸发、渗漏等）往往都与水库蓄水位有关，所以在调节计算时常需试算。设来水及用水仍同上例，考虑水量损失后列表计算如表11-2所示。

表中第1～5栏同表11-1。本表系用试算法进行水量平衡计算，步骤如下：

（1）从2月底库空开始，即从死库容34.27（m3/s）.月开始逆时序进行水量平衡计算。故表11-2第7栏之最初及最末行数字即为死库容。

（2）先假定2月初水库之蓄水量值为44.60（m3/s）.月，填在表11-2第7栏倒数第2行中。

（3）计算水库月平均蓄水量39.44（m3/s）.月及相应之水库水面积9.6km3分别填在表中之第8、9栏相应位置。

表11-2　考虑损失之列表法年调节计算

（4）蒸发损失等于该月蒸发损失强度乘以该月水库平均水面积，再除以一个月的秒数，得用（m3/s）.月表示的蒸发损失量，即

填在第10栏相应位置。

（5）水库渗漏损失根据库区地质情况，取月平均水库蓄水量之2%，即

填在第10栏相应位置。

（6）由本时段水量平衡计算，求时段初（即2月初）水库蓄水量，即

它与原来假定值相符，试算结束转入上一时段1月份水量平衡计算。

若计算结果与假定值不符，则应重新假定时段初水库蓄水量重算。

（7）依次类推，一直计算到供水期开始时刻9月初水库蓄水量为136.57（m3/s）.月，此即为所求之水库库容。

（8）求得库容后，再从蓄水期开始时刻3月初死库容顺序用同样方法进行逐时段水量平衡计算，到6月底水库已可蓄满并还有多余水量废弃。

考虑水量损失后，所需之有效库容（即调节库容）为136.57-34.27=102.3（m3/s）.月，比不计损失时库容增大了13.2（m3/s）.月。此增大的库容值等于供水期9月到次年2月的损失水量。至于蓄水期3月到8月期间的水量损失值对库容无影响，只不过减少了水库的无益弃水。在不计损失时总弃水量为101.8（m3/s）.月，而考虑损失后总弃水量为65.68（m3/s）.月，这部分减少的弃水量等于该年所损失之水量36.12（m3/s）.月。

由于水量损失本身不大且扣损指标也是一个粗略的估计数据，所以在实用上一般不需采用如此麻烦的迭代试算，而可用一些较简单的方法来估计水量损失。例如，方法之一是，先按不计损失进行调节计算，求得各月之平均库蓄水量，并按此平均蓄水量来计算水量损失。然后从各月天然来水中扣去此损失水量，再进行一次调节计算。还可以有另一些简算方法，可自行思考。对于水量损失占来水比重较大的地区，例如西北干旱地区的蒸发损失及灰岩地区的渗漏损失都较大，则不宜采用上述简单的方法来估计水量损失。

二、图解法调节计算

天然径流和需水的时历变化过程，可以有两种图示方式：一种是直接以流量本身的逐时变化Q—t来表示的，如熟知的流量和需水过程线，上一节列表法调节计算中来水及需水的时历变化，也是采用这种方式表示的；另一种则是从某一原始时刻算起到各时刻的累积水量变化曲线的形式来表示。

这种流量累积曲线W=f（t），是以水量W为纵坐标，时间T为横坐标，如图11-5（b）所示。它是流量过程线的积分曲线，两者之关系为

累积曲线的每一纵坐标表示从计算开始时刻到所给时刻这一段时间内流经所研究断面水量之和。作图的开始时刻可取流量资料的开始日期或计算年限的开始时刻。

累积曲线就如一个仅有入流而无出流的水库蓄水量逐渐增长的过程。(www.xing528.com)

为作图及计算方便起见，流量累积曲线的纵坐标常采用流量.时段单位来表示。例如在年或多年调节计算时，计算时段取一个月，那么纵坐标应采用（m3/s）.月。对日调节，计算时段取一小时，那么纵坐标采用（m3/s）.时。这种表示方法的好处在于，流量累积曲线各时刻的纵坐标就等于从开始时刻到该时刻为止的全计算时段平均流量的累积值。

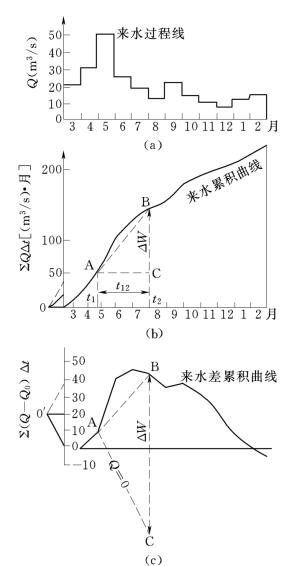
图11-5　累积曲线图解法示意

累积曲线上任二点A、B之纵坐标差ΔW（见图11-5），表示在t1、t2时段内流过的水量。割线AB之斜率与t12时段平均流量呈正比，可通过流量比尺直接读出其平均流量值。

流量比尺的绘制很简单，沿横坐标轴，在坐标原点左边一个计算时段的长度处取一点0作为流量比尺原点。通过0点的任意直线在纵坐标的截距读数，即为该直线斜率所代表的流量值。

由于累积曲线的特点，所以在整个时间内该曲线都是不断地上升。因此在绘制较长期的多年的径流累积曲线图时，为避免绘出的图太大，就必须选择很小的水量比尺，但这样又降低了精度。利用差额累积曲线（见图11-5下）可避免这个缺陷。相对于差额累积曲线而言，上面所说的就称常（或正）累积曲线。差额累积曲线也简称差积曲线。

从流量过程线上减去一常数流量值，例如Q0，然后把各单位时段的差量Q-Q0累积之，则得差累积曲线的各纵标值，即

流量Q0通常采用接近于所研究时期内的平均流量（一般取整数），故曲线形状呈以水平线为中心的波形曲线。

差累积曲线也有如常累积曲线所具有之特性，但有下面几点差别：

（1）曲线（图11-5则为连续折线）不仅有上升，当Q＜Q0时，曲线下降。

（2）曲线上任两点纵坐标差，等于此时段内流过之水量减去Q0流量在同一时段内流过之水量。

（3）由式（11-4）可知dw′/dt=Q-Q0，故差累积曲线上切线（图11-5则为各折线）斜率与流量差Q-Q0成比例。

把常累积曲线的流量比尺原点向上提高一段距离等于Q0，得差累积曲线的流量比尺原点0′（见图11-5）。由0′就可作出差积曲线的流量比尺。

利用常累积曲线及差积曲线进行水库的图解调节计算是很方便的。现仍以表11-l所列之来水及用水资料为例，其常累积曲线如图11-6所示，用图解法求库容的步骤如下：

（1）平行移动需水累积曲线，使来水累积曲线切于M点。

（2）再平行移动需水累积曲线，使与来水累积曲线切于M点之右下方N点。

（3）两切线之间的垂直距离即为所需之调节库容V。

上切点M为余水期到亏水期之分界点，在M点以左，来水累积曲线之斜率大于需水累积曲线之斜率。根据累积曲线之特性，斜率之大小即表示流量之大小，所以M点以左为来水流量大于需水流量，故为余水期。而M点以右则相反，来水累积曲线之斜率小于需水累积曲线之斜率，因而是亏水期。同理，N点是一个亏水期过渡到余水期之分界点，N点以左是亏水期，而N点以右是余水期，因此M、N两切点之间表示来水小于需水之亏水期。M点为供水期开始时刻，而N点则表示供水终了时刻。

图11-6　利用常累积曲线求库容

由累积曲线特性可知，供水期tM～tN这一时段天然来水总量为RN，而相应的需水累积量为SN，故亏水量为RS，它也即为所需之调节库容V。

如果水库在蓄水期的操作方式仍同前列表法，那么到了A点来水累积曲线与需水累积曲线之间的垂直距离刚好等于调节库容V，表示水库已蓄满，其后一直到tM时刻水库保持蓄满状态。图11-6中阴影部分表示水库各时刻之蓄水量，而AB线以上与来水累积曲线之间的垂直距离表示累积弃水量，这一年总弃水量即为MB。

这里必须再强调一下，调节库容取决于左上切点与其后续之右下切点之间的垂直距离。而决非左下切点与其后续之右上切点（图11-6之0、M点），因为后两点之间并非是亏水期而是余水期，所以该切点之间的垂直距离乃表示余水期总余水量。

图11-7为用差累积曲线表示之来水与需水。仍取用表11-1资料，Q0采用33m3/s，OE方向为斜坐标轴，其斜率表示Q=0。由于该年需水量为25m3/s，小于Q0，故需水之差累积曲线之斜率为负的。图解法同上。

在实际计算中，由于差积曲线之上切点位置比较显著，故作图时常省去上切线。

图解法对多回运用调节计算特别方便，因为不必去考虑水库是几回运用的，以及余亏水量的大小与排列次序等。一律用相同的方法去寻找最高切点及其后续的右下切点。图11-4（b）即为用差积曲线法计算多回运用情况下的调节库容。

另外，当解决另一类问题，即已知库容求最大可能之调节流量时，用图解法较列表法更为方便。

例如，已给库容V，求最大可能之均匀供水。在此种情况下，由于需水累积曲线尚未知，因此先平行移动来水累积曲线，使两平行之来水累积曲线之间的垂直距离刚好等于已给定的库容V。在二来水累积曲线之间作一公切线（先切下线，后切上线），此公切线之斜率即表示所求之最大可能均匀调节流量（见图11-8）。在这种情况下，满库点M在下方，空库点N在上方，故上曲线可称为空库线。当用水线与其相合时，表示库空，故调节流量不应与此线交叉。下曲线称满库线，当用水线与其相交而穿过时，即表示有弃水。

图解法也可近似地考虑水量损失。可先初估各时刻平均库位，求得各种水量损失后，自来水累积曲线中减去之，即把水量损失视作为天然来水的减少部分。

图11-8　已知库容之图解法

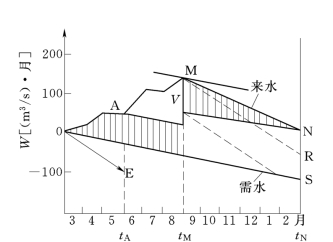
图11-7　差累积曲线求库容

三、用简化水量平衡方程式进行调节计算

上面已说过，径流调节计算的基本原理和方法是把整个调节周期划分成若干个计算时段，然后逐时段进行水量平衡求得水库蓄泄过程。如果我们把整个调节周期只划分成两个计算时段——蓄水期及供水期进行水量平衡计算，这就是本节所要介绍的简化水量平衡方程式调节计算方法。

由前述已知，水库调节库容取决于亏水期之最大累积亏水量，即

式中　T供——供水期历时；

　　　W供——供水期天然来水量。

当调节流量已知时，利用式（11-5）可确定调节库容V。反之，当已知调节库容V，可利用该式来计算调节流量Q调

用这个方法进行调节计算虽很方便，但必须注意两个问题。第一，供水期T供的确定是否正确，特别是在多回运用时或已知库容求调节流量时，T供往往要由试算确定。第二，必须检验一下蓄水期末水库是否能保证蓄满，即下面不等式应成立

式中　W蓄——蓄水期天然来水总量。

当要计及水量损失时，可由供水期平均蓄水量来估计供水期水量损失ΔV供，蓄水期水量损失ΔV蓄亦同，然后从式（11-5）、式（11-6）、式（11-7）之来水项中减去之即可。