控制测量：平面与高程的测量方法分析

一、控制测量的概念

为了防止误差累积和便于分幅进行测图，在碎部测量前应以较精密的仪器和观测方法，先在测区内测定少数控制点，建立统一的平面和高程控制系统。这些控制点互相联系形成网络，称为控制网。根据控制网的测定精度不同，可以分为基本控制网和图根控制网；后者是在前者的基础上补充加密而来，精度比前者低。基本控制网按其作用又分平面控制网和高程控制网，二者所用的测量仪器和测量方法完全不同，布点方案也有不同的要求。专门测设平面控制网的工作称为平面控制测量，专门测设高程控制网的工作称为高程控制测量。

下面简略介绍国家基本控制网和图根控制网的布设方法。

（一）国家基本控制网

国家测绘部门在全国范围内首先建立的平面控制网和高程控制网，是全国地形测量和施工测量的起始依据，称为国家基本控制网。

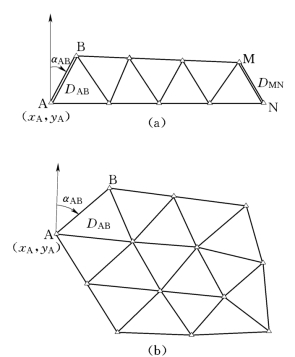
图7-2　三角锁和三角网

（a）三角锁；（b）三角网

1.平面控制网

国家平面控制网的建立有两种方法，即：三角测量和导线测量。在一般情况下主要采用三角测量，即按规范要求在地面选择一系列控制点，组成互相连接的三角形，观测所有三角形中的内角，并精确测定起始边（基线）的边长和方位角，按三角形的边角关系逐一推算其余边长和方位角，进而算出各点的坐标。如果这些三角形排列成条状，称为三角锁，如图7-2（a）所示；排列成网状，称为三角网，如图7-2（b）所示。构成三角锁、网的各三角形顶点称为三角点，也称大地点。各三角点都按规范要求在地面埋设标石表示点位，并架设觇标以供观测时照准之用（见图7-3）。我国三角测量分一、二、三、四等，一等精度最高，由高到低逐级控制，构成全国基本平面控制网。一等基本锁大致沿经纬线方向布设，边长20～25km；二等三角网布于一等锁环内，边长13km左右。三、四等三角点是二等三角网的进一步加密，其中三等三角形边长8km左右，四等三角形边长2～6km。

在通视比较困难的森林隐蔽地区，常用精密导线测量代替相应等级的三角测量。导线测量是将相邻控制点连接成一条折线（见图7-4），依次测定各折线边（导线边）的长度和转折角，根据起算数据推算出各边的坐标方位角，从而求出各导线点的坐标。

随着精密光电测距仪的广泛应用，我国平面控制测量的面貌发生了巨大变化：三角测量已由单纯测角逐渐发展到边角并测，形成边角网或测边网；控制点的测定方法不断改进和完善，点位测定精度越来越高了。

2.高程控制网

全国高程控制网主要采用水准测量方法建立，按控制次序和施测精度分为一、二、三、四等。施测各等水准点所经过的路线称为水准路线。一等水准路线是国家高程控制的骨干，也是研究地壳升降和其他有关科学问题的主要依据。二等水准路线是国家高程控制的全面基础；三、四等水准路线则直接为地形测图和工程建设提供必须的高程控制点。在各等水准路线上每隔一定距离埋设稳固的水准标石（即水准点，如图7-5所示），以标定所测高程点的位置，便于长期保存和使用。

图7-3　三角点的标志（异常标）

（二）图根控制网

国家基本控制点的密度远不能满足测绘地形图的需要，必须进一步加密，以保证测区各个部分都有一定数量的控制点能够用于测绘地形图。这些直接用于测图的控制点称为图根点。许多图根点互相联系形成图根网。图根点的密度要求与测图比例尺有关，一般规定如表7-3所示。

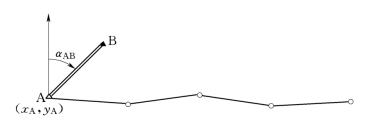
图7-4　导线测量

表7-3　图根点密度表

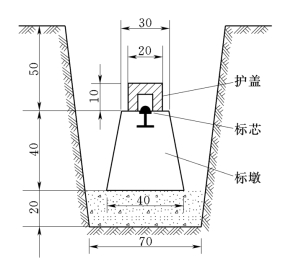
图7-5　水准标石（单位：cm）

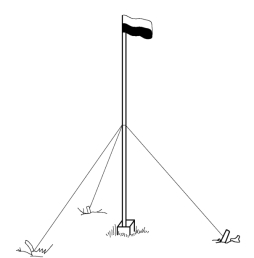
图7-6　图根点的标志

图根点的平面位置一般采用导线测量、小三角测量或经纬仪交会法进行测定；由图根点组成的这些图形应附合于高级控制点上。在无国家基本控制点的测区内，又不需与国家统一坐标发生联系时，可以布设独立图根控制网，采用假设坐标系统。图根点除了测定其平面位置外，还需用水准测量或三角高程测量的方法测定其高程，作为测绘地貌点、地物点的平面位置和高程的依据。

图根控制测量的特点是范围小，边较短，精度要求、施测和计算方法都不像国家基本控制那样严格。图根点的标志一般采用木桩或埋设简易混凝土标石，并用标旗作为觇标（见图7-6）。本章将重点讨论如何建立图根控制网问题。

二、经纬仪导线测量

（一）导线测量的外业工作

1.导线的布设形式和点位选择

经纬仪导线有三种布设形式，即：起迄于同一点的多边形闭合导线，如图7-7（a）所示；布设在两已知点间的折线形附合导线，如图7-7（b）所示；从一个已知点出发，自由地向前伸展，既不闭合也不附合到另一已知点的支导线，如图7-7（c）所示。其中，闭合导线本身有严格的几何条件可供检核，常用于建立小测区的首级平面控制；附合导线也具有检核条件，常用于加密平面控制点。支导线没有检核条件，一般不宜采用；在特殊情况下需要采用时，最多只能支出两点。

图7-7　经纬仪导线布设形式

采用何种导线布设方案是根据测区原有控制点的分布情况确定的；一般应先在原有地形图或控制点分布图上进行设计，再到实地踏勘选点。点位选择应考虑下述要求：

（1）点位视野开阔，土质坚实，便于安置仪器测绘地形。

（2）相邻点间地势比较平缓，没有障碍，便于测距和测角。

（3）相邻两导线边长应大致相等，以免测角时因望远镜调焦幅度过大引起测角误差。

（4）导线总长应不超过0.8M m（M为测图比例尺分母）；边长最短不应短于50m，最长不应超过300m。

点位选好后，打下木桩或埋设混凝土柱石，桩柱顶面刻划一个“+”字标记，并按前进顺序编写点号（闭合导线应按逆时针方向编号）。

2.边长测量和角度观测

导线边长可用第六章第三节所述任何一种方法测定。由于测边方法不同，分为红外测距导线、钢尺量距导线和视距导线。作为图根控制，通常可用钢尺量距导线；按照钢尺量距的一般方法，往、返各量一次，相对较差应不大于1/2000。视距导线的精度太低，只能在某些情况下用来加密测站点，将在本章后面讲述。

经纬仪导线的转折角观测，一般应从导线起点开始，逐站观测导线前进方向左侧的角度（左角）。对于图根导线，其转折角采用DJ6型经纬仪按测回法观测一个测回，上、下半侧回之间变动度盘90°，两个半测回角值之差应不大于36″。当导线边与高级控制边连接时，应在连接点上观测连接角，如图7-7（b）所示中∠AB2和∠4CD；不与高级控制边连接的独立闭合导线，应用罗盘仪测定起始边的磁方位角。

经纬仪导线观测手簿如表7-4所示。表中所记是闭合导线（见图7-8）的部分数据。

（二）导线点的坐标计算

导线测量外业工作完成之后，应仔细检查观测手簿，有关数据应当齐全、正确，观测误差应在允许范围之内。计算坐标之前，应先画好导线方位略图，标明点号，弄清起讫点和连接边的关系。计算时必须采用表格（见表7-5和表7-6），先按顺序填好点号，再将有关数据填写在相应的栏目中，互相对应，以免发生错误。

表7-4　经纬仪导线观测手薄

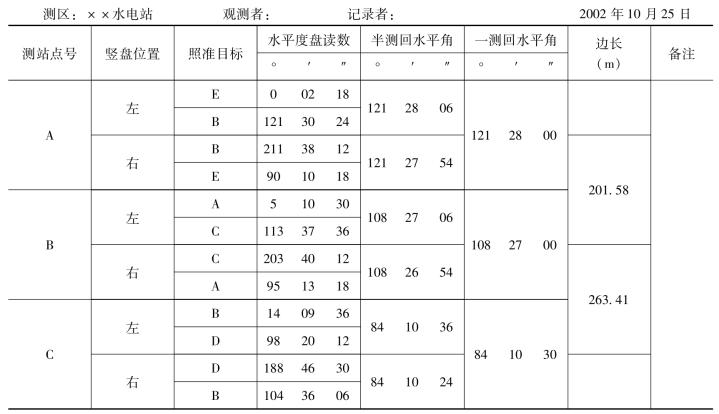
1.闭合导线的计算

（1）角度闭合差的计算和调整。根据几何定理，多边形闭合导线各内角之和应等于（n-2）180°。由于测角存在误差，所测各内角之和∑β测将不完全满足这一条件，于是产生角度闭合差

对于图根导线（量距导线），fβ应不超过下述规定

式中　n——测角个数。

当角度闭合差在允许范围内时，可按反号平均分配法则配赋给各观测角，求得改正后的角度

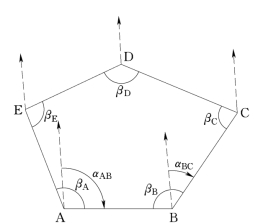
图7-8　闭合导线方位角的推算

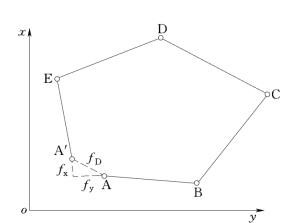
图7-9　闭合导线坐标增量闭合差

按（-fβ/n）式计算的改正数，取位至秒，填入表7-5中第2栏观测角秒值的上方。改正后的角值填入第3栏，其总和应等于（n-2）180°；如果改正数（-fβ/n）不是整数，由于取舍原因，可能使最后结果不完全满足（n-2）180°这一条件，相差1″～2″，应使边长最短的夹角多（或少）改正1″。

（2）导线边方位角的推算。在一般情况下，导线边的方位角是根据左角公式（6-46）来推算的。如图7-9所示；由起算边的方位角αAB推算出去，经过A点上的观测角βA又推算回来，算得的起始边方位角αAB应等于原来的数值，如果不等则说明计算有误。

（3）坐标增量计算及其闭合差的调整。坐标增量按第六章第三节所述式（6-48）用电子计算器进行计算，可使用计算器上的坐标计算专用程序键。算出的坐标增量Δx填入表7-5第6栏，Δy填入第8栏。增量前面一定要写上符号：正的要写上“+”号，负的写上“-”号。坐标增量的取位应和边长取位一致。

由于闭合导线的起点和终点同为一点，显然，纵坐标增量Δx的代数和以及横坐标增量Δy的代数和都应当等于零。但因边长和角度观测存在误差，其中角度虽经调整满足了多边形内角和的几何条件，却并未使边角的对应关系完全符合，由此所算坐标增量的代数和将不等于零，而含有一个差数，称为坐标增量闭合差，分别以fx和fy表示，即

由于存在增量闭合差fx和fy，导线不能形成闭合多边形，如图7-9所示。图中fD称为导线全长闭合差，可按下式计算

对于图根导线，fD应≤0.0004M（m）（M为测图比例尺分母）。

当fD满足规定时，须将增量闭合差以相反的符号按与边长成比例的法则配赋给各个增量，即任一增量Δxi和Δyi应得的改正数为

式中　Di——相应边长；

　　　∑D——导线全长。

增量改正数注于计算表中相应的坐标增量上方。

（4）导线点的坐标计算。在导线上，所求点的坐标等于相邻点的已知坐标与其间的坐标增量及增量改正数的代数和。按照这一法则，从起点开始逐点往下推算，经过一环之后又算得一个起点坐标，与原来的坐标应当相等，以此检核计算是否有误。

闭合导线本身虽有严格的几何条件，可以检查和发现观测及计算中的错误，但如果用错了起算方位角，弄得与实地方位完全不符却不能及时发觉，以致到测图时才可能知道。这是闭合导线的缺点。在计算时应当特别注意，不能用错起算方位角和抄错起算点的已知坐标。

闭合导线的计算如表7-5所示，表中M=1000。

表7-5　闭合导线的计算（用计算器）

2.附合导线的计算

图7-10为附合导线，AB和CD为导线两端的连接边，其方位角αAB、αCD以及起讫点坐标xB、yB和xC、yC均为已知。

图7-10　附合导线计算略图

附合导线的计算步骤及其所用表格与闭合导线相同；但因几何条件不同，角度闭合差及增量闭合差的计算有些区别。

（1）角度闭合差的计算。由于附合导线两端的方位角均为已知，从起算边的方位角αAB经过各转折角推算至终了边，所算得的终了边方位角α′CD应和已知的αCD相等，若不等则有闭合差fβ

为了求得α′CD，通过逐边进行推算，可以导得一般公式。由图7-10，根据方位角推算法则可得

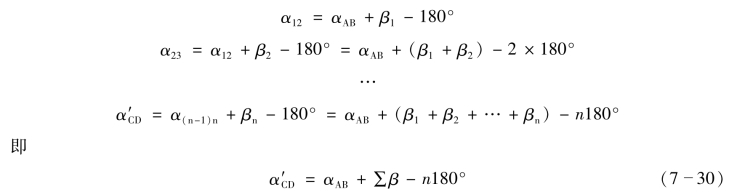
式中　n——参加推算方位角的观测角个数。

根据式（7-30）算得α′CD后，代入式（7-29）计算闭合差fβ。fβ的允许值以及调整方法与闭合导线完全相同。

（2）增量闭合差的计算。附合导线坐标增量的代数和，应等于终点C和起点B两个已知坐标之差；如果不等，则其差数即为增量闭合差，因此，计算公式为

求得增量闭合差后，按式（7-27）计算导线全长闭合差fD。fD的允许值以及增量闭合差的调整与闭合导线完全相同。

附合导线的算例如表7-6所示，表中M=1000。

三、经纬仪交会法测量

（一）经纬仪交会法的布设形式

经纬仪交会法是加密图根点常用的方法，它有三种基本形式：

（1）前方交会。在两个已知控制点上，分别对待定点观测水平角以计算待定点的坐标，如图7-11（a）所示。为了进行检核和提高点位精度，在实际工作中，通常须在3个已知控制点上进行交会，由两个三角形分别计算待定点的坐标，取两组坐标的平均值为所求结果，如图7-11（b）所示。

（2）侧方交会。在由两个已知控制点A、B和待定点P所组成的三角形中，分别在已知点A和待定点P观测水平角以计算待定点P的坐标，如图7-12（a）所示。为了进行检核，一般还在P点对另一已知控制点观测一个检查角ε，如图7-12（b）所示。

表7-6　附合导线计算（用计算器）

图7-11　前方交会

图7-12　侧方交会

（3）后方交会。在待定点上对3个已知控制点观测3个方向间的水平角以计算待定点的坐标，如图7-13（a）所示。为了进行检核，一般还应对第4个已知控制点观测一个检查角ε，如图7-13（b）所示。

为了提高交会点的解算精度，待定点上的交会角应大于30°和小于120°；水平角采用DJ6型光学经纬仪按方向观测法观测两个测回。

（二）交会点的坐标计算

1.前方交会的计算

如图7-14所示，设A、B为已知控制点，P为待定点；A、B、P三点按逆时针顺序排列。A、B点的坐标分别为xA、yA和xB、yB；根据A、B两点上的观测角α和β计算P点的坐标xP、yP，其公式推导如下：

图7-13　后方交会

图7-14　前方交会的计算原理

由图7-14可知

将式[7-32（b）]代入式[7-32（a）]，得

将上式两端同乘以sinα，得

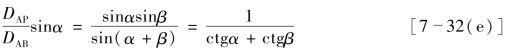
将式[7-32（e）]代入式[7-32（d）]，经整理后得

式（7-32）即著名的戎格公式，又称余切公式。

为了确保计算无误，应根据两个不同的三角形分别计算P点的坐标，如表7-7的算例所示。根据两组坐标计算点位较差f

当f≤0.0002M（m）（M为测图比例尺分母）时，取两组坐标的平均值作为所求结果。

表7-7　前方交会点计算

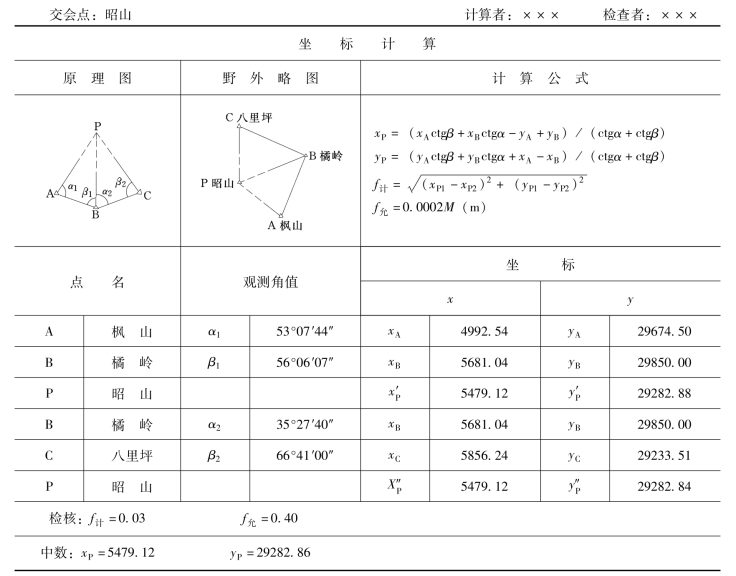
注 本例M=2000。

2.侧方交会的计算

如图7-12（b）所示，侧方交会点P的坐标可根据三角形ABP用戎格公式进行解算。为此，先应算出控制点B上的β角；显然，β=180°-（α+γ）。

为了检查侧方交会点位的可靠性，应根据算得的P点坐标和B、K两点的已知坐标反算出方位角αPB、αPK以及距离DPK。若观测和计算结果没有误差，则αPB-αPK=ε；若有误差，则令

如果Δε≤±即（秒）时，成果即符合要求。

侧方交会点的计算如表7-8所示。

表7-8　侧方交会点计算

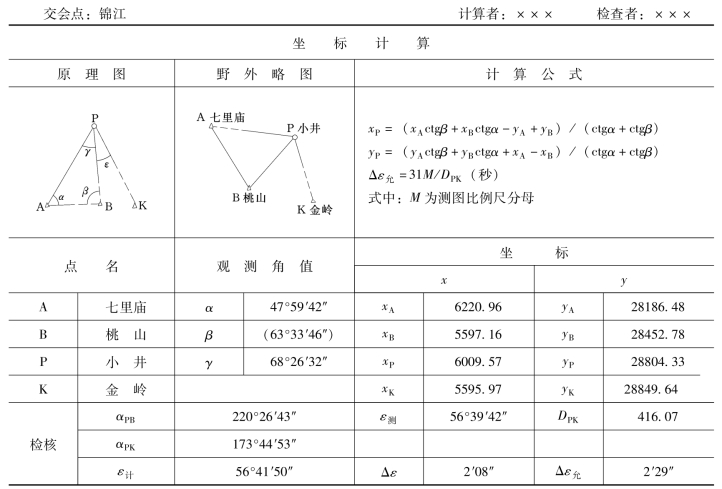
注 本例M=2000。

3.后方交会的计算

后方交会的计算方法很多，下面介绍安谢麦特解法（即重心公式）。

如图7-15所示，设已知点A、B、C组成三角形，其内角分别以∠A、∠B、∠C表示。在待定点P上有3个观测角：α对应BC边，β对应AC边，γ对应AB边，即它们分别与∠A、∠B、∠C所对应的边相同。另外还观测了一个检查角ε。现给出P点的计算公式如下

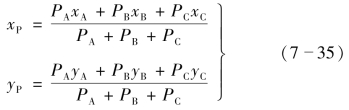
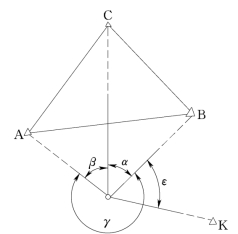
图7-15　后方交会的安谢麦特解法

式中　PA=1/（ctgA-ctgα）；

　　　PB=1/（ctgB-ctgβ）；

　　　PC=1/（ctgC-ctgγ）。

上述公式简明易记，若∠A、∠B、∠C有现成数据，解算P点坐标十分方便；若无现成数据，须根据A、B、C点的坐标通过反算求得。在解算出P点坐标后，应像侧方交会那样进行检核，其Δε亦应≤31M/DPK（秒）。

在式（7-35）中，若α=∠A，β=∠B，γ=∠C+180°，则PA、PB、PC无解，亦即Px、Py无解。因为此时P点位于ΔABC的外接圆上，在此圆上的任何一点都有相同的观测角值，而对应的坐标却不相等；该圆称为后方交会的危险圆。在野外选择后方交会点时，应使之远离危险圆。

后方交会的算例如表7-9所示。

表7-9　后方交会点计算

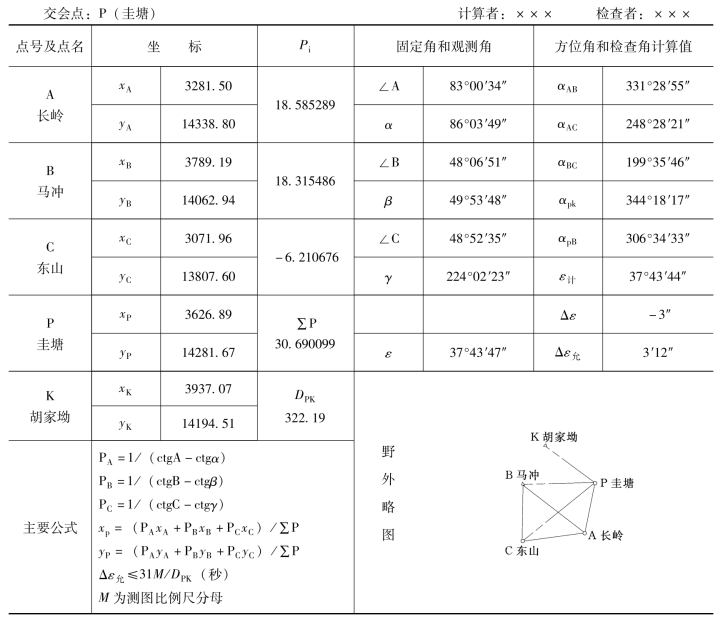
注 本例M=2000。

四、小三角测量

在小区域内进行的不属于国家基本控制等级的三角测量称为小三角测量。它的特点是边长短，计算时不考虑地球曲率影响，观测结果按近似平差方法处理。小三角测量可以作为小测区的首级平面控制，作为加密图根点的基础。

（一）小三角测量的外业工作

1.布点形式和点位选择

小三角测量的布点形式主要有单三角锁、中点多边形和介于两已知控制点间的线形锁，如图7-16所示。三角锁或线形锁适用于较狭长测区；中点多边形适用于较开阔的方圆测区。

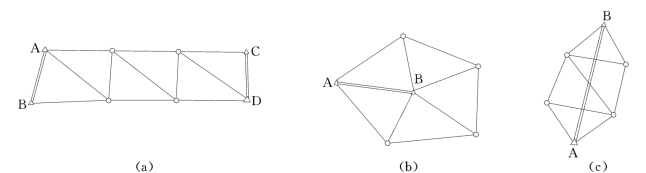
图7-16　小三角测量的主要布点形式

无论采用何种布点形式，选择三角点时都应注意下述要求：

（1）点位应通视良好，土质坚实，便于安置仪器。

（2）三角形各内角应大于30°和小于120°，各边长度应在100～1000m。

（3）基线位置要地势平坦，没有障碍，便于测定距离。

（4）两基线间三角形数目应不超过12个。

点位选好后，打下大木桩或埋设混凝土标志，编定点号，并树立觇标（见图7-16）。

2.基线丈量和角度观测

独立三角锁或中点多边形，其基线长度可用第六章第三节所述钢尺丈量的精密方法进行测定，往、返丈量结果的相对较差应小于1/7500。在丈量基线长度的同时，还须用罗盘仪测定基线边的磁方位角，以作为推算各边坐标方位角的起算数据。

三角点上的水平角观测采用方向观测法，用DJ6型光学经纬仪观测两个测回，或用DJ2型经纬仪观测一个测回。三角形闭合差不应超过60″；用菲列罗公式计算的测角中误差不应超过±20″。

（二）小三角测量的计算

小三角测量采用近似平差，即去掉某种复杂的几何条件，将部分几何条件所产生的闭合差分别进行调整，使平差后各观测值之间的矛盾得到较为合理的解决。然后用经过近似平差的观测值（称为平差值）去推算各点的坐标。

图7-17　单三角锁计算略图

1.单三角锁的计算

在计算之前，应先绘制略图，从起算边开始，将各三角形按顺序编号，如图7-17所示。起始边长以D0表示；由起始边向前推算边长所经过的边称为传距边，以Di表示（i为相应三角形的编号）。传距边所对的角称为传距角；因为一个三角形中的传距边在本三角形是待定边而在下一个三角形中则是已知边，作待定边时所对的角以ai表示，作已知边时所对的角以bi表示。另一角称为间隔角，以ci表示，它所对的边称为间隔边，是三角锁（网）的外围边。

在独立测区，单三角锁两端一般都丈量了基线，因而有两组几何条件：一组是图形条件，即三角形各内角之和应等于180°；另一组是基线条件，即由起始基线通过各传距角推算出的终边基线长度应等于实际丈量的长度。近似平差时，对这两组几何条件所产生的闭合差分别进行调整。

（1）三角形闭合差的调整。各三角形的内角和应等于180°，否则，其差值即为闭合差，以表示有

根据反号平均分配法则将fi配赋给相应三角形的三个内角，即每角分得第一次改正数(www.xing528.com)

于是第一次改正后的角度为

角度平差结果取位至秒。平均配赋闭合差时，若剩1″则大角多配1″，少1″时则大角少配1″。

（2）边长闭合差的调整。以第一次改正后的传距角和起始基线长度D0推算各求距边的长度

式中　′——三角锁终边基线的推算长度。

将取成自然对数

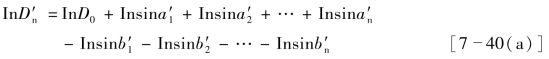
虽是经过第一次改正后的角度，但仍然存在误差，以致亦产生相应的误差。这些误差很小，分别以它们的微分dai、dbi和dDn表示。根据微分法则，取式[7-40（a）]的微分

由于各角的观测条件和技术要求相同，属于等精度观测，故认为各角的观测误差也相等，即

因此，式[7-40（b）]变为

式中，误差dDn即终边基线的推算长度与丈量结果（已知长度）之差，称为基线条件闭合差；对一般小型图根锁而言，应不大于1/1000。

为了消除闭合差dDn，必须在传距角中分别加上一个改正数和即将它们的观测值进行第二次改正。为了求得改正数和根据改正数的大小和误差的大小相等而符号相反的法则，可将式[7-40（c）]中的da和db分别以和代替，于是式[7-40（c）]变成

为了不破坏第一次改正后已经满足的图形条件，必须强使改正数与的代数和等于零，即使或使-根据这一条件，由式[7-40（d）]可解得观测角的第二次改正数

式中　dDn=-Dn；

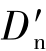　　　′——按式（7-39）推算的终边基线长度；

　　　——已知的终边基线长度。

三角形各内角第二次改正后的角值（即平差值）为

根据平差后的角值再去推算各三角形的边长；由起始基线边推算至终端基线边，其闭合差应等于零。

三角锁近似平差算例如表7-10所示。

（3）坐标计算。一般独立三角锁只一个端点具有已知坐标或假设坐标，为了求得各三角点的坐标，须沿三角锁的外周边按逆时针方向组成一条闭合导线进行推算，算得的坐标增量之代数和应等于零，以此检核计算是否有误。如果起端两点都有已知坐标，亦可根据戎格公式逐点进行推算；此时，为了避免错误，须推算两次，其结果应完全一致。

2.中点多边形的计算

计算之前，亦应先绘制略图，将各三角形和观测角依次编号，编号规则与单三角锁相同，其间隔角ci自然都在中心点上。

中点多边形（见图7-18）只有一条基线，但有3个几何条件，即图形条件、圆周角条件和边长条件。近似平差时，将图形条件和圆周角条件两者的闭合差合并调整，求得观测角的第一次平差值；然后用第一次平差值计算边长闭合差，并在不破坏第一次平差条件的前提下进行调整，求得观测值的最后平差结果。

图7-18　中点多边形计算略图

（1）三角形和圆周角闭合差的调整。设各三角形闭合差为fi，首先将它反号平均配赋给相应三角形的各角，于是中点角ci各得-fi/3的图形条件改正数，所有中点角之和∑ci共增加-∑fi/3。因为采用全圆方向法观测时，∑ci原已等于360°，故所增加的-∑fi/3即为圆周角闭合差，于是各个ci角应分得圆周角条件改正数为+∑fi/3n（n为三角形个数，亦即中点角的个数）。为了不破坏已经满足的图形条件，ai、bi必须作相应的改正，其改正数应为-∑fi/6n。令

各角先后所得图形条件及圆周角条件改正数之和即第一次改正数，分别以和表示，则

将上述改正数加到相应的观测角中，即得到第一次平差角值及由于K值一般较小，计算时应取至0.1″，而配赋到角度上时应先将2K凑整到秒。凑整后的2K为奇数时，K则不为整数，可将ai、bi中较小角度所配K值舍去尾数，让较大角度所配K值收尾凑整。若2K凑整时一次舍入较大，惟恐∑c′i不等于360°，可依三角形次序一舍一入，如表7-11中的算例所示。

（2）边长闭合差的调整。以传距角的第一次平差值和起始边（基线）长Do推算各传距边长，最后推回到起始边，得

由于有误差，以致不等于D0，而产生相应的误差dD0；仿照单三角锁推导第二次角度改正数的方法，可得

而dD0事实上很小，即，故式[7-45（b）]可变成

将式[7-45（c）]代入式[7-45（a）]，得

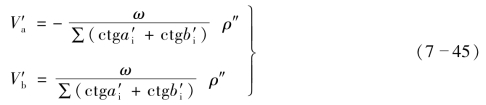
式中，ω一般称为极条件闭合差，按下式计算

ω应不大于0.001。

将第二次改正数加到第一次改正后的传距角值中，即得传距角平差值未进行第二次改正，故平差值等于

根据平差后的角值再推算各三角形的边长，其闭合差应等于零。最后按闭合导线推算各点的坐标，坐标增量闭合差亦应当等于零。

中点多边形的近似平差算例如表7-11所示。

3.无定向线形锁的计算

图7-19　无定向线形锁解算原理

两端附合在两个高级控制点上而没有基线的三角锁称为线形锁；其中，起始方位角也没有（即未测连接角）的线形锁称为无定向线形锁。在高级控制点稀少、通视条件较差的情况下，常用这种线形锁发展图根点。

图7-19所示为布设在两高级控制点A、B之间的无定向线形锁，除已知A、B两点的坐标外，没有其他起算数据，不能直接推算边长和方位角。在解算这种三角锁时，通常先给起算点A的右邻点（图7-19中的2点）假定一个坐标，再根据A点坐标和右邻点的假设坐标以及有关观测角，用戎格公式推算其余各点（包括B点）的假设坐标。由算得的假设坐标反算出假设边长及假设方位角，与实际边长DAB及实际方位角αAB比较，求得缩放系数K（即DAB∶）和方向偏差δa（即αAB-），然后对假设坐标进行缩放和旋转改正，求得各点的实际坐标。具体解算步骤如下：

（1）从起算点A开始，将三角形各内角用a、b、c按逆时针排列表示，使其将要推算假设坐标的一点上为c角；然后配赋三角形闭合差，求得改正后的角度。

（2）根据A点坐标及其右邻点的假设坐标（最好使之接近实际情况）和改正后角度，用戎格公式推算各点的假设坐标

（3）计算辅助系数θ1、θ2及K1、K2有

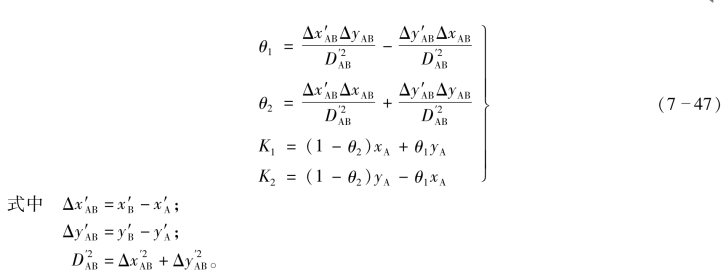
（4）计算各点的坐标为

无定向线形锁的算例如表7-12所示。

表7-12　无定向线形锁计算（用计算器）

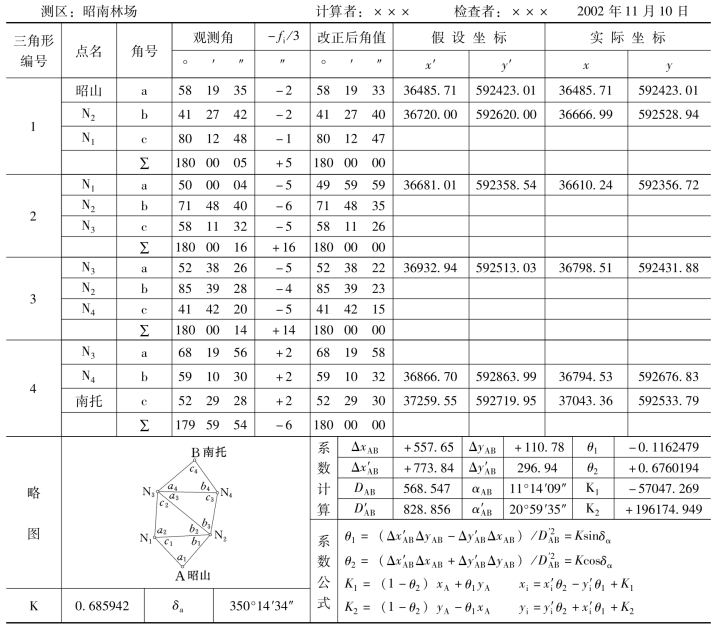
由于无定向线形锁没有检核条件，如果用错起算数据或弄错了观测数据与点号的关系，通过旋转缩放的计算亦能强制附合，不能反映错误情况。因此，必须特别注意检查起算数据和观测数据的抄录是否正确，它们在表中的位置不能填错；解算出的假设坐标和辅助系数应进行复算校核。

假设坐标及真坐标的计算只取至0.01m；但辅助系数K1、K2及假设边长D′AB须取至小数点后第3位，θ1、θ2须取至小数点后第7位。

五、三、四等水准和五等水准测量

在水利水电工程测量中，常用三、四等水准测量建立较高精度的高程控制网，用五等水准（又称图根水准）测量从高一级的水准点引测图根点的高程。五等水准测量所用仪器工具、操作程序、记录表格和计算方法都和三、四等水准测量比较接近，主要只是限差要求不同。现将这3个不同等级水准测量的具体要求列于表7-13中。

表7-13　三、四、五等水准测量技术要求对照表

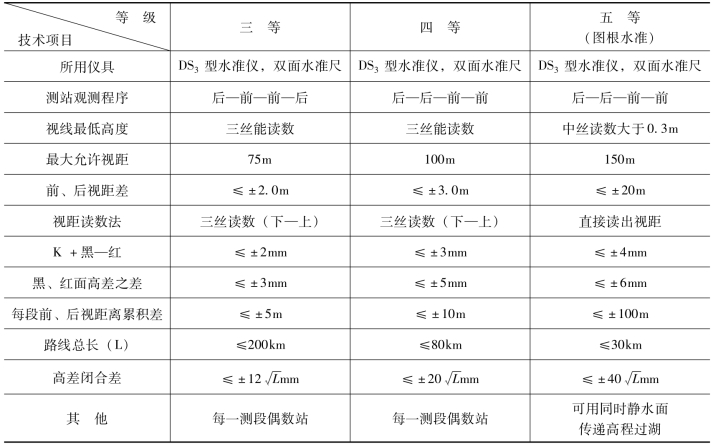
由于四等水准测量应用更为广泛，而且通过学习和掌握四等水准测量，对三等和五等水准测量也就可以掌握了，因此，下面重点介绍四等水准测量。

（一）水准路线的选择和水准点的设置

四等水准路线一般是根据工程建设或地形测量的需要而布设的，究竟采用附合路线还是闭合路线，须视已知高级水准点的分布情况而定；路线总长应不超过80 km。为了便于施测和尽量减少测量误差，所选路线应当坡度比较平缓，避免通过土质松软和存在滑坡、塌方等不良地质现象的地段。在路线上每隔一定距离或所需位置上埋设一个水准点。凡需长期保存的永久性水准点，应采用图7-5所示的混凝土柱石，埋入地下，掩上护盖。只需短期保存的水准点，可在固定建筑物（如屋基、桥墩等）或裸露的岩石上凿刻标记，亦可打入大木桩，在桩顶钉一颗圆头钉表示。为了便于日后寻找（特别是埋入土中的永久性水准点），一般每个点都应绘制点位略图，在图上标明水准点与周围固定地物的相对方位和距离。这种略图称为水准点之记。水准点的编号方法如第六章第一节所述。

（二）观测程序和记录方法

四等水准测量一般采用DS3型水准仪和双面水准尺进行观测。为了抵消因磨损而造成的标尺零点差，每段（即两相邻水准点之间）的测站数目应为偶数。各段记录应分开。在每一测站上，先安置水准仪，概略整平后分别瞄准前、后水准尺，估读视距；最大视距不应超过100m，前后视距之差应不超过3m。否则，应当移动前视水准尺或水准仪，以满足要求。然后按照下述步骤进行观测和记录（见表7-14）：

（1）照准后视尺黑面，使水准管气泡居中，按下丝（1）、上丝（2）、中丝（3）的顺序读数记录。

（2）照准后视尺红面，读取中丝读数，记录于（4）。

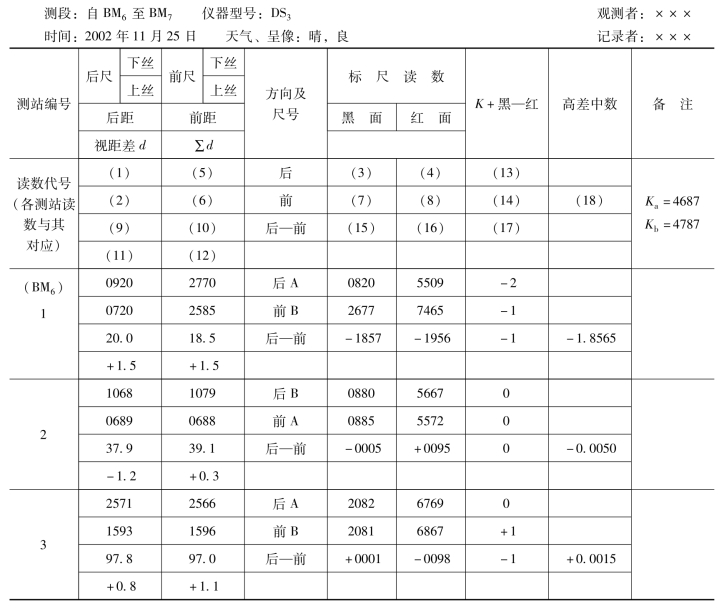
表7-14　四等水准观测记录

续表

（3）照准前视尺黑面，使水准管气泡居中，按下丝（5）、上丝（6）、中丝（7）的顺序读数记录。

（4）照准前视尺红面，读取中丝读数，记录于（8）。

这样的观测顺序简称为后—后—前—前。观测完后应立即进行计算和校核，符合要求方可迁站，不符合要求则须重新观测。

（三）测站计算与校核

一般观测和记录都以毫米（mm）为单位，黑面和红面高差计算亦以毫米为单位。但前、后视距和高差中数应以米（m）为单位；其中高差中数取至小数点后第4位（即取至0.0001m），若第4位无数应添“0”表示。计算顺序如表7-14中圆括号编号所示，具体要求如下：

（1）前、后视距之差d（后距减前距）不应超过±3m，记于（11）。

（2）前、后视距累积差∑d（即本站前、后视距差与上一站的前、后视距差的代数和）记于（12）；每一段的前、后视距累积差不应超过±10m。

（3）前、后视的“K+黑-红”都不应超过±3mm。

（4）黑面高差与红面高差（加或减100mm后）之差应不超过±5mm；红面高差加（或减）100mm后，与黑面高差平均，记于（18）。

由于两支水准尺的红面读数相差100mm（即4787与4687之差），因此红面测得的高差应加（或减）100mm才等于实际高差；到底是加还是减可以黑面高差为准来确定。当前、后两点间的高差小于100mm时，红面高差与黑面高差符号相反，像表7-14中第2站及第3站即如此。这时，如果黑正红负，必定是B尺（4787）为前视，则红面高差应加100mm；若黑负红正，必定是A尺（4687）为前视，则红面高差应减去100mm。

（四）成果整理和高程计算

1.各段长度及高差的计算与校核

（1）视距部分。这部分的计算与校核可按下述程序和方法进行：

1）分别算出后距总长和前距总长。

2）计算前、后视距累积差：∑d=后距总长-前距总长，应与记录中对应各段最后一站的∑d相等。

3）求取测段总长：Li=后距总长+前距总长。

（2）高差部分。这部分的计算和校核必须按下述程序和方法进行：

1）分别计算黑面总高差和红面总高差：∑h黑=∑a黑-∑b黑；∑h红=∑a红-∑b红。

2）计算全段高差：高差中数总和∑h=（∑h黑+∑h红）/2。

应当注意：此处规定采用偶数站观测，故红面总高差中不存在加或减100mm的问题。如果是奇数站，并且是A尺（4687）为首站后视，B尺（4787）为末站前视时，则红面总高差中应加上100mm；当B尺为首站后视，A尺为末站前视时，红面总高差中应减去100mm。

2.高差闭合差的调整和高程计算

四等水准路线的高差闭合差应不超过±20（L为路线总长，以km计）。符合此要求时，须将闭合差反号，按与测段长度成比例的分配法则配赋到各段高差中，然后逐点推算高程（参见第六章第一节）。

六、过河水准测量

当水准路线跨越河流、湖泊、峡谷等地段时，如果这些地段宽度太大，视线长度远远超过相应等级水准测量的有关规定，不但难以精确地读取标尺读数，而且由于前、后视距不等，测得的高差中将包含水准仪的i角误差、地球曲率和大气折光影响。为了解决这一问题，求得比较精确的观测结果，必须采取特别措施。在这种情况下进行的水准测量，统称为过河水准测量。

过河水准测量的步骤和方法如下：

（1）在水准路线附近，选择河面最窄、两岸高差不大，且地质条件和通视情况良好的地段布设测站点A、B（见图7-20）。A、B两点离水边的距离应大致相等，视线离水面高度一般应在2m以上（当河面宽度超过300m时，应在3m以上），且仪器不能靠近墙壁和砖石堆，以保证周围开阔、通风。

（2）在两岸分别选取离A、B各10～20m的两点Ⅰ、Ⅱ作为临时水准点，并使DAⅠ=DBⅡ。

A、B、Ⅰ、Ⅱ的4点均应打下大木桩，桩顶钉一颗圆头钉。

（3）精确测定辅助高差hⅠA和hBⅡ。测量时，仪器至前、后视标尺的距离应尽量相等。为了避免标尺零点差的影响，前后视用同一标尺进行观测。

（4）在A点安置水准议，以近点Ⅰ为后视，远点B为前视，测定高差hⅠB（B点应读数3次取平均值）；然后，在保持望远镜调焦螺旋不动的条件下，将水准仪安置于B点，以远点A为后视，近点Ⅱ为前视，测定高差hAⅡ（A点应读数3次取平均值）。完成hⅠB及hAⅡ的一次观测称为一个测回。

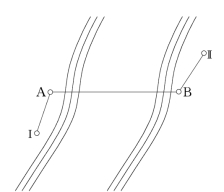
图7-20　过河水准测量的布点方法

（5）按下式计算Ⅰ、Ⅱ两点间的一测回高差

不难证明，按此法测算的高差hⅠⅡ中将不包含水准仪的i角误差及地球曲率和折光差的影响。

过河水准至少需要观测一个测回。当河宽超过200m时，应增加测回数，在上午和下午各观测1～2个侧回。观测第二测回时，两岸的标尺应互相对调，以抵消两尺零点差的影响。四等水准的高差测回差应小于16mm；三等水准应小于8mm。将各测回高差取平均值为最后结果。

过河水准测量记录如表7-15所示。括弧内的近点红面读数只起校核作用，不用于计算高差；因此，“K+黑-红”最好等于零。

表7-15　过河水准测量记录

注 HⅠⅡ=（hⅠA+hBⅡ+hⅠB+hAⅡ）/2=+0.450。

因距离太远，隔河往往看不清读数，此时可采用硬纸或硬塑料片制备一块简易觇牌，如图7-21所示。观测时，在立尺点上由专人手持觇牌，依照观测者的旗语指挥，沿水准尺上下移动，至觇牌上的红白界线落到望远镜中丝上时，由持牌者读取觇牌上尼龙丝所指的水准尺读数。三次读数的较差最大不应超过15mm。

七、三角高程测量

在第六章第三节中，高差公式：h=D/tg Z+i-v，这里D是通过视距测量测定的地面两点间的平距。在交会法和小三角测量中，两点间的平距可以通过解算三角形或进行坐标反算求得，如果测定了天顶距，量取了仪器高和觇标高，即可利用这一公式计算高差。按这种方法测定高差去推算高程，称为三角高程测量。当两点间的距离较大时，计算高差须加球气差改正。

图7-21　简易读数觇牌

图7-22　球气差对三角高程测量的影响

（一）考虑球气差影响时的高差公式

如图7-22所示，设在A点安置经纬仪观测B点，欲求高差hAB。A′E为通过竖盘中心的水平面，则EF即为地球曲率对高差的影响（球差）；此外，由于大气折光影响，望远镜照准觇标顶点M时，视线不是直线而是弧线，望远镜的视准轴则沿弧线的切线方向指着M′，实际上等于观测M′的天顶距，故使所算高差中包含了差数MM′，此即大气折光对高差的影响（气差）。球差和气差对高差的联合影响称为球气差，以f表示。由图7-22可知

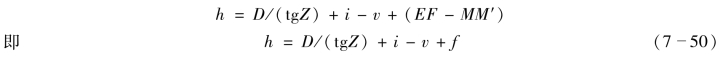
球差的影响很简单，可用公式：EF=D2/（2R）来计算。但气差的影响比较复杂，它与气温、气压及视线倾斜度或地面坡度等因素有关；过去的研究认为：在我国镜内，气差（MM′）的平均值约等于0.11D2/（2R）。

因此，球气差一般采用下式计算，即

为了计算简便，可将式（7-51）简化为f=0.07D2cm（D以百米为单位）。

（二）直觇和反觇的高程公式

在已知高程点A安置仪器，观测待定点B以计算其高程HB，称为直觇。其公式为

在待定点B安置仪器，观测已知高程点A，以计算待定点B的高程HB，称为反觇，其公式为

在一条边上只进行直觇或反觇，称为单觇或单向观测；单觇无检核条件，在高程控制测量中，不能只由一个已知点按单觇去测定待定点的高程。在同一条边上，既进行直觇又进行反觇，称为复觇或对向观测。对向观测可以抵消球气差的影响，从理论上说可以不进行球气差改正；但是，为了将直觇和反觇结果进行比较，衡量较差是否合乎要求，仍须计算球气差。此外，对向观测还可以抵消竖盘偏心差对高差的影响，所以，在一般情况下应采用对向观测，以保证成果质量。

（三）三角高程测量的实施

1.独立交会高程测量

按三角高程测量方法由3个已知点用单觇、或由一条边用单觇而另一条边用复觇测定待定点的高程，称为独立交会高程测量。采用经纬仪交会法测定图根点的平面位置时，常用此法测定其高程，但参与推算高程的边长应不超过0.3M（m）（M为测图比例尺分母）。如果由3个方向单觇计算的高程较差不超过测图基本等高距的1/7时，则取平均值作为最后结果。

独立交会高程测量的计算如表7-16所示。

表7-16　独立交会点高程计算

2.三角高程路线测量

将各三角点依次连成一条高程测算路线，在每一条边上都按三角高程测量进行复觇测定高差，从而推算各点的高程，称为三角高程路线（或多角高程导线）测量。在小三角测量中，如果只有一个已知高程的三角点作为起算点，则以三角锁（网）的外围各边组成闭合路线；如果锁（网）两端各有一个已知高程的三角点，则可组成一条或两条附合路线（见图7-23）。每条三角高程路线的长度一般不应超过1M（m），边长不应超过0.3M（m）。

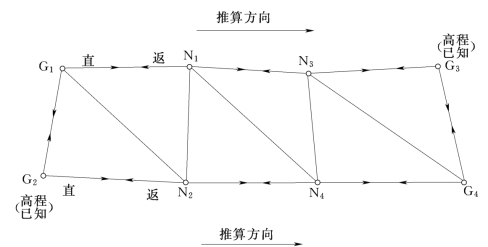
图7-23　三角高程路线

三角高程路线各边直、反觇高差不符值每百米不应超3cm；边长在200m以内时，不应超9cm。高差平均值的符号以直觇（起点至终点的方向）为准。全线高差闭合差不应超过基本等高距的2/7，并按相反的符号与边长成比例进行调整配赋。

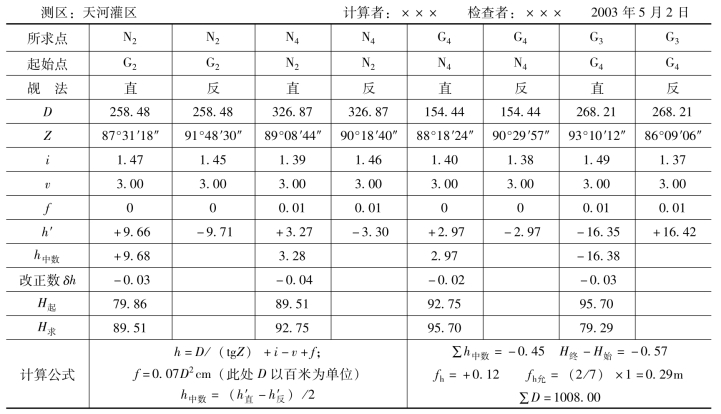
三角高程路线计算如表7-17所示。表中G2为起点，已知高程H起=79.86m；G3为终点，已知高程H终=79.29m。路线上各边高差中数的代数和为-0.45m，不等于终点与起点的高程之差，故有闭合差为+0.12m。将闭合差配赋后再计算高程。

表7-17　三角锁（网）高程路线计算

三角高程测量的精度较低，一般只适用于1∶2000以下的较小比例尺测图时，在山丘区测定图根点的高程。

八、经纬仪视距导线的观测和记录

进行1∶2000以下的较小比例尺测图或查勘性质的测图时，可用视距导线加密测站点。视距导线具有简便灵活的特点，且能同时测定各相邻点间的高差，在水利水电工程测量中经常应用。

经纬仪视距导线应尽量沿着较为平缓的地面布设，以免因坡度太大影响视距精度。导线的最大允许视距为120m（1∶2000测图）和250m（1∶5000及小于1∶5000的测图）；导线全长应不超过0.4M（m）。

（一）一个测站的观测程序和内容

（1）在测站上安置经纬仪，量取仪器高（取至0.01m）。

（2）正镜照准后视标尺，读取视距（下丝和上丝读数，取至0.001m）、截尺（中丝读数，取至0.01m）、竖盘读数和水平度盘读数。

（3）正镜照准前视标尺，读取视距、截尺、竖盘和水平度盘读数。

（4）倒镜照准前视标尺，再照准后视标尺，读数内容与（2）、（3）项相同。但应注意：为了使正、倒镜的截尺相同，以便于计算指标差和天顶距，也为了减少估读误差，提高视距精度，在进行正、倒镜视距时，上丝应照准标尺上同一条整分划线。

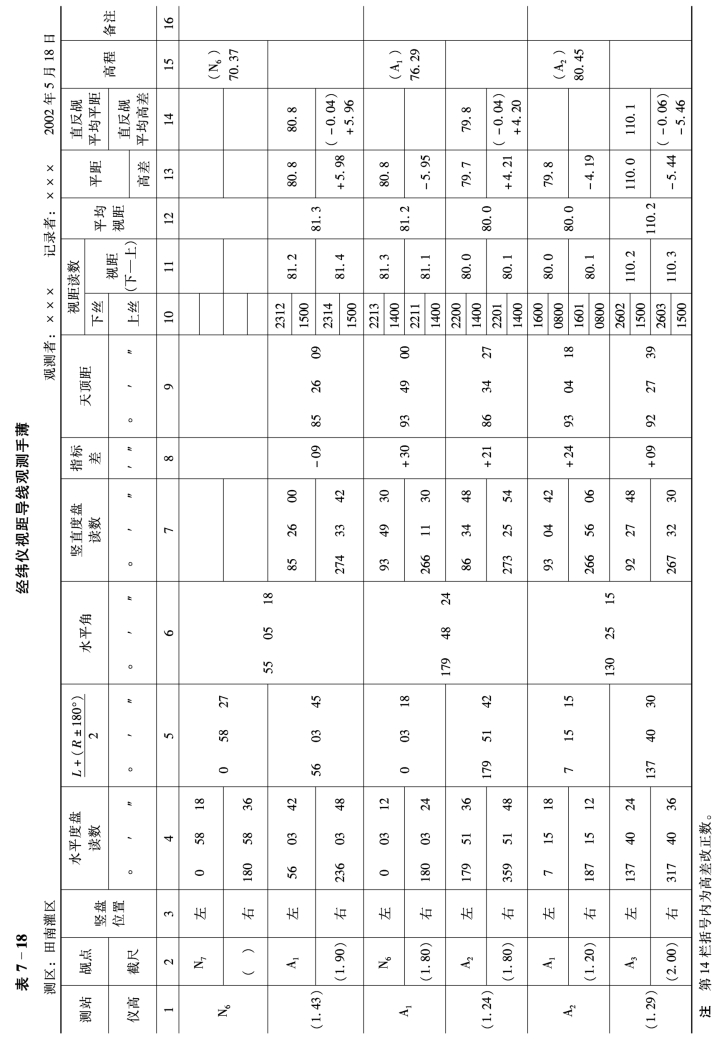
（二）外业手簿的记录、计算和有关要求

视距导线的记录手薄如表7-18所示。其中水平角（按方向观测法）和天顶距的记录计算与第六章第二节所述相同。关于视距、平距、高差和高程的计算应注意以下几点：

（1）正、倒镜视距之差不超过0.2m时才可取平均值，根据平均视距再计算平距和高差。

（2）同一边的直、反觇平距之差应不大于1/200；其平均值取至0.1m，记于相应的直觇栏中。

（3）同一边直、反觇高差的较差δh（按取直、反觇高差的代数和计算）与视线倾斜度α（即|90-Z|）有关，可按δh=Dα（cm）计算（α以度为单位，不足3°时以3°计。D以百米为单位，不足100m时以100m计）。高差平均值取至0.01m，符号一般以直觇为准，并记于直觇栏中。当两点间高差很小时，因观测误差影响可能使直、反觇高差出现相同的符号，此时应按“平均高差=（直觇高差一反觇高差）/2”来决定结果。

（4）高差闭合差应不超过基本等高距的2/7，并以相反的符号按与边长成比例的法则将闭合差配赋到各边的平均高差中，然后计算各点的高程。高程取位至0.01m，记在高程栏中与点号相应的横线上。

视距导线的方位角闭合差fa≤±坐标增量和坐标值的计算均取至0.1m；按式（7-27）算得的导线全长闭合差fD≤0.0008M（m）。