测量距离与直线导向技巧

一、视距测量

水准仪和经纬仪的十字丝分划板都有上、下两条较短的水平丝，可以用来测量距离，称为视距丝（参见图6-4和图6-46）。用视距丝按几何光学和三角学原理测定平距和高差的方法称为视距测量。

（一）视距测量的原理

1.视线水平时的视距公式

图6-66为内对光望远镜视准轴水平时照准视距标尺（或水准尺）的光路图。如果望远镜中不装调焦透镜L2，则标尺上间隔为l的A、B两点经物镜成像于a′、b′，间隔为p′；其成像位置满足焦距为f1的凸透镜光学公式，但没有落在十字丝平面上。这时若在望远镜内装上调焦透镜（凹透镜）L2，则a′、b′经调焦透镜的作用将成像于十字丝平面上的a、b两点，间隔为p。对于调焦透镜来说，a′、b′可看作是a、b的虚像；设物距为x，像距为y，调焦透镜的焦距为f2，根据凹透镜成像的光学公式，则

图6-66　视线水平时的视距原理

因为ΔAF1B∽ΔHF1G，△ao2b∽△a′o2b′，故分别有

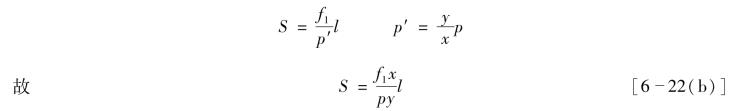
将式[6-22（a）]代入式[6-22（b）]，且注意到图6-66中：D=S+f1+δ，得到

式（6-22）中，x是望远镜照准某个一定距离的目标时，调焦透镜光心o2至十字丝平面的距离。因为目标远近不同，调焦透镜位置随之改变，故x是个变量。设望远镜照准无穷远处的目标时，调焦透镜至十字丝平面的距离为x0，照准其他目标时则为x=x0+Δx，将此关系式代入式（6-22）得

式（6-23）中，K为视距乘常数，C为视距加常数。在仪器制造时，适当选择f1、f2、p等结构参数，可使K=100，C≈0（实际上C不超过2cm），故实用水平视距公式为

即视线水平时，上、下丝在标尺上所截取的间隔（二丝读数之差）乘以100便是仪器至立尺点的平距。

在图6-66中，∠AF1B=φ，为上、下丝对标尺所张的视角，由图可知

即φ=34′22″。

因视线水平，若设仪器高为i，中丝读数（又称截尺）为v，则高差h按下式计算

2.视线倾斜时的视距公式

图6-67为视线倾斜时的视距情况。这时竖直的标尺R不与视准轴OC垂直，上下丝在尺上截取的间隔为AB=l，但不能由l直接按式（6-24）计算平距。为此，设想在C点有一支标尺R′垂直于视准轴OC，上下丝在此尺上截取的间隔为A′B′=l′，则根据l′可按式（6-24）计算斜距OC，从而换算成M、N两点间的平距D。由图6-67可知

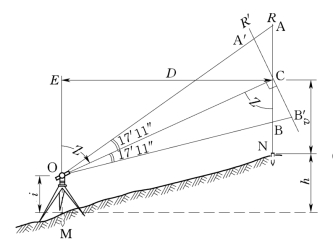
图6-67　视线倾斜时的视距原理

由于实际上并不能读得l′，只能根据假设条件找出l′与l的关系，再根据l来进行计算。为此，首先考察一下△AA′C和△BB′C。由图6-67可知

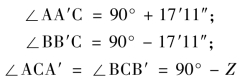
即它们都是十分近似的直角三角形。故有

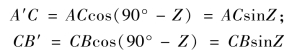
因为l′=A′B′=A′C+CB′，即l′=（AC+CB）sin Z；而AC+CB=AB=l，故

将式[6-26（b）]代入式[6-26（a）]得

此即视线倾斜时计算平距的公式。

由图6-67可知，M、N两点间的高差应为

将上式改成适合于电子计算器运算的形式

当Z=90°时，正切函数没有定义；但D/tg90°=D ctg90°=D×0=0，故高差可直接按h=i-v计算。

如果从视距计算表中查取平距和高差主值时，由于视距计算表是按竖直角编制的，计算公式应改用竖直角α表示。由式（6-14）可知：Z=90°-α；以此代入式（6-26）和式（6-27），经整理得

（二）视距测量的主要误差来源及其消减方法

视距测量所能达到的测距精度与仪器的光学性能以及外界因素的影响有关。在不考虑外界因素影响的条件下，使用一般水准仪或经纬仪所能达到的测距精度为（34v）（v为望远镜放大倍率）。如果受到各种外界因素影响，测距精度将大大降低。一般认为：视距测量的精度最高只能达到1/300。主要误差来源如下：

（1）视距乘常数K和视距标尺分划误差。由于仪器制造工艺上的原因，K值不一定恰好等于100，视距标尺的分划不一定均匀、准确。这时，可以采取量距进行检查测定，配制与所用仪器相适应的专用视距标尺，以减少其误差影响。

（2）用视距丝读数引起的误差。由于上、下丝不是同时读数，眼睛位置变动可能带来视差影响；此外，视距丝有一定的宽度，使估读产生误差。为了减少这些误差的影响，应当精心对光，消除视差，并在观测时尽量不变动眼睛位置；同时应利用望远镜微动螺旋使上丝截取整分米或整米分划，以减少一次估读误差，并便于心算。

（3）外界条件变化引起的误差。如竖向折光影响使视线不成直线（越近地面影响越大）；水气蒸腾时的折光影响使成像晃荡；风力增强使仪器和标尺不稳定；尘雾迷蒙使读数看不清晰，都导致视距测量产生误差。为了减少这些误差影响，应避免在烈日下和尘雾中进行视距测量；观测时应使视线离开地面至少1m。

（4）标尺倾斜误差。标尺扶立不正，前后倾斜是引起距离误差的最主要因素。设标尺倾斜一个ε角（见图6-68）；为说明问题简便起见，令上丝照准标尺零点B，上、下丝截取的标尺间隔为A′B=l′；如果标尺竖直，上、下丝截取的标尺间隔为AB=l。由于l′≠l，故按l′计算的距离就会产生误差。若视距测量时的天顶距为Z，不难证明所测平距的误差为

图6-68　标尺倾斜对视距测量的影响

即标尺倾斜引起平距误差与立尺点对仪器的高差成正比。当视距为100m，天顶距为70°或110°时，平距D=88.3m，立尺点对仪器的高差为32.14m；如果标尺倾斜3°，引起的平距误差为1.68m，相对误差为1/52。这样大的误差是一般测量所不允许的。为了消除或削弱这种误差的影响，标尺必须严格竖直（尺上应有水准器）。当地面高差太大，天顶距小于80°或大于100°时，最好改用水平置尺视距。一般DJ6型经纬仪的十字丝分划板上都有左右两条短纵丝，就是供水平置尺视距用的，其乘常数K亦等于100。按左右丝读取尺上间隔l计算平距的公式如下

高差仍按式（6-27）计算，此时v应为标尺的平置高度。

二、距离丈量

视距测量虽然简便灵活，但测距精度很低。有时为了达到一定精度要求，距离需要用尺丈量。

（一）丈量用尺和辅助工具

距离丈量用尺有20m、30m和50m等几种不同长度的钢尺和皮尺，可以卷放在盒内（见图6-69），分别称为钢卷尺和皮卷尺。钢卷尺由薄钢带制成，一般分划到毫米；也有的只首末两端有一段毫米分划，而中间分划至厘米。钢尺伸缩性小，能用作较精密的丈量，是测量中最常用的丈量工具。皮卷尺由麻纱或化纤与金属丝混织而成，分划只到厘米。皮尺伸缩性大，易受拉力影响，只有在精度要求不高时才能使用。

图6-69　钢卷尺和皮卷尺

由于卷尺长度起算的零点位置不同，有刻线尺和端点尺之分。刻线尺的零点是尺端附近的零分划线，如图6-70（a）所示；钢卷尺大都属于这种类型（但有少数例外，使用时应特别注意）。端点尺的零点在拉环外边缘，如图6-70（b）所示；皮卷尺都属于这种类型。

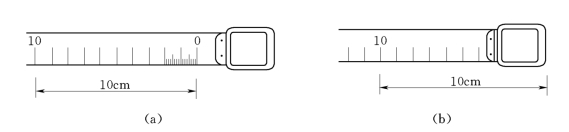
图6-70　刻线尺和端点尺

丈量用的辅助工具主要有花杆和测钎。花杆形式如图6-71（a）所示，用来标定直线；测钎的形式如图6-71（b）所示，用来标记尺端位置和计算已经量过的整尺段数。其他辅助工具还有弹簧秤、垂球、温度计等。

（二）一般丈量方法

1.平地量距

设A、B为平地两点。为了丈量两点间的距离，可先在B点插上花杆（见图6-72）。一人手持钢尺零点，对准起点A作后司尺；另一人手持钢尺另端并带着测钎前进，作为前司尺。后司尺目视终点花杆，指挥前司尺走在AB直线上。当前司尺放完一整尺时，紧靠尺端整尺刻线将测钎插到地上，然后2人持尺同时前进。当后司尺走到所插测钎处时，又像在起点一样指挥操作。如此逐段丈量，一直量到终点B为止，称为往测。每量完一整尺，都应由后司尺收取一根测钎；至终点B时，后司尺所持测钎数目应等于前司尺所插测钎数目n，亦即等于量过的整尺段数。最后一根测钎至B点的距离可能是不足一整尺的尾数，设它为q，则AB的平距为

式中　l——卷尺长度。

图6-71　花杆和测钎

图6-72　平地量距

为了避免错误和提高丈量结果的精度，应由B向A再量一次，称为返测。往、返所量距离之差称为往返较差，以ΔD表示；往返较差与往、返距离平均值之比值，以分子为1的形式表示，称为相对较差。其计算公式为

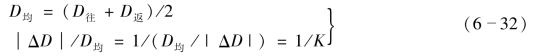
平地量距的相对较差一般应达到1/2000。

2.斜坡量距

在斜坡上丈量距离时，可以采取平拉法，亦可沿坡面量取斜距再进行改正以求得平距。采用平拉法时须由高处向低处分段丈量。如图6-73所示，将钢尺零点对准起点A，当钢尺拉平后，用垂球将尺上某一分划投影到地面上用测钎标定一点并记下此分划读数；再从测钎处往下，仿此一直量到终点B。返测时仍由高处往低处丈量。两次丈量结果的相对较差不应大于1/1000；取平均值作为最后结果。

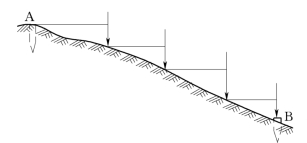
图6-73　平拉法斜坡量距

沿坡面量取斜距时，应分尺段进行倾斜改正求得平距。为此，须测定两尺端的地面坡度或高差。地面坡度可观测地面天顶距代替，观测时应使中丝截取的标尺读数等于仪高。由天顶距将斜距D′化为平距D的公式为

由两尺端高差h将斜距D′化为平距D按勾股弦定理计算

3.钢尺量距应注意事项

（1）弄清钢尺零点和分划注记，不要将刻线尺当成端点尺。

（2）量距时定线要直，拉力要匀，钢尺不能松曲，测钎要插准。

（3）应看清读数和记清整尺段数。

（4）防止钢尺扭结和行人、车辆碾压。

（5）钢尺用完后要擦拭干净，涂上少许机油，卷入盒内。

（三）精密丈量方法

钢尺受温度和拉力变化影响，长度也会发生变化。因此，在一般情况下。钢尺的实际长度并不等于尺上注记的名义长度。为了精确地量得一段距离，首先必须知道在某一温度t0和拉力F0条件下所用钢尺的实际长度与标准衡器长度之差（称为尺长误差），亦即必须进行钢尺检定。在距离丈量过程中，需要同时测定温度和拉力，通常使丈量时的拉力等于检定时的拉力，而尺长误差和温度变化引起的误差则作相应的改正。精密丈量的步骤和方法如下。

1.实地丈量

（1）概量定线。在需要量距的直线一端安置经纬仪，照准另一端，固定照准部，指挥助手清除视线上的地面障碍，沿视线每隔一整尺（约少0.1m）打一木桩，在桩顶用细“+”字中心标出直线点的精确位置。细“+”字的一横应与视线方向大致垂直。

（2）逐段精量。丈量时，钢尺一端用弹簧秤牵引（另一端可以不用弹簧秤），两端尺边紧靠着“+”字中心，使拉力达到规定数值F0（30m钢尺为100N），待稳定后，同时读出钢尺两端“+”字中心所指的读数，并记下当时的温度。然后稍许前后移动钢尺，再进行读数；每段都应连读数3次（温度只需1次），算得3个长度之差应不超过3mm，取其平均值作为该尺段的丈量结果。如此一直量到终点，完成一次往测。再调转钢尺进行一次返测。往返丈量结果的相对较差应小于1/7500。

（3）测定尺段高差用水准测量测定相邻桩顶间的高差，结果取至0.01m。

精密量距手簿如表6-6所示。

表6-6　精密量距手簿

2.距离计算

距离计算时，首先对每尺段进行尺长改正、温度改正和倾斜改正，求得每尺段平距，然后计算出全线距离。计算步骤和方法如下：

（1）计算尺段斜距。将每段尺段的长度li加上温度改正数和尺长改正数，即得每段斜距。计算公式如下：

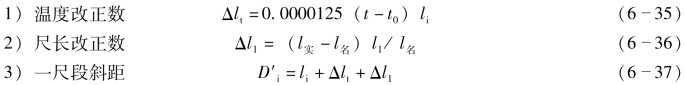
式（6-36）中，l实-l名是在进行钢尺检定时，由标准衡器量得的钢尺实际长度与钢尺上所注记的长度（称为名义长度）之差，亦即该尺的尺长改正数。例如：一支名义长为30m的钢尺，实际只有29.900m，则l实-l名=-0.100m；用这支钢尺去丈量距离，其结果总是偏大，因此改正数应为负值。反之，如果名义长为30m，实际长度却为30.100m，则l实-l名=+0.100m；用这支钢尺去丈量距离，其结果总是偏小，因此改正数应为正值。

（2）计算尺段平距。根据每尺段改正后的斜距D′i和尺段高差hi，按勾股弦定理[见式（6-36）]计算平距Di。

（3）计算全线距离。根据各段平距计算全线距离，即：D=∑Di。

距离计算实例如表6-6所示，表中数据只有往测部分，返测部分省略了。

三、红外测距

红外测距亦称红外光电测距，是以红外光作为测距载波，将测距信号“载于”红外光束上，利用光在大气中的传播速度和传播时间来测定距离。

（一）红外测距原理

光波在大气中的传播速度c是一个已知数值，若能测定它在待测距离上往、返传播的时间t，则可按下式求得距离（见图6-74）

时间t可以直接测定，也可以根据连续的调制波在待测距离上往返传播所产生的相位变化来间接测定。直接测定光波传播时间的测距仪称为脉冲式测距仪，精度很低；根据相位变化间接测定光波传播时间的测距仪称为相位式测距仪，可以达到很高的精度。

由于红外光的产生不需很大的能量，红外发光器还可兼作调制器、因此，配合先进的集成电路可以制造出功耗低、体积小、重量轻、精度高的相位式短程测距仪，即红外测距仪。

红外测距仪的光源是一支砷化镓发光二极管，在管上注入按一定频率f变化的交变电流（测距信号），发出的光强（即振幅和亮度）亦按此频率变化。这种光称为调制光，或称测距信号光，波形为正弦包络线。正弦测距信号某一瞬时状态所对应的角值称为相位；两不同瞬时状态所对应的角值之差称为相位差或相位移。设测距仪在A点向B点发出信号光，被B点的反光镜反回A点并由仪器接收，所经过的时间为t；为说明方便起见。将从B点反回的光波沿测距方向展开，如图6-75所示。由图可以看到测距信号在待测距离上往返一次所经2D路程上的相位变化情况。因为测距信号相位变化的整周期为2π，故它在这段时间内产生的相位移为

图6-74　光的往返传播(www.xing528.com)

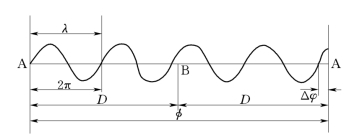
图6-75　测距信号在往、返测程上的相位变化

将式（6-39）代入式（6-38），得

若能测定相位移φ，则根据式（6-40）即可求得距离D，这就是相位法测距的原理。

由图6-75还可看到：φ又可以表示为N个整周期与不足一个整周期的相位尾数Δφ之和，即

将式（6-41）代入式（6-40），得

式中λ=c/f，为调制波长（即测距信号波长）。

若令λ/2=l，则式（6-42）变为

将式（6-43）与钢尺量距式（6-31）比较可以看到：l相当于钢尺长度，故将它称为“光尺”；如果知道测距信号的频率f，则“光尺”的长度即可求得。

相位移是用相位计来测定的；但相位计只能分辨0°～360°的相位值，即只能测定不足一个整周期的相位尾数Δφ或ΔN，不能测定相位变化的整周期数N。因此，当距离大于一个“光尺”的长度时，便不能测得应有的确切结果。为了解决这一矛盾，于是将两个或若干个不同长度的“光尺”配合使用，即在测距仪上至少设置两个调制频率：一个为精测频率，“光尺”较短，用来测定距离的尾数；一个为粗测频率，“光尺”较长。用来测定距离的概略长度。

（二）国产DCJ—32—1型红外测距仪简介

图6-76是北京光学仪器厂制造的DCJ—32—1型红外测距仪，由TDJ2E型正像光学经纬仪和DGH3型红外测距仪组成，具有测角、测距以及计算坐标增量和高差等多种功能，可以进行跟踪测量和多个测回的平均值测量。单次测量和多次平均值测量的测距中误差为±5mm+5×10-6D（“+”号前是与距离无关的绝对误差，“+”后是与距离大小有关的相对误差）；跟踪测量的测距中误差为±10mm～±20mm+5×10-6D。精测频率为14985543Hz（赫兹），即“精测光尺”为10m；粗测频率为149855Hz，即“粗测光尺”为1000m。但通过增设在仪器内部的微处理机，实际测程可达0.2～5000m。此外，该仪器配有3块反光镜，最大只能测定3km的距离；如所测距离要达到5km，必须自备8块反光镜。

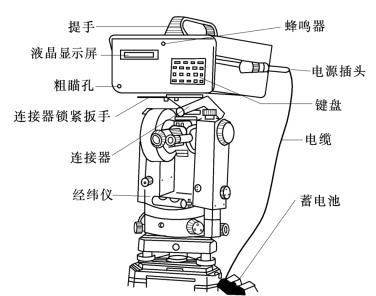
图6-76　DCJ—32—1红外测距仪

现将该仪器的有关按键、显示符号和使用方法说明于下。

1.按键功能和显示符号

测距仪的键盘（图6-77）上，除电源开关键ON（开）和OFF（关）以及数字键外，还有7个重要功能键：

（1）SIG 信号接收键。测距时，照准反光镜后，按此键检查光强。正常时，显示屏上出现7条虚线，同时显示“”符号，蜂鸣器响。

图6-77　DCJ—32—1型测距仪的键盘

（2）MEAS 距离测量键。测距时，按下此键，“”符号消失，蜂鸣器停响；至显示屏上出现7条实线时，测距完成（单次测量约10s），显示斜距。

（3）SET 数据输入选择键。需要输入气压、温度、天顶距和水平角时，须先断续按动此键，当显示屏上出现相应的数据符号（英文字母）后，停按此键，输入该项数据：V（天顶距）；H（水平角）；P（气压）；T（温度）。

（4）FUC 测量成果取出键。测距完后，断续按动此键，屏上逐一显示所需成果，并以相应符号告之是哪项成果：/Δ（斜距）；（平距）；Δ|（高差）；x（纵坐标增量）；y（横坐标增量）。

（5）STA 测量方式选择键。测距前，断续按动此键，选择所需测量方式，并在屏上显示相应的字母：M（在显示屏左下方）表示采用垂直反射器进行平均值测量；Tr表示跟踪测量；Sp表示采用可倾斜反射器的单次测量；SpM表示采用可倾斜反射器的平均值测量；不显示上述字母时，表示采用垂直反射器的单次测量。

（6）. 点键。有三种功能：①未输入数据前，按此键显示屏照明灯启亮；②在输入数据时，表示数据中的小数点；③当显示屏出现T，输入零下气温时，按此键为负号。

（7）CE 清除键。有两种功能：①未输入数据时，按此键则显示屏照明灯关熄；②输入了数据后，按此键清除数据。

此外，在仪器顶部右侧的护盖下，有一个供设置加常数和度量单位用的Bit开关：将6个上方注记“0”、下方注记数字的小开关分别推向不同位置，可组成所需的加常数（其值为各数之和，单位mm）；将两个上方注以F（距离英制）、G（角度400g制），下方注以M（距离m制）、D（角度360°制）的小开关分别推向不同位置可定出所需度量单位，并在显示屏上表示出来。

2.测量操作程序

（1）安置仪器。将经纬仪和反光镜分别安置在测站和镜站上，对中，整平；将测距仪与经纬仪连接一起，接上电源。

（2）照准目标。用望远镜和反光镜上的准星使主机与反光镜相互照准，将望远镜的十字丝中心对准反光镜的十字丝中心。

（3）检查仪器工作状态。按动ON键，仪器进行自检。正常时，屏上依次显示7个0，7个1…，直至7个8；否则，显示7个1。如果正常，再按动SIG键，检查光强。

（4）选择测量方式。断续按动STA键，当屏上出现所需测量方式字样时，停按此键。

（5）输入数据。断续按动SET，当屏上出现相应数据符号时，停按此键，输入相应数据。如果所输数据不合逻辑（如水平角大于360°）时，屏上显示H，并不停地闪烁，几秒钟后恢复原数据符号，可重新输入正确数据；如果自己发现输错数据，可按CE键清除重输。

为了求得坐标增量，在照准起始方向时，应使水平度盘置数等于起始方向的方位角，这样，照准待测点时的水平度盘读数即为方位角，将它输入仪器中。

（6）测量距离。按动MEAS键，约10s后，显示斜距。

（7）取出所需成果。按动FUC键，取出所需成果。其中高差须另外加仪高减觇标高，才是地面高差；否则，只是D ctg Z的值。

仪器有记忆功能，未重新测量前，成果可重复取出。

（8）测距结束。按OFF键，关机。

（三）全站仪测距

全站仪是由电子测角、光电测距、微型机及其软件组合而成的智能型光电测量仪器，它的基本功能是测水平角、竖直角和斜距，借助于机内固化软件，可以组成多种测量功能，如可以计算并显示平距、高差以及镜站点的三维坐标，进行偏心测量、悬高测量、对边测量、面积计算等。

全站仪测量距离特别方便快捷，精确度高，测距时，在镜站点竖立反射棱镜，仪站点照准反射棱镜，按动按键，立即在仪器显示屏上显示出距离，精确到毫米。现在的测量部门、施工工地都已采用了这种先进仪器。

（四）红外测距误差概述

红外测距误差大致分为两部分：一是与距离长短无关的固定误差；二是与距离长短有关的比例误差。这两部分误差的大小，在仪器说明书上都有说明。

1.固定误差

固定误差产生的原因主要有以下3个方面：

（1）对中误差。由于测站和镜站仪器对中不精确而引起对中误差。安置仪器时，应尽量精确对中。

（2）仪器常数校准误差。测距仪的常数，出厂前已经测定并输入仪器自动改正，但经过一段时期后会发生变化，引起测距误差。因此仪器常数应定期检定，如有变化，应加入剩余常数，以消除此项误差。

（3）测相误差。包括：①鉴相测相系统的读数差或数字相位计的原理误差，此误差与读数装置、鉴相灵敏度有关，须靠提高仪器本身的质量解决；②照准误差，由于发射光束在反光镜不同位置，引起相位不均匀产生此项误差，可采用“电照准”方法予以减小；③幅相误差，由于接收信号的强弱不同，引起此项误差，应按仪器说明书指定的范围控制信号的强弱，以减小这项误差（目前有不少测距仪安有自动控光装置，自动减小这种误差）；④周期误差，它依不同距离以光尺为周期重复出现，应通过定期检查发现它的变化情况，若变化过大，应送仪器工厂调整或检修。

测相误差具有偶然误差性质，可通过增加测回数减小其影响。

2.比例误差

（1）真空中光速值的测定误差。目前我国和世界各国都采用国际大地测量协会1975年第16届大会关于基本大地参数的决议中推荐的真空光速值：c0=299792485±1.2m/s，相对误差约为1/2.5亿。这项误差对测距的影响很小。

（2）大气折射率误差。测距时光在大气中传播的速度，是根据真空光速值和大气折射率求得的，而大气折射率又是根据测距时的大气温度、湿度、气压等因素确定的，所以上述各气象因素测定的精度和它们在距离上的代表性如何，将影响测距成果。为了减小气象因素影响所带来的测距误差，应选择良好的气象测量仪器，在稳定的有利气象条件下进行距离测量。

（3）调频误差。测距仪调制频率的精度和稳定性，影响“光尺”长度，从而给测距带来误差。为了减少以至消除这项误差，应交计量部门检定频率，必要时。在距离中加入频率改正数。

四、直线定向

确定某一直线与标准方向线的夹角，称为直线定向。直线定向是确定地面点平面位置的一项基本测量工作。

（一）标准方向

测量工作中常用的标准方向有真子午线、磁子午线与纵坐标轴（坐标子午线）。

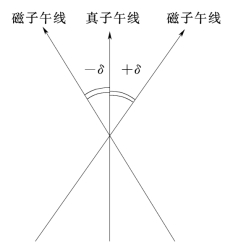
图6-78　磁偏角

真子午线可以通过观测北极星或其他星体予以确定。磁子午线是磁针静止时所指的南北磁极方向线，可用罗盘仪标定。真子午线和磁子午线分别向各自所指的两极收敛，因此，赤道上各点的子午线互相平行外，其余各地面点的子午线互不平行。同时，由于地磁两极不与地轴两极重合，致使磁子午线与真子午线之间形成夹角，称为磁偏角，以δ表示，如图6-78所示。磁子午线北端向东偏离真子午线，称为东偏，磁偏角为正。向西偏离真子午线称为西偏，磁偏角为负。磁偏角的大小因地而异，在同一地点因时间不同而有微小变化；我国磁偏角δ的变动范围约在+6°（西北地区）和-10°（东北地区）之间。

在普通测量中，常采用平面直角坐标系。故取纵坐标轴（x轴）或平行于纵坐标轴的直线作为标准方向。纵坐标轴又称坐标子午线。在独立测区，可取任一点的磁子午线作为纵坐标轴。

（二）方位角和象限角

从标准方向的北端开始，顺时针方向量至某直线的水平角称为方位角，以α表示，其值由0°～360°。方位角的名称与采用的标准方向相应，分别称为真方位角、磁方位角和坐标方位角。

图6-79表示磁方位角与真方位角之间的关系，即

图6-80表示以纵坐标轴为标准方向的坐标方位角。如果从A到B的方位角αAB为正方位角，则从B到A的方位角αBA称为反方位角。正、反方位角的关系为

直线与纵坐标轴最靠近的一端所夹的锐角，称为象限角，以R表示。象限角与方位角的关系如下

Ⅰ象限（北东）：R=α　Ⅱ象限（南东）：R=180°-α

Ⅲ象限（南西）：R=α-180°　Ⅳ象限（北西）：R=360°-α

图6-79　磁方位角与真方位角之间的关系

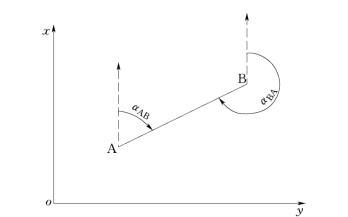
图6-80　坐标方位角及其正、反方位角

（三）磁方位角的测定

在独立测区，常用某直线的磁方位角作为整个测区定向的依据。磁方位角可用罗盘仪测定。有的经纬仪（如西北经Ⅲ型）上配有管式或长盒式指南针，管子（或长盒）中轴与望远镜视准轴相互平行，只有当望远镜指向磁北方向时，磁针才位于管子中轴线上；如果这时将水平度盘置零、再去照准另外的目标，即可从水平度盘上读出测站至该目标方向的磁方位角。

图6-81为地质测量常用的一种盒式罗盘仪，主要由磁针、刻度盘、水准器和照准器等部件组成；此外，还有供测坡度用的测斜度盘及其指标水准管。因为我国位于北半球，受北磁极的作用比南磁极强。为了不使磁针倾斜，在磁针靠南端缠有一段铜丝维持平衡。当揭开盒盖后，磁针制动钉自动弹起，磁针即自动指向南北磁极方向。照准器（即准星4）通过绞栓和刻度盘固连一起，随度盘一道转动。照准器的轴线（视准轴）通过度盘分划中心，度盘分划线自照准器接物端起按逆时针方向注记。当照准地面某目标时（应使罗盘圆水准器气泡居中），待磁针稳定后，其北端所指度盘读数即为测站至该目标方向的磁方位角。

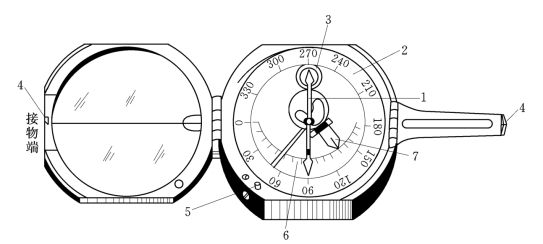
图6-81　地质罗盘仪

1—磁针；2—度盘；3—圆水准器；4—准星；5—磁针制动钉；6—测斜度盘；7—测斜指标

观测磁方位角时，应避免各种含磁物体接近罗盘仪。观测结束后，应立即固定磁针或盖上盒盖，以保护轴尖。

（四）（坐标）方位角的推算

在独立测区，通常只测定起始边的方位角，其他各边的方位角则根据相关的水平角进行推算。

如图6-82所示，从A至D是一条折线。设已知起始边AB的方位角为αAB，并在转折点B、C用经纬仪观测了折线左边的水平角（称为左角）βB和βC，则由图可以看出，BC边和CD边的方位角为

一般公式（即左角公式）为即：从转折点向前一点去的方位角，等于从后一点到转折点来的方位角加上转折点的左角，如果小于180°则加180°，大于180°则减180°（在减去180°之后若还大于360°再减360°）。

由于经纬仪的水平度盘是顺时针方向注记的，如果按照一般观测程序依点号顺次进行观测，先照准后视再照准前视，所测水平角总是前进方向的左角；如果沿着点号顺序进行观测时，先照准前视再照准后视，所测水平角就是右角。按右角推算方位角的公式为

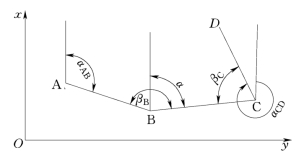
图6-82　（坐标）方位角的推算

不管是用左角或右角推算方位角，最好绘一个简图，据图推算就不易发生错误。

五、距离、方向与地面点直角坐标的关系

在测量上，x表示纵坐标，y表示横坐标，这种安排与数学上相反；方位角的量度方向和象限顺序也与数学上相反，但坐标计算却可应用现成的数学公式和符号法则。

下面介绍距离、方向与地面点直角坐标的关系。

（一）正算关系

根据平距和方位角计算平面直角坐标，称为坐标正算。

如图6-83所示，设A点的坐标为xA、yA，测得A、B间的平距为DAB，方位角为αAB，则B点的坐标xB、yB可用下述公式计算

式中　Δx——纵坐标增量；

　　　Δy——横坐标增量。

图6-83　距离、方位角与平面直角坐标的关系

坐标增量的符号系根据α所在的象限决定的，如表6-7所示。

坐标增量一般用电子计算器进行计算。计算器上通常都有增量计算专用程序键，键上标明P-R或x，y。具体操作因计算器不同而不同，但都是先输入边长，再输入方位角；显示时先显示Δx，最后显示Δy，同时显示出增量的符号。

（二）反算关系

根据两点的平面直角坐标计算它们之间的边长和方位角，称为坐标反算或边长方位角反算。

如果A、B两点的坐标xA、yA和xB、yB是已知的，则方位角、边长按下式计算

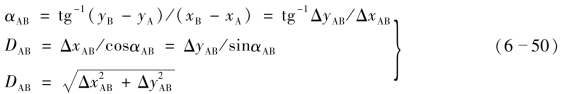
表6-7　方位角与坐标增量符号关系

在计算器上通常还有坐标反算专用程序键，键上标明R-P或rθ。具体操作因计算器不同而不同，但都是先输入Δx，再输入Δy；显示时总是先显示D，后显示α（以度为单位）。如果显示的α前带“—”号，说明此边在Ⅲ～Ⅳ象限，应加上360°才得方位角。如果不采用专用程序键，而直接接式（6-50）计算，则由反函数求得的角度为象限角R，应根据Δx、Δy的正负确定该边所在的象限，将象限角换算成方位角。