超低周疲劳断裂模型探究

众所周知，损伤与塑性变形密切相关，尤其对于延性金属更是如此。一般延性金属的应变强化可分为两种类型，即各向同性强化和随动强化。各向同性强化通常是由晶胞壁等稳定的位错结构的形成引起的，而随动强化主要是由具有不太稳定结构的位错引起的，如塞积位错（Yoshida and Uemori，2002）。各向同性和随动强化的定义如图10-12所示，使用延性金属在单轴循环加载下的典型应力-应变曲线。图10-12（a）显示了第5次反向加载时的应变强化效应可忽略不计，而第3次反向加载时会出现明显的应变硬化。主要原因是第3次反向加载时应变幅比第1次反向加载时增加了一倍，而第5次反向加载时应变幅相对第3次反向加载时基本保持不变。应变强化与材料的损伤密切相关，为了考虑不同的损伤累积速率，当等效塑性应变幅值相对于之前的幅值有所增加时，定义为各向同性相关损伤，其余部分则定义为随动强化相关损伤，如图10-12所示。

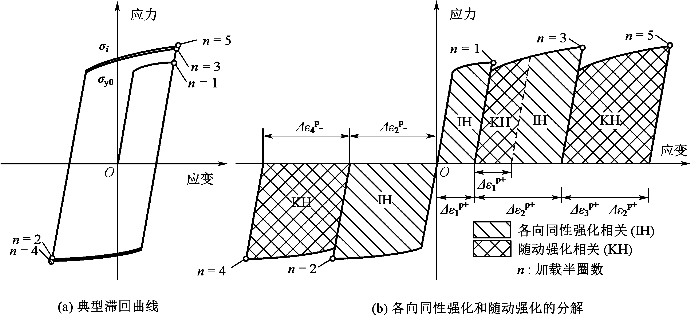
图10-12　各向同性和随动强化相关损伤的定义

裂纹萌生时刻的加载半圈数被定义为裂纹萌生寿命。CVGM模型大大低估了循环定幅加载下的裂纹萌生寿命，根据本章的定义，随动强化相关损伤在循环定幅加载下起主导作用。这意味着与随动强化相关的损伤被CVGM模型高估了。因此，本研究提出以下假定：

假定1：在相同应力三轴度的等效塑性应变增量下，各向同性强化引起的损伤累积大于随动强化引起的损伤。

假定2：随动强化引起的损伤累积与各向同性强化引起的损伤累积成正比。

假定3：各向同性强化相关损伤遵循CVGM模型的累积规律。

假定1很容易被接受，因为在许多金属的循环试验结果中都观察到了类似的结果（Kuroda，2002；Ohata and Toyoda，2004），试验和数值结果也证明了这一假设的合理性。

对于假定2，文献（Ohata and Toyoda，2004）中假定随动强化相关塑性加载历史不引起损伤累积，这个假定不太合理。因为根据文献中的损伤累积规则，延性金属在循环定幅加载下将永远不会发生断裂，而这与本章的试验结果不符。作为第一近似，本章假定随动强化相关塑性加载历史也会引起损伤累积，且引起的损伤累积与各向同性强化引起的损伤累积呈线性关系。

对于假定3，作者之前提出的CVGM模型对单调拉伸和循环加载工况采用相同的模型参数。对于单调拉伸，根据图10-12所示的定义，损伤累积都是各向同性强化相关的，且CVGM模型可以准确评估单调拉伸加载下的延性断裂问题，这意味着各向同性强化相关损伤是遵循CVGM损伤演化规则的。

根据上述假设，提出了以下损伤演化规律：

式中　D——总损伤；

D IH，D KH——分别为各向同性强化和随动强化相关损伤；

D CVGM——由CVGM模型定义的损伤指数；

η——材料常数。

与CVGM模型一样，当D达到1.0时，假设材料发生裂纹萌生。(www.xing528.com)

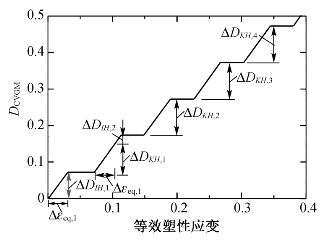
图10-13　各向同性和随动强化相关损伤的划分

根据式（10-1）—式（10-3），可在先前提出的CVGM模型的协助下预测超低周疲劳加载下延性金属试件的裂纹萌生，其中还有一项额外工作，即区分D IH和D KH。基于CVGM模型的双缺口试件的数值模拟结果，根据图10-13所示的方法区分损伤因子最大的节点的D IH和D KH分量，曲线的各上升段基本代表了节点的正应力三轴度相关加载历史，水平段代表了应力三轴度-1/3以下的加载历史，根据CVGM模型，应力三轴度-1/3以下时无损伤累积。从图10-13可看出，第1个拉伸加载半圈的损伤为100%各向同性强化相关，第2个拉伸半圈的损伤同时包含各向同性强化相关损伤和随动强化相关损伤，因为根据图10-12中的相关损伤定义，在第2个拉伸加载半圈中同时发生了各向同性和随动强化相关损伤。通过对比第1个和第2个拉伸加载半圈的等效塑性应变增量，可识别第2个拉伸加载半圈的D IH分量。对于除前两个加载循环外的后续加载历史，根据本章的定义相关损伤皆属于随动强化相关损伤。基于上述讨论，D CVGM的损伤增量可分为D IH和D KH两类，根据式（10-1）可得到总损伤因子。

基于上述超低周疲劳断裂模型，根据图10-14所示的流程图，可将超低周疲劳（定幅循环）加载下延性金属的裂纹萌生寿命与单调拉伸材性试验结果相关联，主要步骤如下：

步骤1：实施单调拉伸材性试验；

步骤2：对材性试验结果进行数值分析，对材料循环塑性模型参数和断裂模型参数进行标定；

步骤3：对定幅循环加载下试件的前三个加载循环进行数值分析，利用CVGM模型确定D IH和D KH的值，后继加载循环下的损伤均与第3个加载循环的损伤值相同；

步骤4：假设式（10-3）中的材料常数η已知，当D IH和D KH之和达到1.0时，可预测试件的裂纹萌生寿命。

在所提出的评估过程中，不需要对试件整个定幅循环加载历史进行数值模拟。图10-10所示的应力三轴度与等效塑性应变曲线表明，第3个加载循环的曲线几乎与后继加载循环的滞回曲线相同。因此，可使用第3个加载圈的曲线来表征后续的加载历史，仅需对前3个加载循环区分各向同性强化和随动强化相关的损伤增量。

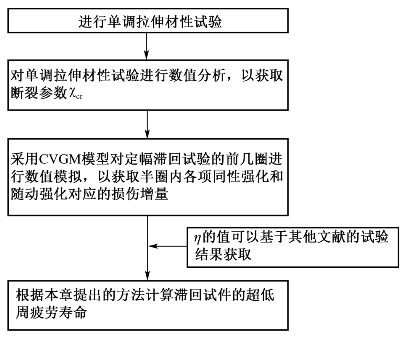
图10-14　单调拉伸材性试验结果及分析评估超低周疲劳寿命的流程图

对于η未知的情况，可通过对比所提超低周疲劳断裂模型预测的裂纹萌生时刻和试验结果的时刻，通过试错的方法即可确定该参数的值。本节采用所提的超低周疲劳断裂模型对铝合金6061-T6的试验结果进行模拟。η取为0.1～0.9，图10-15给出了根据式（10-1）—式（10-3）预测的裂纹萌生时刻、CVGM模型预测结果以及相关的试验结果的对比，当η取0.29时，预测结果和双缺口试件超低周疲劳试验结果对比最好；当η取1.0时，CVGM模型和本章所提的超低周疲劳断裂模型一样。图10-15（a）也表明，η的值对超低周疲劳寿命的评估结果影响显著。表10-4给出了所提超低周疲劳断裂模型（η取0.29）的预测结果与试验结果的对比，以及CVGM模型预测值与试验结果的对比。当η取0.29时，预测值与试验值比值的平均值为1.01，变异系数为0.094，表明该超低周疲劳断裂模型具有良好的评估精度。另一方面，与试验结果相比，CVGM模型大大低估了裂纹萌生寿命，预测值与试验值比值的平均值为0.36，变异系数为0.086。

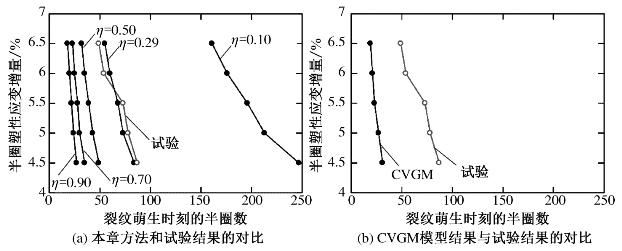
图10-15　超低周疲劳断裂模型与CVGM模型预测裂纹萌生时刻对比

表10-4　裂纹萌生时刻对应的加载圈数对比

备注：t Nini，ave为试验中裂纹萌生时刻的平均半圈数；
t Nini，theor为根据新提的超低周疲劳断裂模型预测的裂纹萌生时刻的平均半圈数；
t Nini，CVGM为CVGM模型预测的裂纹萌生时刻的半圈数。