基于力学性能的典型塑性模型参数标定方法

在塑性模型参数的标定过程中，通过两根材性试件的单调拉伸试验，获得所需的变量。由于假定β，εneck，γ1和k的值与双缺口试件相同（同牌号铝合金材料），因此在对Chaboche混合强化模型参数进行标定时，仅采用材性试验的典型力学性能参数。这与前述双缺口试件的塑性模型参数标定过程稍有不同，仅需要最小数量的机械性能参数，即材料的屈服强度和抗拉强度。根据新提出的标定方法，可以得到铝合金屈曲约束支撑的Chaboche模型参数值，如表9-2所示。同样，选择0.0～1.0范围内的β进行塑性模型参数的标定。

随着压缩变形的增加，屈曲约束支撑的芯棒在第一屈曲模态下开始屈曲，随后由于外套管的约束而不断发展为高阶屈曲模态。试验结果与数值结果的对比如图9-15所示。数值模拟可以较好模拟两个试件的变形模式。同时，还发现累积等效塑性应变可达300%左右，与机械等其他工程领域相比，极限应变相对较大。

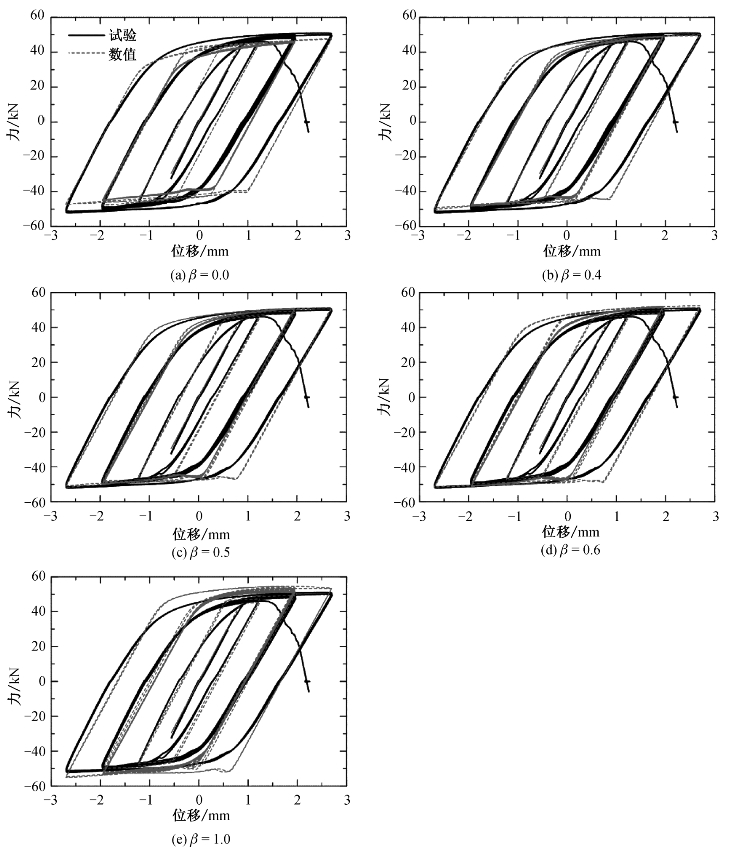
图9-16　试件S2-L4S20G1力-位移曲线的对比(www.xing528.com)

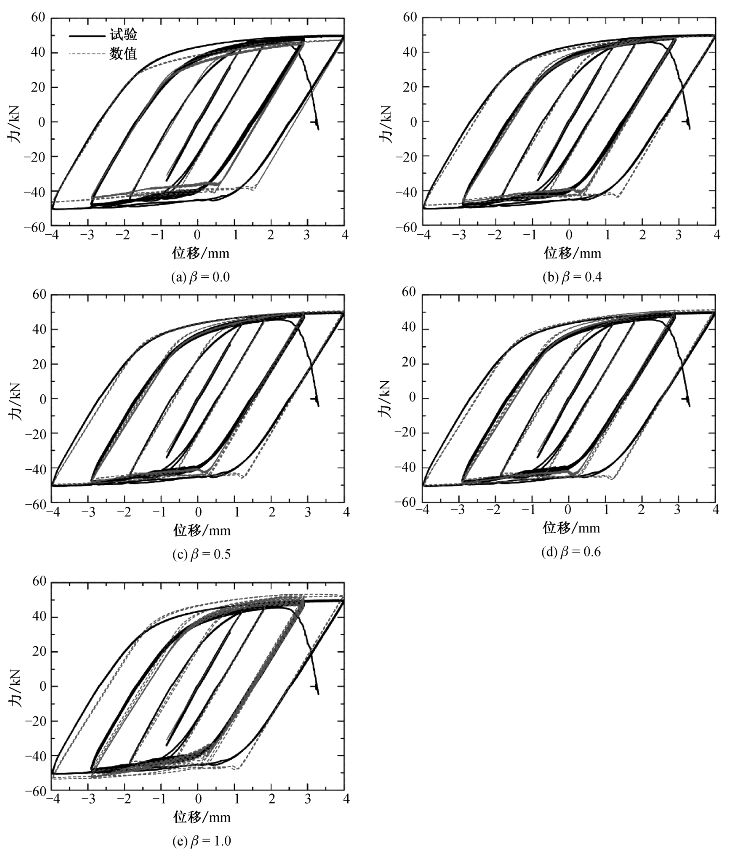
图9-17　试件S2-L6S20G1力-位移曲线的对比

图9-16和图9-17分别比较了试件S2-L4S20G1和试件S2-L6S20G1的试验和模拟结果的荷载-位移曲线。对比结果表明，利用所提出的标定方法得到的塑性模型参数，模拟精度良好。当β取0.5时可较好评估拉伸和压缩时的峰值荷载；当β取0.0和0.4时，有限元结果会低估了试验的峰值荷载；当β取0.6和1.0时，相应的值则高估了峰值荷载。因此，对于铝合金6061-T6，β的最优值在0.5附近。根据低碳钢的试验结果，β可作为一个材料常数，通常取0.5，与应变范围的关系不大。在实践中，如果没有可用的循环试验结果，建议β取0.5，并且该参数也可通过不同应变范围的循环试验结果进行标定。除第1个加载半圈外，弹塑性过渡区的应力仍被高估。这主要是由于在单调拉伸加载下的弹塑性转变区的硬化速率大于后续循环加载圈相应区域的硬化速率。