铝合金双缺口试件塑性模型参数标定方法

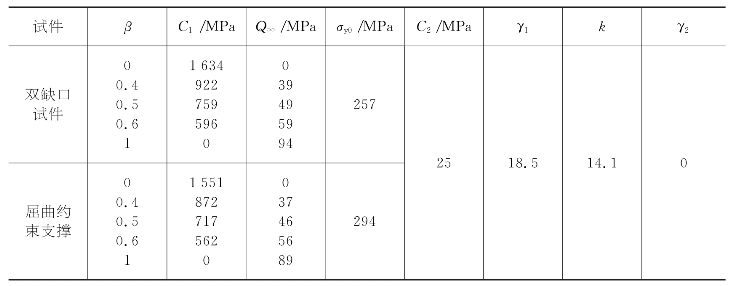
基于单调拉伸材性试验结果进行回归分析，以确定γ1，C 2和k的值，因为没有参考数据可用。确定的上述参数值和εneck可作为材料常数，并进一步用于铝合金屈曲约束支撑的分析。表9-2给出了铝合金6061-T6的γ1，C 2和k值，分别等于18.5 MPa，25 MPa和14.1 MPa。研究已经发现，对于大多数延性金属，如软钢和铝，β接近0.5，因此本研究选择0.0～1.0之间的值来研究结构铝6061-T6的最优值。对于不同的β，可根据上述标定方法得到C 1和Q∞，其值也在表9-2中给出。

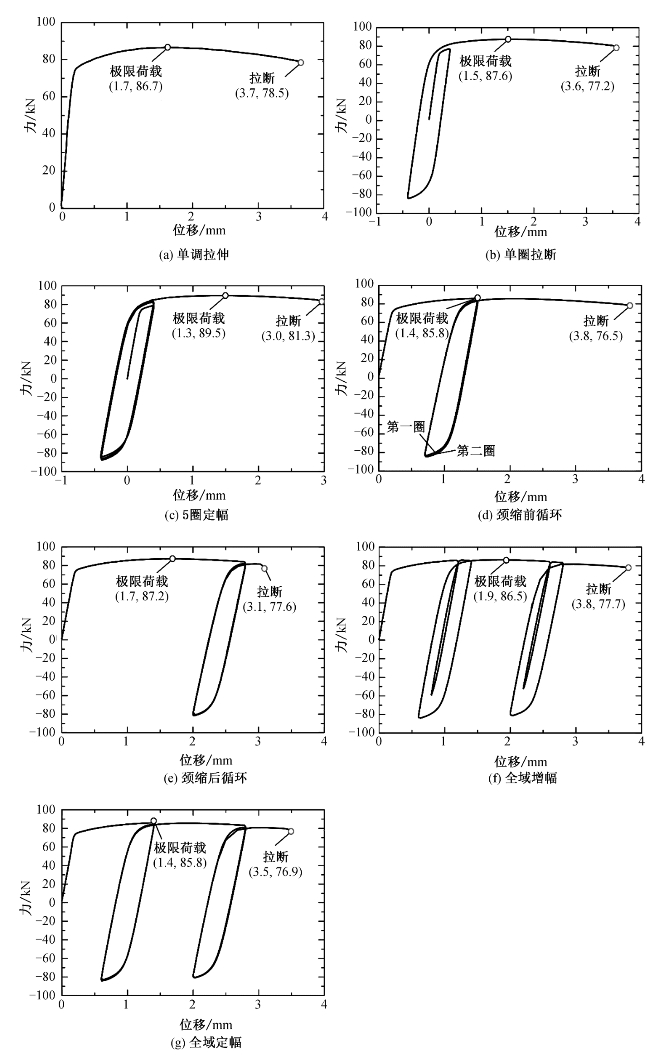
图9-8　双缺口试件的试验结果

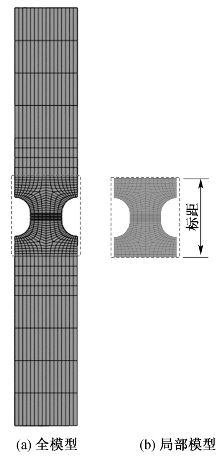
图9-9　双缺口试件局部模型和整体数值模型

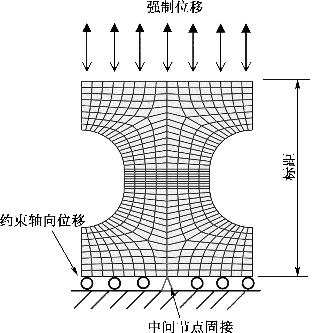
图9-10　双缺口试件有限元模型及边界条件

表9-2　塑性模型参数的标定结果

由数值结果得到的断裂时刻的等效塑性应变云图如图9-11所示，该图显示最小横截面的中厚处应变集中较明显。从图9-11可看出，相对于传统的金属塑性问题，本研究中大塑性循环加载下试件断裂时刻的等效塑性应变相当大，可达36%～64%。在颈缩后阶段，等效塑性应变急剧增加，且随着循环次数和加载幅值的增加而增加，例如5圈等幅循环加载。

图9-12给出了双缺口试件荷载-位移曲线的试验结果和数值结果之间的对比，其中，由于过早屈曲，未显示在单调压缩下的试验结果。从图中可得出以下结论：(www.xing528.com)

图9-11　断裂时刻的等效塑性应变云图（PEEQ：等效塑性应变）

（1）采用本章提出的标定方法，当β取0.4～0.6范围内的值时，Chaboche混合强化模型可较好地模拟结构铝6061-T6在单调拉伸和循环加载下的塑性行为。

（2）当β取0.0时，低估了试件的所有峰值承载力；当β取1.0时，高估了峰值承载力。

（3）对于图9-12（b）和（c）所示的小塑性应变范围，β取0.4时，Chaboche混合强化模型给出的评估结果最准确。

（4）在没有记忆面的情况下，Chaboche混合强化模型高估了等幅循环加载后续加载圈的应力，如图9-12（c）所示。

（5）对于图9-12（d）所示的中等塑性应变范围，即颈缩前定幅加载试件，β取0.5时，Chaboche混合强化模型对拉伸侧的评价结果最好，而压缩侧的β最优值为0.6。

（6）对于图9-12（e）至（g）所示的中、大塑性应变范围，即颈缩后等幅加载情况，β取0.5时，Chaboche混合强化模型对拉伸侧的评价结果最好，而压缩侧的β最优值为0.6。

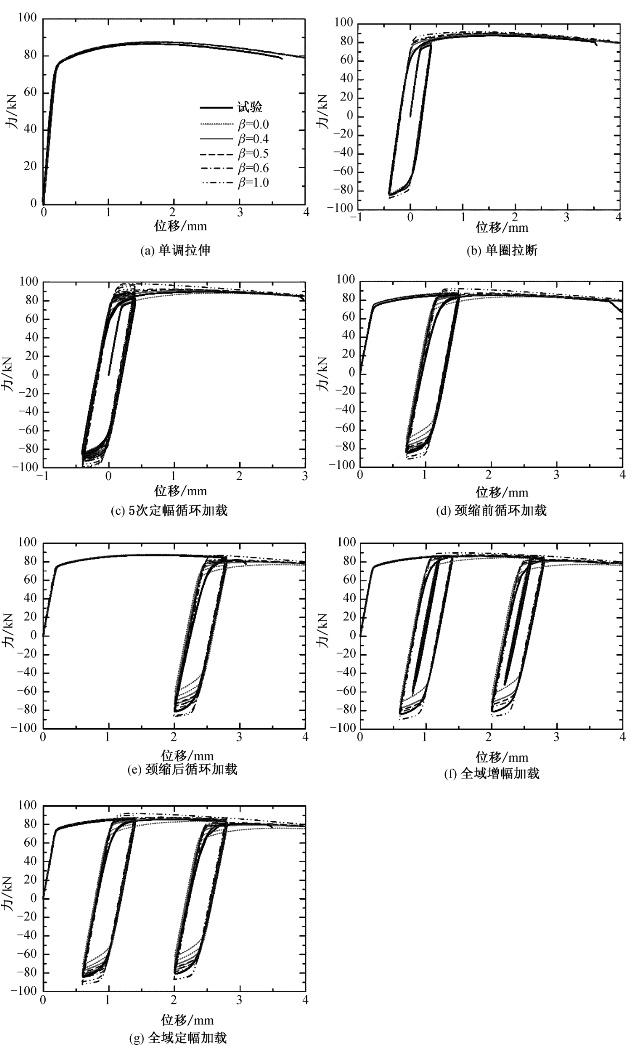
图9-12　双缺口试件试验和有限元结果滞回曲线的对比

（7）对于所有的循环加载工况，使用本章所提参数标定方法的Chaboche混合强化模型高估了弹塑性过渡区的应力。这主要是由于在弹塑性过渡区单调拉伸试验的硬化率高于循环加载下材料的屈服后硬化率（Yoshida and Uemori，2002）。