在之前的研究中(Jia and Kuwamura,2014b),作者发现循环塑性模型的参数,如Chaboche混合强化模型,可仅使用材料单调拉伸试验结果进行标定,这也得益于文献中疲劳试验的观察结果(Kuhlmann-Wilsdorf and Laird,1979)。因此,金属的循环塑性可以与相应的单调材性试验结果直接相关。在结构钢循环塑性研究中,在单调拉伸材性试验中,随动强化和各向同性强化分量几乎各占强化应力的一半。
对于单轴应力状态,Chaboche混合强化模型中背应力可表示为
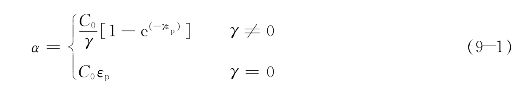
式(9-1)表明,当γ不等于零时,随动强化分量,即背应力的极限值为C 0/γ。
对于单轴应力状态,各向同性强化分量可表示为
![]()

图9-2 各向同性强化和随动强化在单调拉伸材性试验结果中的占比
同样的,各向同性强化分量的极限值为Q∞。对于Chaboche混合强化模型,必须确定初始屈服应力σy 0,随动强化相关参数,即Ci和γi,以及各向同性强化相关参数,即Q∞和k。
根据以下公式,总强化应力R+α可以很容易计算得到:
![]()
式中,σi是从单调拉伸材性试验中获得的真实应力。假设各向同性强化分量在总强化应力中的比例等于β,则R和α可按图9-2所示的方法得到:

在比较单调和循环试验结果的基础上,可得到β值,该参数可作为相同牌号金属材料的材料常数。一旦确定了β,就可以根据式(9-4)获得R与真实应变数据的对应关系,从而拟合得到Q∞和k。同样,也可根据式(9-5)获得α与真实应变数据的对应关系,且可简单通过回归分析获得Ci和γi。
对于Chaboche混合强化模型,必须确定以下模型参数:C 1,γ1,C 2,Q∞和k。根据式(9-4)、式(9-5),一旦确定了β的值,通过回归分析可以确定各向同性和随动强化相关参数。本章中,结构铝的随动强化分量采用了两个背应力。采用两个背应力的主要原因是其简单易行,可将塑性模型的参数与材料屈服应力、颈缩起始应变和抗拉强度等力学性能联系起来。对于随动强化分量,采用一个指数函数形式的背应力,另一个采用线性函数,即γ2为零。参数C 2与随动强化分量线性部分的硬化率相关,通常用于描述在大塑性应变范围内的硬化行为。在这些应变范围内,硬化速率可假定为线性关系。
为保证结构构件的极限强度评价准确,在标定过程中,材料在循环塑性模型中的抗拉强度应与单调拉伸材性试验结果一致。通常,材料的抗拉强度对应于颈缩起始的时刻。因此,拉伸材性试件颈缩起始时刻的随动强化和各向同性强化应力之和应等于材料颈缩起始时刻的强化应力。可得到以下方程:(https://www.xing528.com)
![]()
式中 σneck——颈缩起始时刻的真实应力;
R neck——颈缩起始时刻的各向同性强化分量;
αneck——颈缩起始时刻的随动强化分量。
σneck可由下式得出:
![]()
式中 sneck——颈缩起始时刻的工程应力,即材料的抗拉强度;
e neck——颈缩起始时刻的工程应变。
R neck可根据式(9-2)和式(9-4)得到:
![]()
式中,εneck为颈缩起始时刻的真实应变。
αneck可根据式(9-1)和式(9-5)得到如下:
![]()
通常,式中β,εneck,C 2,γ1和k可作为材料常数,对于同一等级的金属,这些常数的偏差较小。因此,Chaboche混合强化模型必须确定的参数为C 1和Q∞。对于铝合金等延性金属,假设已知β,εneck,C 2,γ1和k,一旦获得材料的屈服强度σy0和抗拉强度s neck,根据式(9-7)—式(9-9)可以很容易得到C 1和Q∞的值。
首先通过对铝合金双缺口试件的试验和数值研究验证了所提的标定方法的合理性,其中参数εneck,C 2,γ1和k由相应的材料拉伸材性试验结果获得。随后,利用铝合金屈曲约束支撑的试验结果在结构构件层面验证了所提方法的准确性,其中标定过程中仅使用材料的屈服强度和抗拉强度,因为εneck,C 2,γ1和k的值已经在之前的双缺口试件的试验和分析结果中确定。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




