节点域等效宽厚比对结构影响的分析

节点域等效宽厚比λpz对节点域的剪切稳定性能有较大影响，也被认为对试件的屈曲后延性断裂行为有影响。本节分析了3个不同λpz值的节点，即75，90和105，这些节点可能会发生节点域的剪切失稳。所分析节点的几何拓扑与试件H1n3相同，只有节点域的板厚有所不同。无量纲化的弯矩-转角曲线与相应的骨架曲线对比结果如图8-20所示，其中采用节点域的全截面塑性弯矩值对弯矩M进行了无量纲化。如图8-20所示的曲线表明，在0.06 rad大转角范围内，节点承载能力几乎不受影响，但随着λpz值的增大，滞回曲线的捏拢效应略微明显，超过0.06 rad转角时，节点的承载能力随着λpz值的增大而迅速减小。与初始几何缺陷尺寸的影响类似，λpz值对节点域裂纹萌生的影响也可忽略不计。如图8-20（b）所示，随着节点域等效宽厚比的增加，宏观裂纹的萌生时刻略为提前。

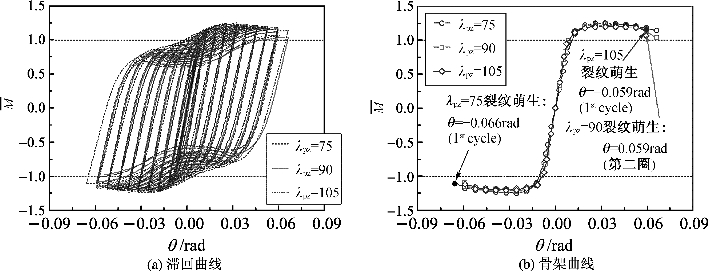
图8-20　节点域等效宽厚比的影响

(www.xing528.com)

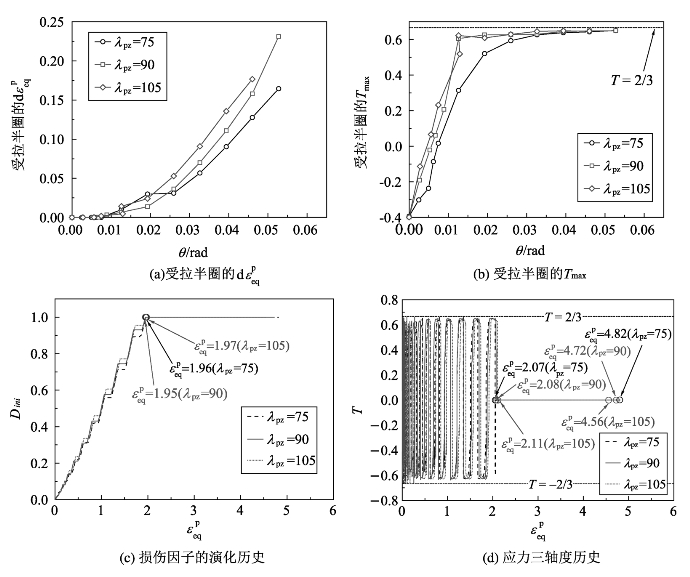
图8-21　节点域等效宽厚比的影响

为了进一步研究节点域等效宽厚比λpz对裂纹萌生时刻影响较小的原因，对不同λpz模型在每个拉伸加载半圈最初被删除单元的局部应力-应变状态进行了研究。图8-21（a）和（b）分别显示了不同λpz试件在每个拉伸半圈内等效塑性应变增量和最大应力三轴度T max与转角的相关关系。结果表明，随着λpz的增大，也随之增大，而3个模型的T max历史相似。根据本研究所采用的断裂模型，具有较大λpz的节点倾向于更早破裂。然而，图8-21（c）和（d）表明，对于具有不同λpz的3个节点，直至细观裂纹和宏观裂纹萌生时等效塑性应变的差异均在6%以内。3个试件在宏观裂纹萌生前的加载循环次数差异在一个位移幅值增量内，从整体性能上来看，影响并不明显。各加载半圈的正负应力三轴度峰值分别接近2/3和-2/3。为了分析最先被删除单元的应力状态，研究了被删除单元处材料的3个主应力。薄壁节点域处于平面应力状态，其中第一或第三主应力在最新被删除的单元处等于零。因此，此处的应力三轴度可以表示为

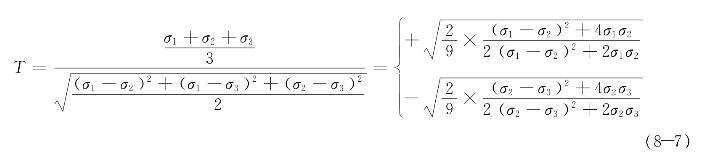
式中，σ1，σ2和σ3是3个主应力。式（8-7）的表达式显示当σ1=σ2时，T达到其最大值2/3；当σ2=σ3时，T达到其最小值为-2/3。通过数学推导可知，当σ2=0.563σ1时，T=0.6。这意味着，首先被删除单元的T可很容易达到最大值和最小值。这也解释了为什么在本研究分析的所有模型中，T总是趋向于收敛到上述两个常量值。