延性裂纹扩展的准则及应用探析

裂纹扩展准则是基于能量平衡的概念（Hillerborg，et al.，1976），该准则假定形成单位面积的裂纹表面需要吸收一定量的能量G c。在裂纹扩展过程中会释放一定量的储能，当释放的能量大于打开裂纹所需吸收的能量时，裂纹扩展。该方法与VGM相结合，可使用较大网格的单元模拟不含初始裂纹金属结构裂纹的萌生和扩展，而传统的断裂力学方法仅适用于裂纹尖端具有相当精细化网格且含初始裂纹连续体的裂纹扩展（Qian and Yang，2012）。可以定义裂纹扩展因子D prop：

式中　G——如图5-1所示细观裂纹萌生后单位面积所吸收的能量；

G c——裂纹表面单位面积吸收能量的阈值。

利用有效应力与裂纹宽度w 1之间的关系，可以从以下方程计算G c：

式中　w 1——当D prop达到1.0时对应的裂缝宽度；

σe——如图5-1所示的受损材料的有效应力。

与文献中提出的原始裂纹扩展规律不同（Hillerborg，et al.，1976），通过有效应力的概念来考虑材料劣化

(www.xing528.com)

式（5-4）假设有效应力随着D prop的增加线性减小。在有限元分析中，裂纹宽度可以基于特征单元长度l c的概念采用等效塑性应变描述。特征单元长度的定义取决于单元的几何和单元类型。对于梁和桁架等线单元，它是沿构件轴方向的特征长度；对于平面单元，它是面积的平方根；对于实体单元，它是单元体积的立方根。裂纹扩展损伤因子D prop也可由以下公式给出：

式中　——等效塑性应变；

——如图5-1所示细观裂纹萌生时刻的等效塑性应变，对应的Dini和D prop分别等于1.0和0。

这种处理可以减少有限元法的网格依赖性，从而可采用较大的单元模拟延性断裂问题。

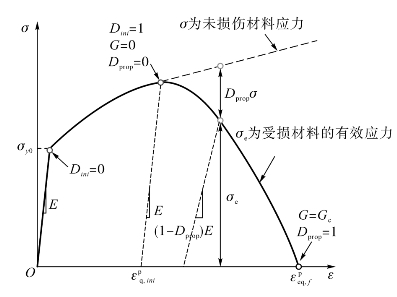
图5-1　单调加载下包含裂纹萌生和扩展准则的延性断裂模型示意图

考虑受损材料加载和卸载模量的退化，受损材料的弹性卸载模量可表示为

式中，E是未损伤材料的初始弹性杨氏模量。