改进的Yoshida-Uemori模型优化

1.Yoshida-Uemori模型的局限性

Yoshida-Uemori模型能够模拟大塑性应变范围内金属的循环塑性（Yoshida和Uemori 2002）。然而，该模型有几个局限性：

（1）研究发现，一些金属在材料断裂前呈现连续应变硬化而不会发生应力饱和现象（Shi，et al.，2008；Jia and Kuwamura，2014a）。在大塑性应变下，Yoshida-Uemori模型的各向同性强化分量往往会达到极限值，这可能导致在单调和循环加载下模拟某些结构钢塑性时产生相当大的误差。该模型可能会低估大应变范围内的应变硬化效应。

（2）该模型在应力空间定义了记忆面。然而，该记忆面的演化规则在特殊情况下会产生问题。根据式（3-18），β在单调加载下最终达到饱和值。根据式（3-23），q最终会渐进等于β，因为β保持不变。当β=q时，由式（3-22）可知，记忆面gσ的大小为零，即r=0，这使得无法确定记忆面的演化条件。导致当β达到饱和值时，回弹面的各向同性强化分量始终处于激活状态，即记忆面失效。如，当β在大应变范围内达到极限值时，各向同性强化分量将会一直增加，实际上大部分的金属材料在等幅加载下应力会逐渐达到饱和，在这种情况下应力会被高估。

（3）Yoshida-Uemori模型无法模拟屈服平台。由于背应力的演化规则是相互耦合的，因此该模型很难模拟具有屈服平台的结构钢。如果模型中没有很好地模拟出屈服平台，标定后的模型参数C可能无法通过拉伸材性试验得出低碳钢的准确结果，这也会影响其他参数的值。然而，Chaboche模型没有这个问题，因为其背应力都是相互独立的。

2.各向同性强化分量的修正

Yoshida-Uemori模型假定其回弹面各向同性强化分量的演化规则与Zaverl Jr等（Zaverl Jr and Lee，1978）提出的相同。在单轴应力状态下，Yoshida-Uemori模型的回弹面的大小可以表示为

可以发现，各向同性强化分量R趋于接近一个恒定的饱和值R sat。然而，在第2章中我们发现，随着塑性应变的增加，大塑性应变下的真实应力仍近似呈线性增加，不会发生应力饱和现象（Jia and Kuwamura，2014b）。因此，在改进的Yoshida-Uemori模型中，通过一个额外的线性强化函数与由Zaverl Jr和Lee（1978）提出的强化函数的叠加来避免原模型的局限性。

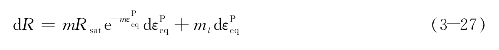
式中，m和m l为模型参数；大塑性应变下的强化速率由线性项的强化模量ml决定，而小塑性应变范围（例如颈缩开始前）下的强化速率由m和m l决定。

单轴应力状态下R的表达式如下：

由式（3-28）可知，本模型所采用的回弹面的各向同性强化分量的第一项在大塑性应变下会趋于饱和，而第二项在大塑性应变下仍呈线性发展，这与布里奇曼（1952）进行的高静水压下金属的断裂经典实验结果一致。

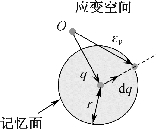
图3-6　Ohno提出的记忆面示意图

3.记忆面的修正

如图3-6所示应变空间中的记忆面，该记忆面由Ohno（1982）提出，它可保证回弹面的各向同性强化分量的演化条件始终处于可判定状态。应变空间中的记忆面表达式为(www.xing528.com)

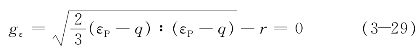
式中，q和r分别为记忆面的中心和半径。

类似的，记忆面gε的演化规则如下：

式中，q的初始值为0。

由记忆面gε的一致性条件可得：

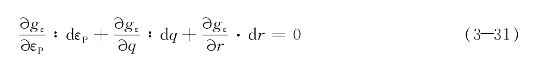
然后，

r的演化规则假定为

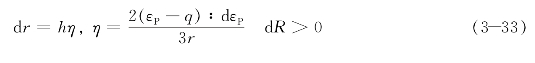
式中，h是确定记忆面gε膨胀速率的模型参数，r在d R＜0时不会改变。

根据式（3-33），如果当前应变状态在记忆面内或当前增量塑性应变张量与记忆面法向的夹角大于90°，则不会发生各向同性强化。利用这一假定，可以模拟金属在等幅加载下的应力饱和现象，而无记忆面塑性模型预测的等幅加载下的应力会继续增大，无法模拟应力饱和现象。

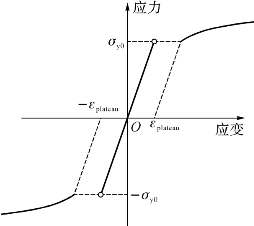
图3-7　屈服平台的修正

4.屈服平台的修正

屈服平台内的循环塑性行为非常复杂，Mahan等（Mahan，et al.，2011）对屈服平台进行了详细的模拟。Yoshida和Uemori（2002）提出了一个模拟屈服平台的简化方案。该模型在应力空间中定义了一个屈服平台，导致很难定义与屈服平台大小相关的模型参数。在此，假设当等效塑性应变小于用标量εplateau表示的屈服平台尺寸时，不会发生硬化，如图3-7所示。此条件定义为