改进的Yoshida-Uemori模型

Yoshida-Uemori模型是一个双面循环塑性模型。该模型是一个相对较新的模型，但已经被嵌入到LS-Dyna等一些有限元软件中。它是一个具有固定尺寸的屈服面和变化尺寸的回弹面的混合强化模型。具有Mises屈服函数模型的屈服面可以表示为

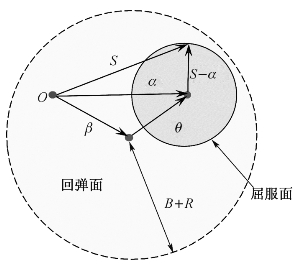
图3-4　Yoshida-Uemori模型的屈服面和回弹面示意图

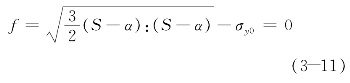
如图3-4所示，其回弹面的函数F可以表示为

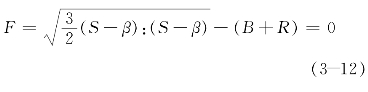
式中　β——代表原点到回弹面的中心；

B，R——分别是回弹面的初始尺寸以及其各向同性强化分量。

屈服面和回弹面的相对随动强化分量为

即

屈服面和回弹面之间相对随动强化分量的演化规则为

式中　C——模型参数；

——定义如下：

a——定义如下：

β的演化规则假定如下：

式中，m是模型参数。

将式（3-15）和式（3-18）代入式（3-14），可得：(www.xing528.com)

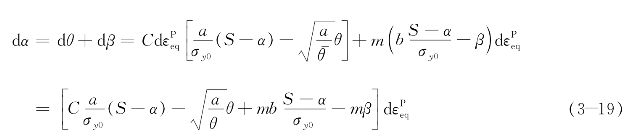
回弹面的各向同性强化分量的演化规则假定如下：

单轴应力条件下回弹面上的应力峰值可表达为

式中　R sat——非常大塑性应变下回弹面的饱和值；

——β的范数。

其中还有一个非各向同性强化面，用于记忆强化历史。非各向同性强化面通常称为记忆面，可模拟加工硬化停滞的现象，记忆面gσ定义为

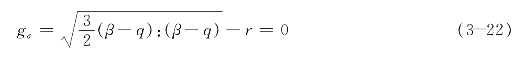
式中，q和r分别是记忆面的中心和半径。

记忆面gσ相对原点的移动定义为

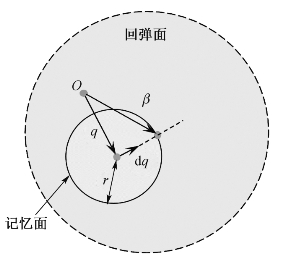
图3-5　Yoshida-Uemori模型记忆面的示意图

由记忆面gσ的一致性条件可得

r的演化规则假定为

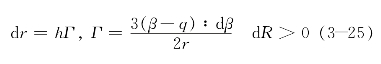
式中，h为模型参数，决定了记忆面gσ的膨胀速率。

记忆面如图3-5所示。为解释7个模型参数各自的功能，各参数的物理含义如表3-1所示，文献中也给出了单轴循环加载下参数的示意图（Yoshida and Uemori，2002）。

表3-1　Yoshida-Uemori模型各参数的物理含义