【摘要】:如图2-5所示,本数值分析采用ABAQUS中的CAX8轴对称单元,建立了材性试件的1/4有限元模型。数值分析仅模拟了标距内具有均匀截面的部分,并在左端施加对称的边界条件,右端采用位移加载。图2-5有限元模型的网格划分对于具有与试件相同名义几何尺寸的理想对称数值模型,很难模拟出颈缩的行为,因为数值模型会一直均匀伸长而不发生颈缩变形。加权平均法和修正加权平均法的加权因子ω数值分别为0和0.425。
如图2-5所示,本数值分析采用ABAQUS中的CAX8轴对称单元,建立了材性试件的1/4有限元模型。数值分析仅模拟了标距内具有均匀截面的部分,并在左端施加对称的边界条件,右端采用位移加载。采用ABAQUS非线性各向同性强化模型进行了分析。屈服准则是Mises屈服函数,流动准则为关联流动法则,这些在金属材料中是常用的。
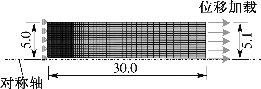
图2-5 有限元模型的网格划分(单位:mm)
对于具有与试件相同名义几何尺寸的理想对称数值模型,很难模拟出颈缩的行为,因为数值模型会一直均匀伸长而不发生颈缩变形。为了模拟颈缩,沿试件纵向方向给有限元模型一个较小的楔形几何缺陷,如图2-5所示。试样中心截面的半径为5.0 mm,而均匀部分的末端半径增加至5.1 mm。由于坡度只有0.33%,不会对整体力-位移曲线产生明显的影响。值得注意的是:颈缩处的应力状态是三轴的,数值模拟结果并不是试验应力-应变曲线的复制。(https://www.xing528.com)
通过简单修正法、加权平均法和修正加权平均法得到的真实应力-真实应变曲线如图2-6所示。颈缩时的真实应力和真实应变分别为558 MPa和0.20。加权平均法和修正加权平均法的加权因子ω数值分别为0和0.425。对于本试验,加权平均法得到的真实应力-真实应变数据恰好是其下限,即曲线可由幂函数表达。
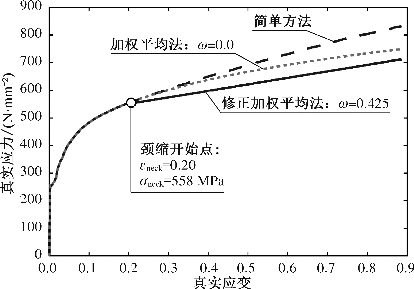
图2-6 三种颈缩后修正方法得到的真实应力-真实应变对比
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




