简单不对称故障的分析和计算

电力系统简单不对称故障包括单相接地短路、两相短路、两相接地短路、单相断线及两相断线等，其主要的分析方法为对称分量法。

如图6-7所示，当系统在f点发生不对称短路时，以a相为例，用代替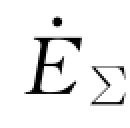，表示f点正常时的电压，根据其简化的正序、负序及零序网络可知，故障点处的三序电压平衡方式方程为

图6-7　a相接地短路示意

下面结合各种简单不对称短路及断线情况，分析其电流和电压的特点。取流向短路点的电流方向为正方向，选取a相正序电流作为基准电流。

1.单相接地短路

短路点f的边界条件为

将电压用正序、负序、零序分量表示为

由式(6-22)得a相电流的各序分量为

因此，用序分量表示的短路点边界条件为

工程上常采用复合序网的方法进行不对称故障的计算。结合故障类型，绘制出正序、负序及零序网络，利用故障点边界条件的序分量形式，将各序网络在故障端口联系起来，构成复合序网络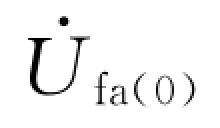，为故障前a相电压。依据表达式(6-27)的边界条件制定的单相接地短路的a相复合序网络如图6-8所示，各序网络串接，满足各序电流相等的条件。

从复合序网络可知

因此，短路点的故障相电流为

图6-8　a相接地短路复合序网络

同理

图6-9　a相接地故障处电压、电流相量图

图6-10　b、c两相短路示意

2.两相短路

设系统在f处发生两相(b、c相)短路(f(2))，如图6-10所示。

短路点的边界条件为

非故障相电流的正、负、零序分量为

即

说明发生两相短路时，无零序电流的通路，x0∑→∞。

可见，用序分量表示的短路点边界条件为

由此，绘制两相短路时的复合序网络如图6-11所示，正序网络与负序网络在故障点处并联，无零序网络。

从复合序网络可以直接求出正、负序电流分量为

利用序分量求得b、c相短路时各相电流为

图6-11　b、c两相短路复合序网络

短路点f处a相电压的序分量为

短路点的各相电压为

若x1∑＝x2∑，则有

式(6-37)表明非故障相电压在短路前后不变，故障相电压幅值降低1/2。(https://www.xing528.com)

3.两相短路接地

设系统在点f处发生两相(b、c)短路接地(f(1))，如图6-12所示。短路点的边界条件为

其各序分量间的关系为

式(6-39)为b、c两相短路接地时的序分量形式的边界条件。满足该边界条件的复合序网络如图6-13所示，即三个序网络在故障点并联。

图6-12　b、c两相短路接地示意

图6-13　b、c两相短路接地复合序网络

从复合序网络可以方便地求得非故障相(a相)电流及电压的各序分量，即

短路点的各相电流可由序分量合成得到，即

故障相电流的有效值为

如果x1∑＝x2∑，令k＝x0∑/x2∑，上式可化为

分析以下3种情况：

由故障相流入大地中的电流为

三相零序电流分量通过大地形成回路。

通过复合序网求得短路点处电压的各序分量为

因此，短路点处故障相电压为

非故障相电压为

若x1∑＝x2∑，非故障相电压为

分析以下3种情况：

(1)当k＝0，即x0∑＝0时，非故障相电压为0；

4.正序等效定则的应用

结合以上3种不对称短路情况下短路电流正序分量的计算，即式(6-28)、式(6-34)、式(6-40)，可以发现a相电流正序分量具有如下规律，即

表6-4　简单短路的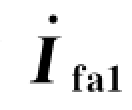、及

简单不对称短路电流的计算步骤如下：

(1)根据故障类型，做出相应的序网；

(2)计算系统对短路点的正序、负序、零序等效电抗；

(3)计算附加电抗；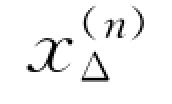

(4)依据式(6-47)计算短路点的正序电流；

(5)依据式(6-48)计算短路点的故障相电流；

(6)进一步求得其他待求量。

如果要求计算某时刻的电流(电压)，可以在正序网络中的故障点f处接附加电抗，然后应用计算曲线，求得经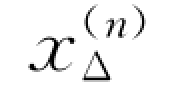发生三相短路时任意时刻的电流，即为f点不对称短路时的正序电流。