牛顿-拉夫逊法潮流计算的详细过程

牛顿-拉夫逊法潮流计算的步骤如下。

(1)形成网格的节点导纳矩阵YB。

(6)求各节点电压新的初始值，即修正后值

或

(7)利用事先给定的收敛标准判断收敛与否，即是否满足

(8)如不收敛，将各节点电压迭代值作为新的初始值自第(3)步开始进入下一次迭代。

(9)计算收敛后，计算各线路中的功率分布及平衡节点注入功率，PV节点注入无功功率。其中，平衡节点功率为

支路功率为

式中，yi0、yij、yj0分别为支路i端对地导纳值、支路导纳值和节点j端对地导纳值。

线路上功率损耗为

PV节点注入无功功率为

或

牛顿-拉夫逊法潮流计算流程如图3-13所示。

图3-13　牛顿-拉夫逊法潮流计算流程

图3-14　例3-4网络图

例3-4 某三节点系统如图3-14所示。线路阻抗标幺值已标明在图上，负荷功率的标幺值为：SL1＝1＋j0.5，SL3＝1＋j1，PG2＝1.5。节点3装有无功补偿装置，在运行时，各节点电压幅值U1＝U2＝U3＝1.0，节点1为平衡节点，用牛顿-拉夫逊法计算潮流，并计算出QC3、QG2及线路功率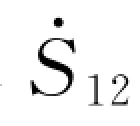。收敛精度ε＝10－3。

解：将网络化简，如图3-15所示，判断节点类型。

图3-15　例3-4网络简化图

第二步：设定电压初值，即

第四步：求雅可比矩阵，即

第五步：计算各节点电压的一次近似值，即(www.xing528.com)

返回第三步，重新迭代。

第二次迭代：

已满足收敛要求。

平衡节点功率为

②采用极坐标形式。

未知量为θ2、θ3，已知量为P2、P3。

第一步：形成节点导纳矩阵YB，即

第二步：设定电压初值，即

第三步：计算功率不平衡量，即

第四步：求雅可比矩阵，即

第五步：求修正量，解修正方程，即

解得

第六步：计算节点电压的一次迭代解，即

返回第三步重新迭代。

第二次迭代：

此时

已满足收敛要求。

第七步：电压解为

其结果与直角坐标的结果是一致的。