组合体的接合形式与相贯线形状分析

讨论组合体的组合形式，关键是搞清相邻两物体间的接合形式，以便于分析接合处两物体分界线的投影。

1.共面与非共面

画这种组合形式的视图时，应注意区分分界处的情况。如图3-2a所示，当两物体的邻接表面不共面时，在两物体的连接处应有交线，如图3-2a所示。其正确画法如图3-2b所示。

如图3-3a所示，当两物体的邻接表面共面时，在共面处没有交线。其正确画法如图3-3b所示。

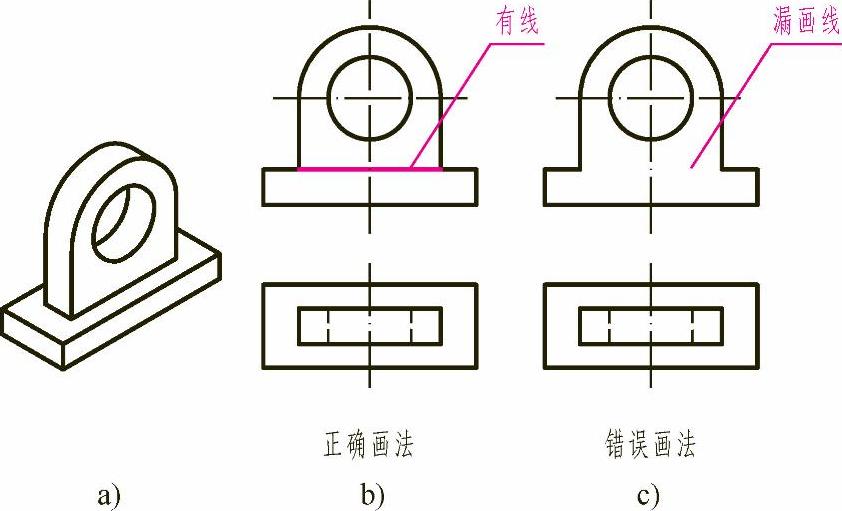
图3-2 两体表面不共面时的画法

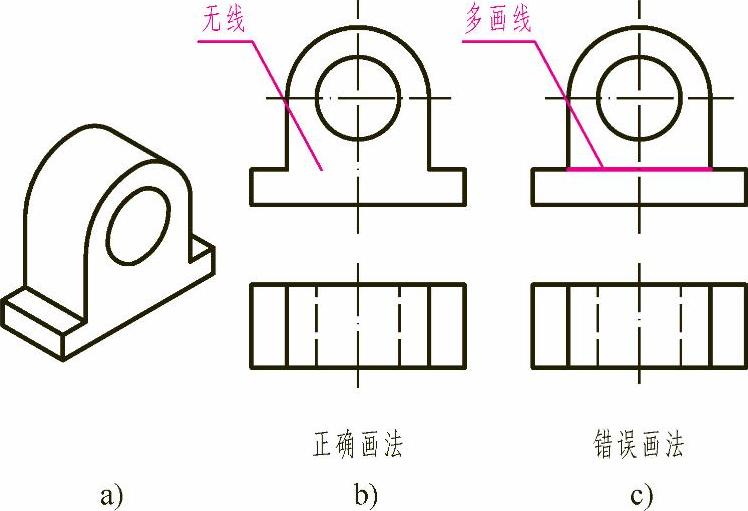
图3-3 两体表面共面时的画法

2.相切与相交

图3-4a所示组合体由耳板和圆筒组成。耳板前后两平面与左右两大小圆柱面光滑连接，即相切。在水平投影中，表现为直线和圆弧相切。在正面和侧面投影中，相切处不画线，耳板上表面的投影只画至切点处，如图3-4b所示。图3-4c是在相切处画线的错误示例。

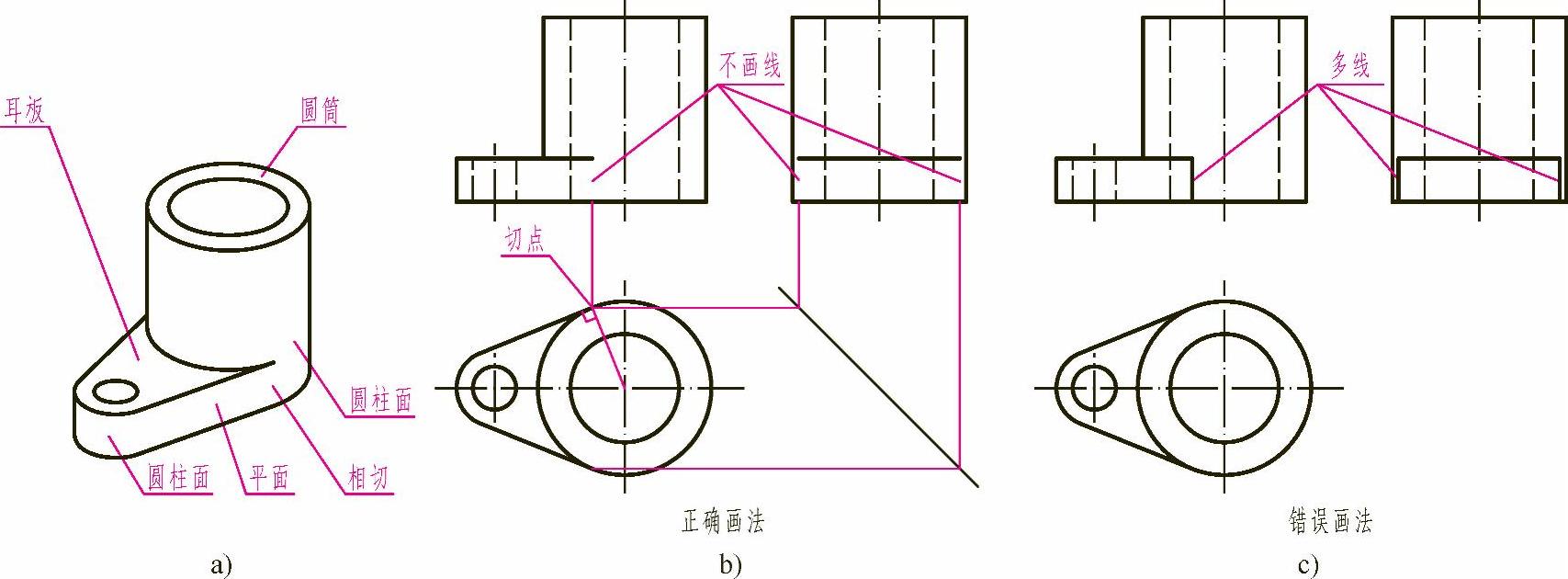
图3-4 两体表面相切的画法

图3-5a所示组合体也是由耳板和圆筒组成，但耳板前后两平面平行，与左右两大小圆柱面相交。在水平投影中，表现为直线和圆弧相交。在正面和侧面投影中，应画出交线，如图3-5b所示。图3-5c是在相交处漏画线的错误示例。

3.相贯

两回转体的表面相交称为相贯，相交处的交线称为相贯线。由于两相交同转体的形状、大小和相对位置不同，相贯线的形状也不同。相贯线具有下列基本性质。

①共有性。相贯线是两回转体表面上的共有线，也是两回转体表面的分界线，所以相贯线上的所有点，都是两回转体表面上的共有点。

②封闭性。一般情况下，相贯线是封闭的空间曲线，在特殊情况下是平面曲线或直线。

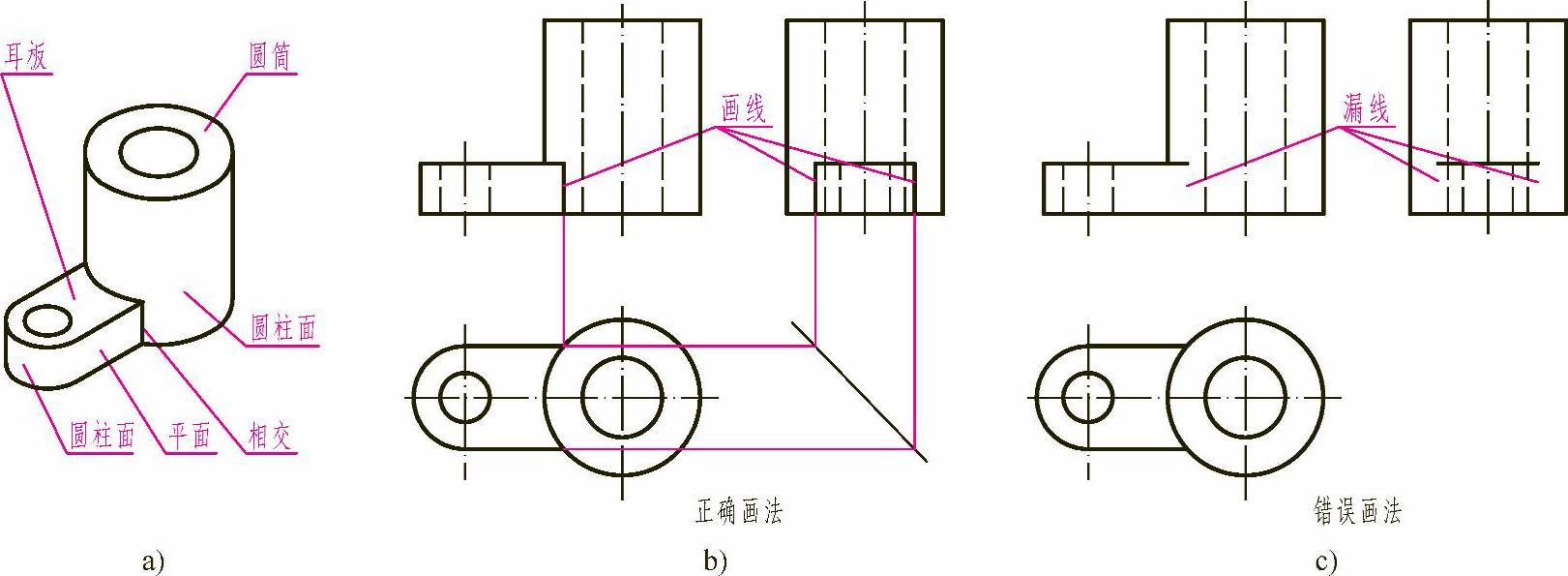
图3-5 两体表面相交的画法

（1）相贯线的简化画法 为了简化作图，国家标准规定，当不需要准确求作两圆柱正交相贯线的投影时，允许采用简化画法作出相贯线的投影，即用圆弧代替非圆曲线。

【例3-1】 如图3-6 a所示，两圆柱异径正交，用简化画法补画主视图中所缺的相贯线。

分析

由于两圆柱的轴线垂直相交，相贯线是一条前后、左右对称，闭合的空间曲线，如图3-6b所示。小圆柱的轴线垂直于水平面，相贯线的水平投影为圆（与小圆柱面的积聚性投影重合），大圆柱面的轴线垂直于侧面，相贯线的侧面投影为一段圆弧（与大圆柱面的部分积聚性投影重合），只需补画相贯线的正面投影，如图3-6c所示。

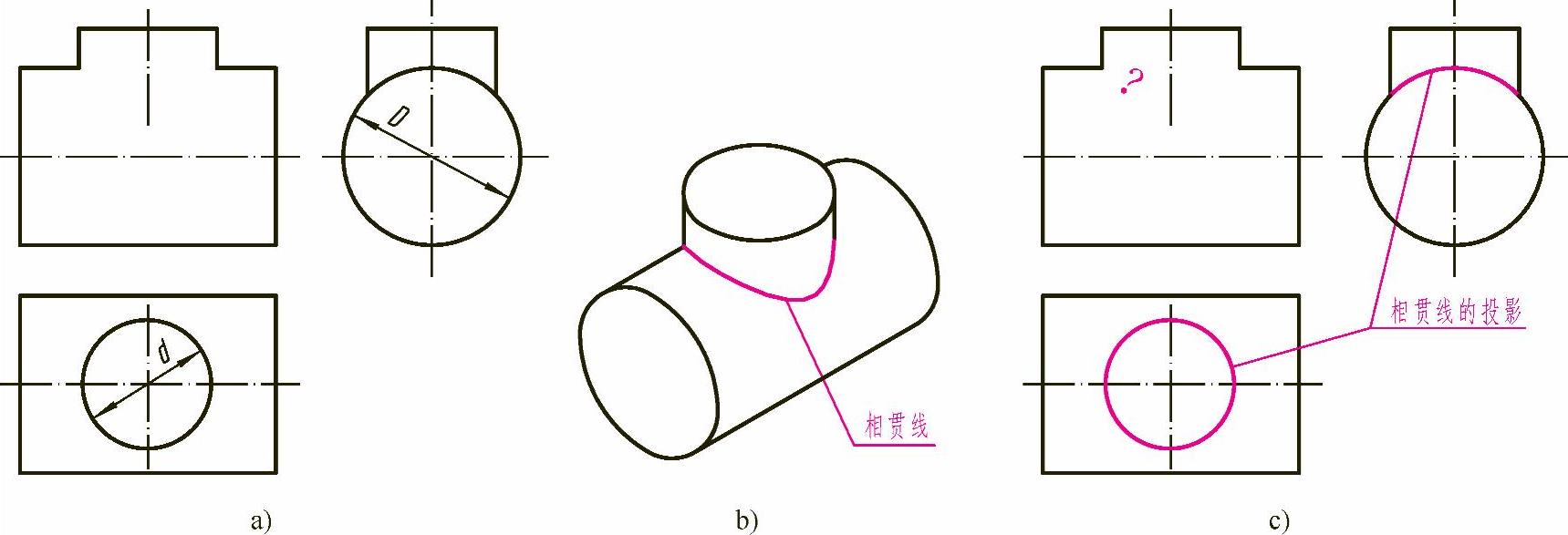
图3-6 两圆柱正交相贯线的分析

此时，相贯线的简化画法有以下两种方法。

第一种简化画法

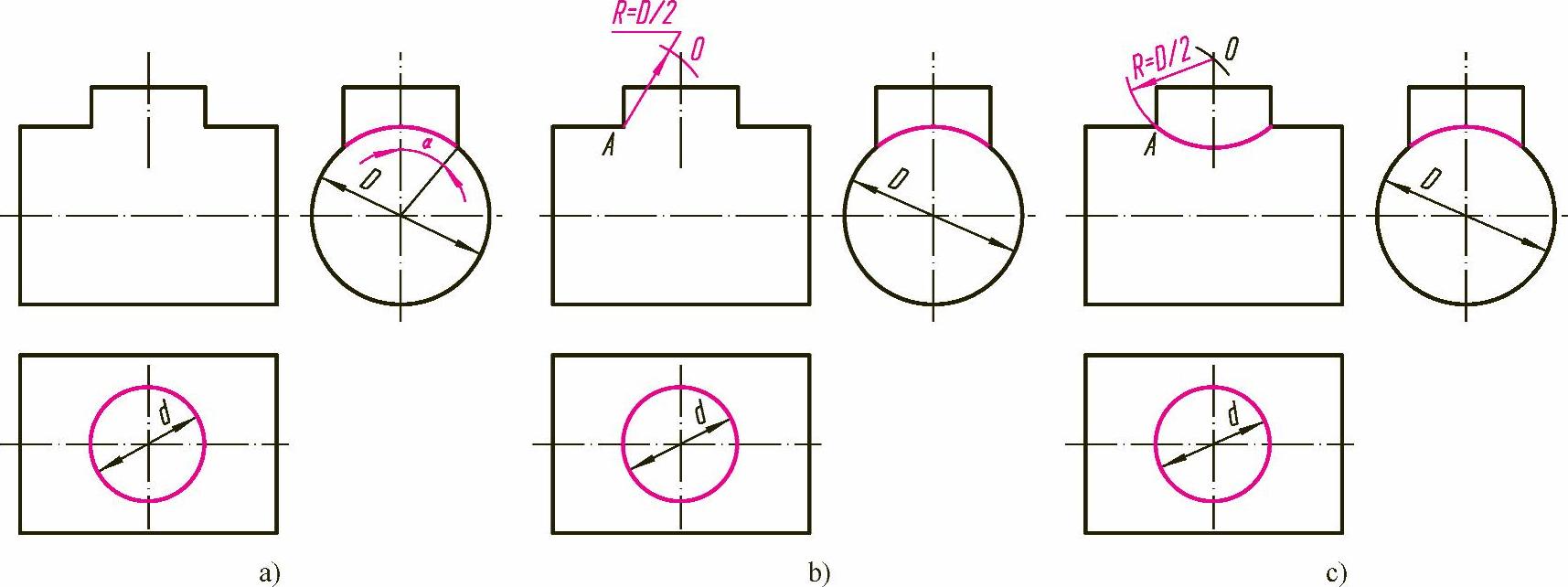
如图3-7a所示，当α≤45°时，可采用第一种简化画法，此种画法最为简捷。当α＞45°时，不能采用第一种简化画法（此时，所画圆弧与相贯线差别过大）。

①以D/2为半径、点A为圆心向上画弧得点O，如图3-7b所示。

②再以点O为圆心、D/2为半径画弧即可，如图3-7c所示。

(www.xing528.com)

图3-7 两圆柱正交相贯线的简化画法（一）

第二种简化画法

第二种简化画法虽然比第一种简化画法稍微复杂一些，但不受45°的限制，所画圆弧与相贯线比较接近。

①先求出相贯线的最低点K，如图3-8a所示。

②作AK的垂直平分线，与轴线相交得点O，如图3-8b所示。

③以点O为圆心、OA为半径画弧即可，如图3-8c所示。

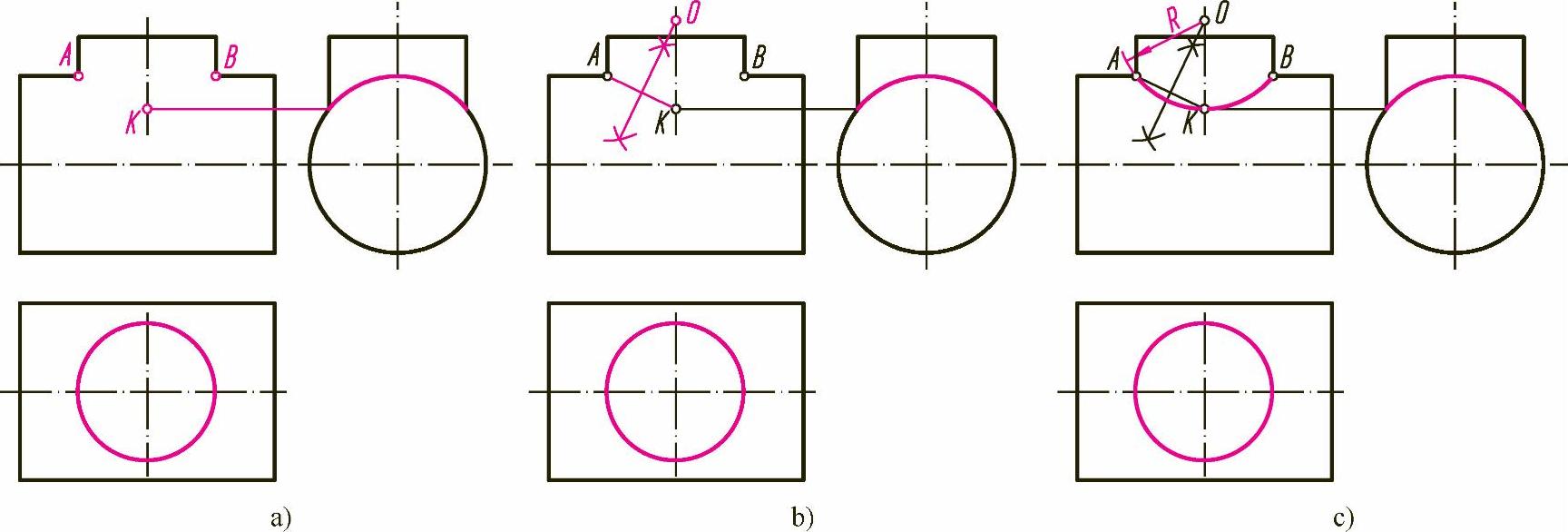
图3-8 两圆柱正交相贯线的简化画法（二）

（2）两圆柱正交时相贯线的变化 当两圆柱的相对位置不变，而两圆柱的直径发生变化时，相贯线的形状将随之变化。

当ϕ₁＞ϕ时，相贯线的正面投影为上、下对称的曲线，如图3-9a所示。

当ϕ₁=ϕ时，相贯线在空间为两个相交的椭圆，其正面投影为两条相交的直线，如图3-9b所示。

当ϕ₁＜ϕ时，相贯线的正面投影为左、右对称的曲线，如图3-9c所示。

提示：从图3-9a、c的正面投影中可以看出，两圆柱正交时相贯线的弯曲方向，朝向直径较大的圆柱。

（3）内相贯线的画法 当两个圆筒相贯时，则圆筒外表面及内表面均有相贯线，如图3-10a所示。

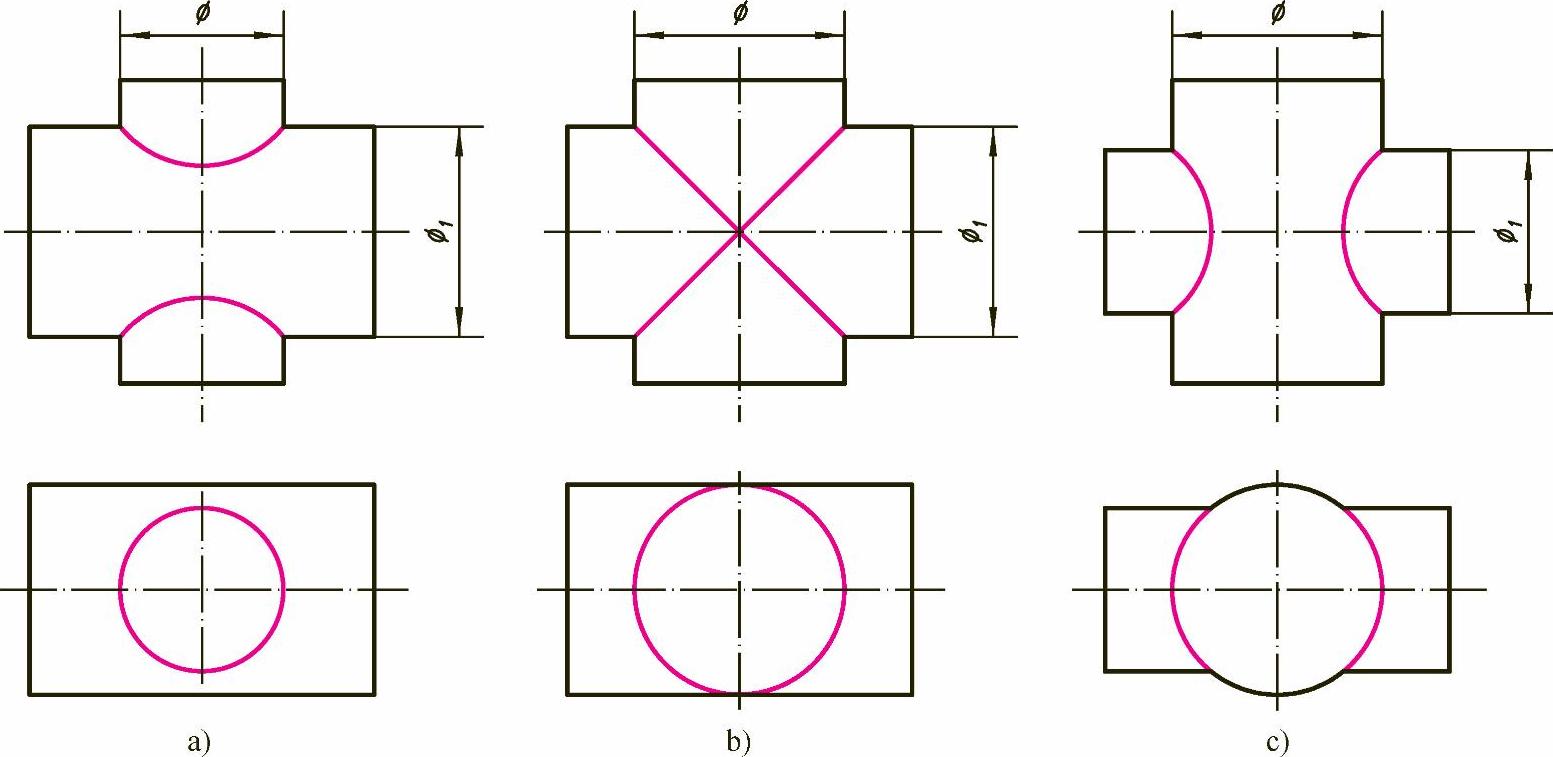
图3-9 两圆柱正交时相贯线的变化

在内表面产生的交线，称为内相贯线。内相贯线和外相贯线的画法相同，因为内相贯线的投影不可见而画成细虚线，如图3-10b所示。

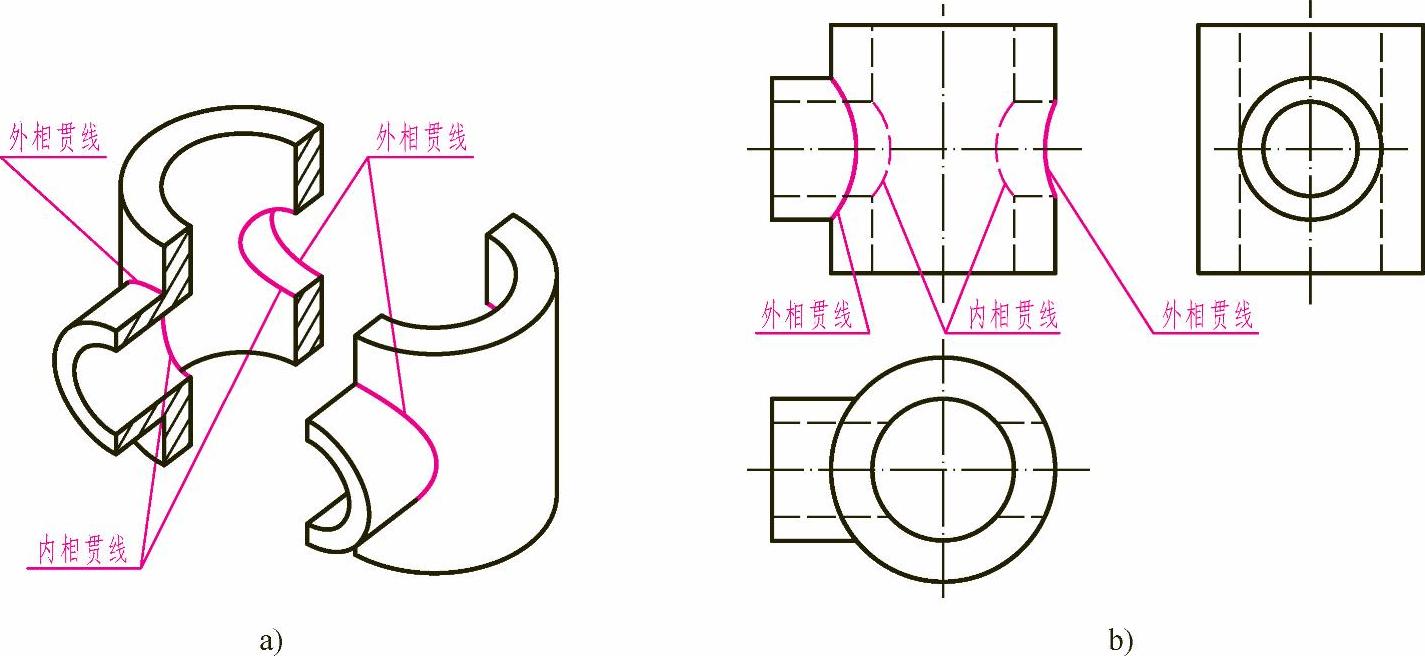
图3-10 圆筒相贯时相贯线的画法

（4）相贯线的特殊情况 两回转体相交，在一般情况下相贯线为空间曲线，但在特殊情况下，相贯线为平面曲线或直线。当两个同轴回转体相交时，相贯线一定是垂直于轴线的圆。若回转体轴线平行于某一投影面时，这个圆在该投影面上的投影为垂直于轴线的直线，如图3-11所示。

4.切割型

对于不完整的形体，以采用切割的概念对它进行分析为宜。如图3-12a所示的物体，可看成是长方体经切割而形成的，如图3-12b所示。画图时，可先画出完整长方体的三视图，然后逐个画出被切部分的投影，如图3-12c所示。

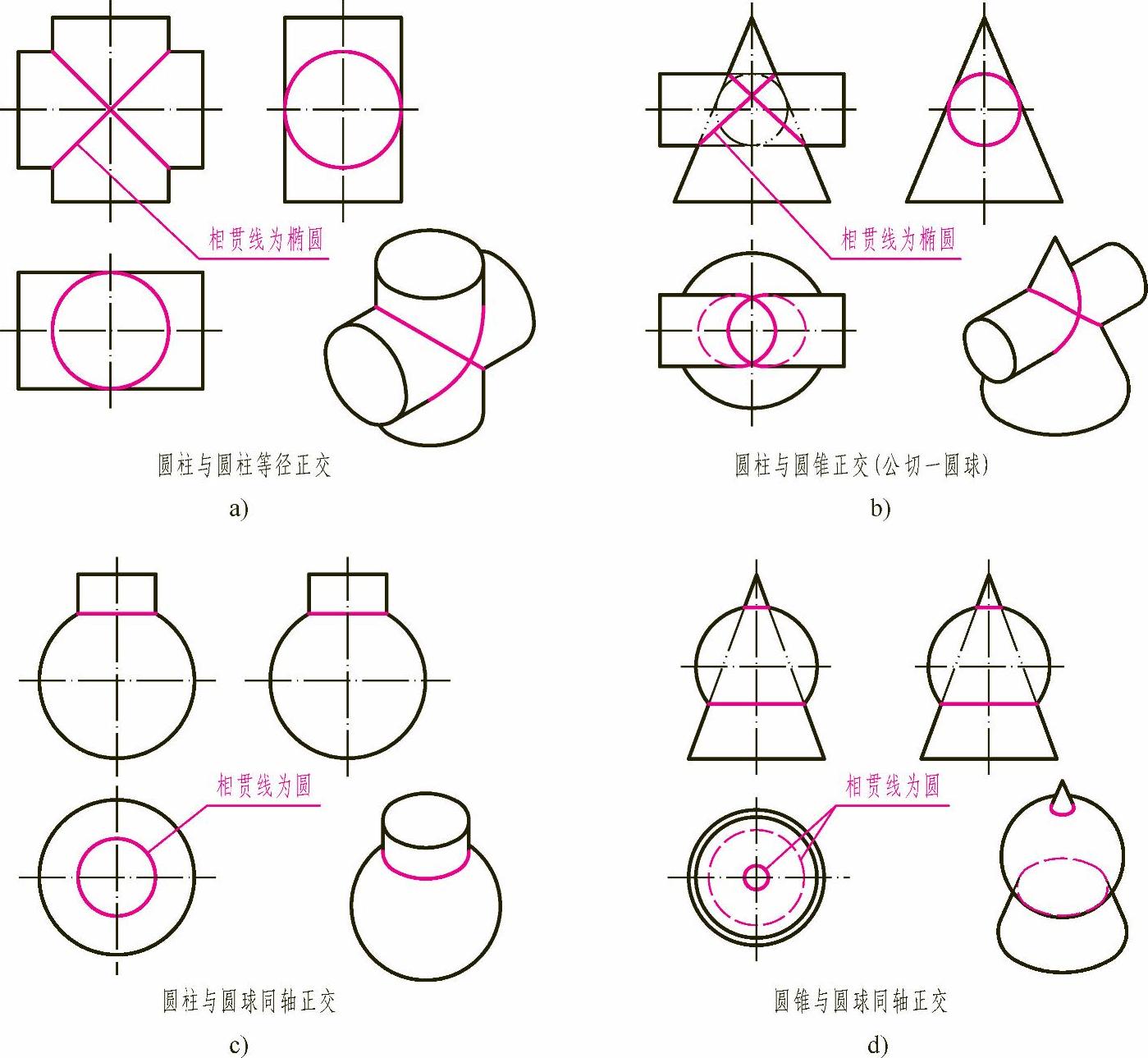
图3-11 同轴回转体的相贯线——圆

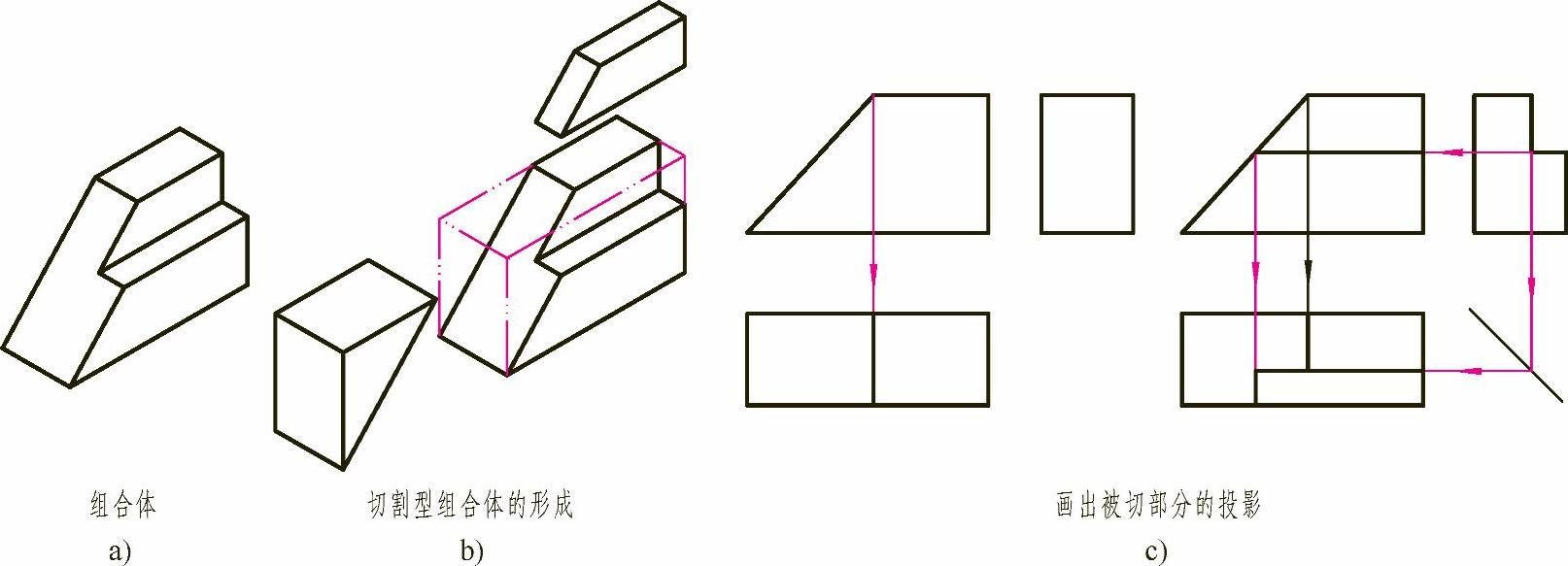
图3-12 切割型组合体的画法

5.综合型

大部分组合体都是既有叠加又有切割，属综合型。画图时，一般可先画叠加各形体的投影，再画被切各形体的投影。图3-13中的三视图，就是按底板、四棱柱叠加后，再切半圆柱、两个U形柱和一个小圆柱的顺序画出的。

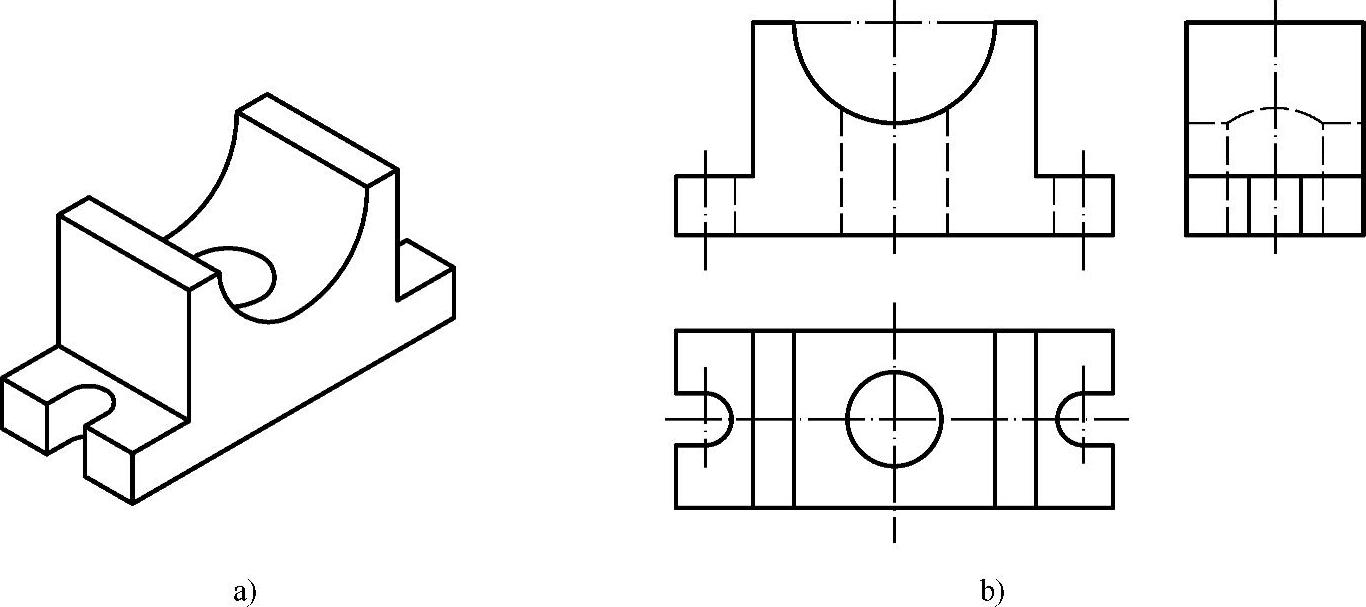
图3-13 综合型组合体