【摘要】:可采用有限元模型来计算线性弹簧和J弹簧的柔性程度。在有限元模型中,基板被建模为刚性体,并且采用被溅射金属的剩余应力梯度开始计算,能得到释放后弹簧几何结构。通过改变不同弹簧结构的几何参数,可进行柔性分析。图21.5所示为弹簧柔性随其长度的变化,而图21.6所示为J-弹簧的柔性随其圆弧段内径的变化。从图21.6可以看出,X柔性和Y柔性的曲线基本相互平行,即其增加的幅度基本一致。
可采用有限元模型来计算线性弹簧和J弹簧的柔性程度。在有限元模型中,基板被建模为刚性体,并且采用被溅射金属的剩余应力梯度开始计算,能得到释放后弹簧几何结构。接着,一个力载荷被施加在释放后弹簧几何结构的自由端,以便分析弹簧结构的柔性。而弹簧结构沿力载荷方向上的柔性可表示为,在力的作用点处,弹簧沿力方向上的位移大小和力载荷大小的比值。通过这种表示方法,可计算弹簧的柔性。通过改变不同弹簧结构的几何参数,可进行柔性分析。对于线性弹簧而言,可改变的几何参数是弹簧的长度和宽度。对于J-弹簧而言,可以改变的几何参数是长度、宽度、圆弧半径和包角。为了论述简洁,这里仅给出部分分析结果,更多的细节请见参考文献[25]。图21.5所示为弹簧柔性随其长度的变化,而图21.6所示为J-弹簧的柔性随其圆弧段内径的变化。
从图21.6可以看出,X柔性和Y柔性的曲线基本相互平行,即其增加的幅度基本一致。然而,由于长度也能对Y柔性产生影响,所以在此例中,Y柔性通常大于X柔性。最大的Y柔性大约比初始值大4倍,而最大的X柔性大约比初始值大8倍。这是因为Y柔性值同时受长度L和半径R的影响,而X柔性通常主要受半径R的影响。虽然Z柔性的大小和增长速率都大大高于平面柔性,但是与Y柔性类似,其最大值仍然大约只比初始值大4倍。半径R的增加,不仅会增加力矩臂,还会提高释放高度。由于这些效应,半径R对J-弹簧的柔性也有很大影响。
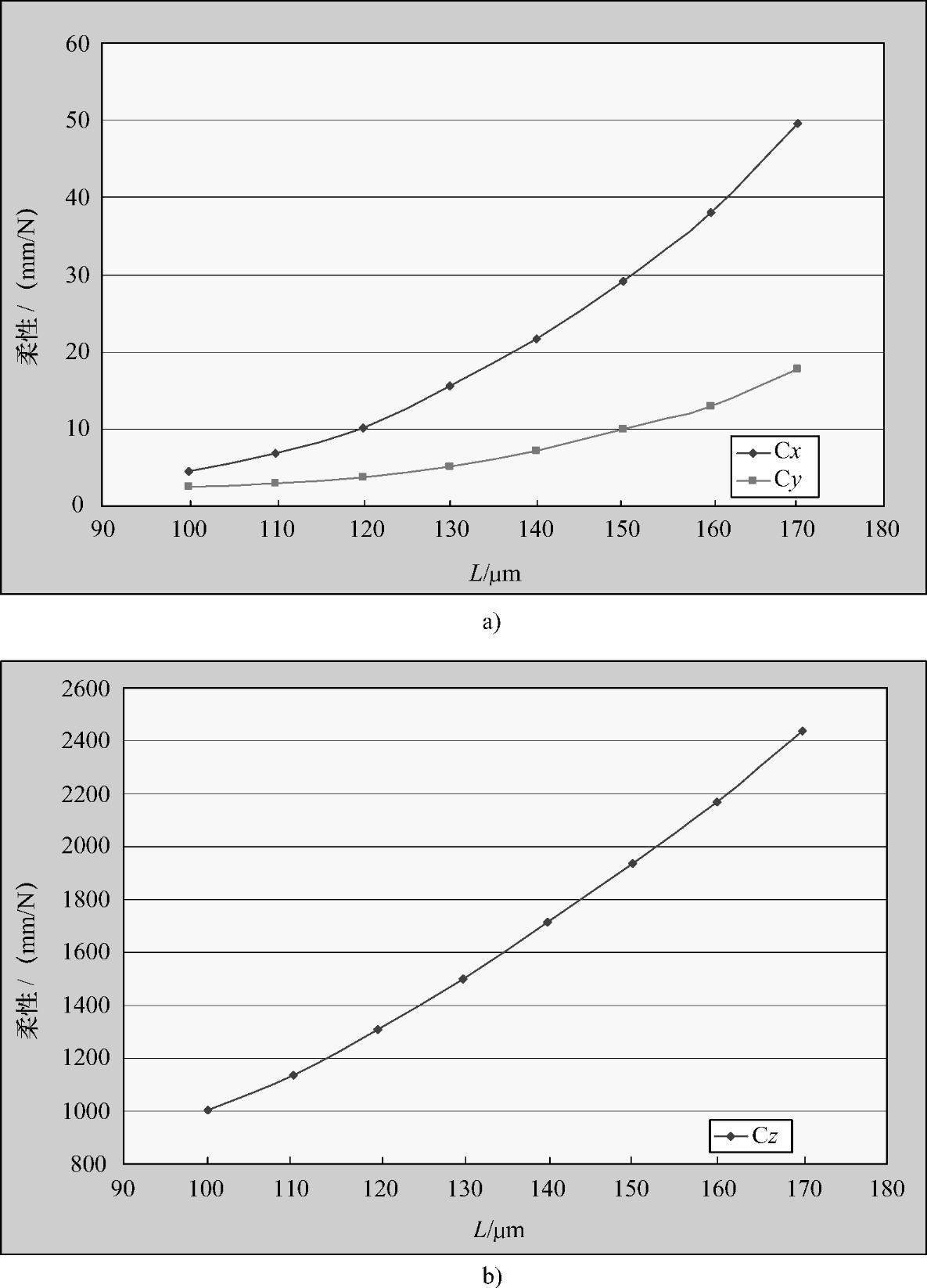
图21.5 板内和板外柔性随其长度的变化
a)板内 b)板外(https://www.xing528.com)
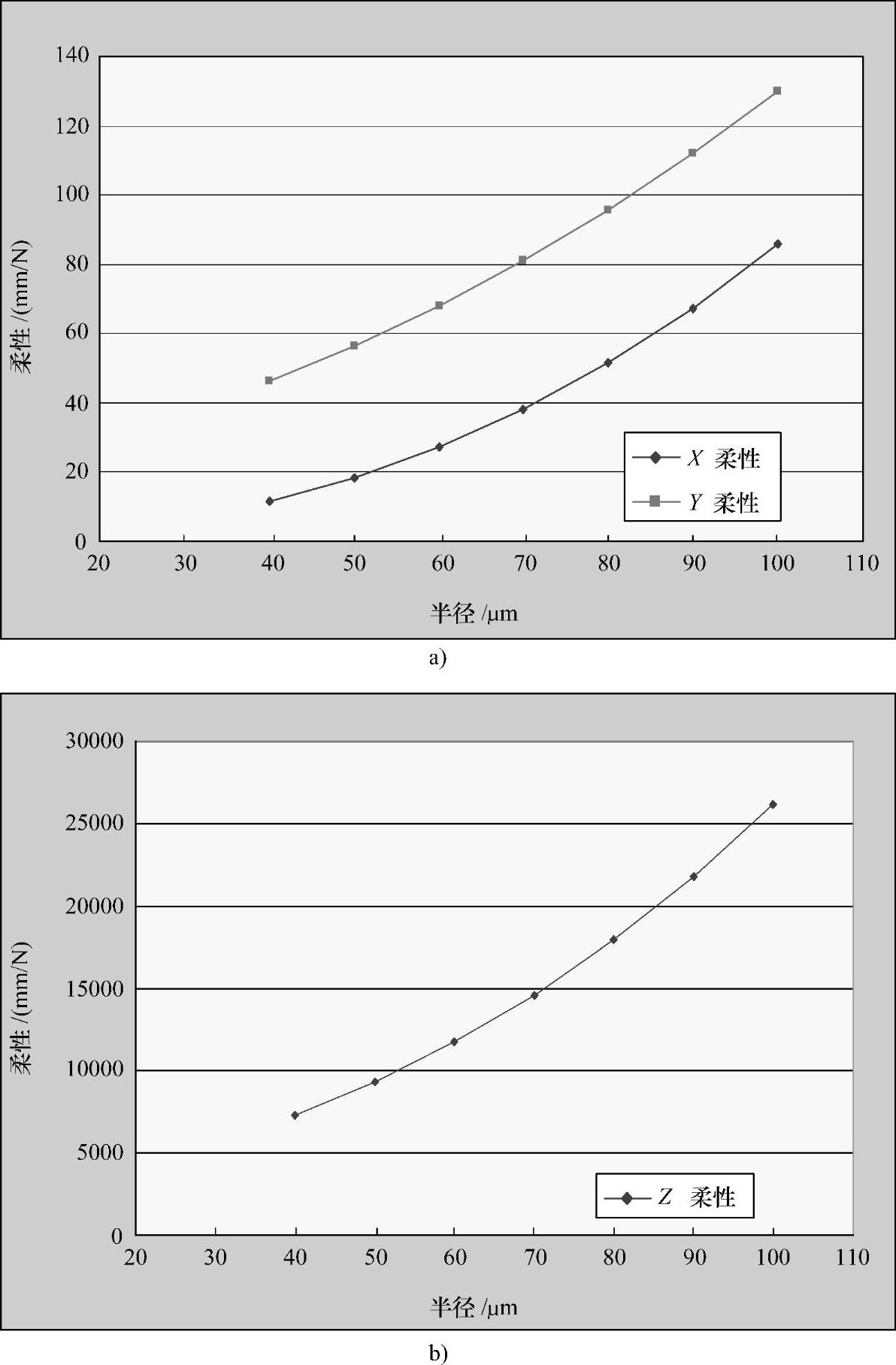
图21.6 J-弹簧板内和板外柔性随半径的变化
a)板内 b)板外
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




