如何提高材料的热导率？

在面积A上的传热量Q，取决于材料的导热系数（即热导率）k和温度梯度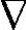T。热传导服从傅里叶定律，有

Q＝kTA （17.1）

若如果长度为l的一维结构上温差为ΔT，则

固体和液体中的热量传递通过晶格的振动（声子）和电子的迁移两种效应进行。因热传导涉及电子，故通常良好的导电体也是良好的导热体。绝缘体中无电子的转移，故绝缘体中的热传导必然依靠晶格的振动，因此更弱。

17.2.1.1 复合材料中的热传导

材料的密度越大、越均匀，热导率越高。不同类型的声子散射过程降低了绝缘体的热导率。复合材料的声子散射主要是由于填充物和基体^[2]间的声学搭配失调。当填充剂的种类和体积分数一定时，可采用如下方法来提高复合材料的热导率：

1）减少热阻接点的数目，例如通过使用较大的填充颗粒而最小化填充颗粒间聚合物层的数目等方法。

2）通过适当的包装以形成传导网络。(www.xing528.com)

3）使填充颗粒与基体结合面的缺陷最小化。

根据Lewis和Nielsen^[3]的半经验（semi-empirical）理论，可预测复合材料的热导率。根据这一理论，复合材料内的热传导取决于填充物的体积分数、填充物和基体的热传导及填充颗粒的形状。根据Lewis-Nielsen的理论，使用下式预测复合材料的热导率：

式中，ϕ_M为填充物的最大含量；A为取决于填充物颗粒形状的参数（对不同几何体；ϕ_M和A均以表格形式给出（实验值和理论值））；ϕ_F为填充物的体积分数；k_F、k_M和k_C分别为填充物、基体、复合材料的热导率。根据这个理论，在热导率和体积分数相同的情况下，杆和纤维比球体更能提高传热系数。然而该理论未明确考虑颗粒的大小和两相以上的复合材料等问题。Miloh和Benvebiste^[4]提出了一个方法，来估计含椭圆体填料的三相复合材料的有效热导率。

综上所述，显然，如果要产生高热导率的复合材料，复合材料中的填料颗粒必须是加长的且分散均匀的，并且须形成导热网络。通过对填充颗粒进行表面处理和在复合材料中添加偶联剂^[5-7]，可改善填充颗粒与基体界面处的接触情况。若不进行上述处理，环氧基体中的填充颗粒会形成集聚物。因此，需要对填料颗粒表面进行处理，使其表面呈现疏水性。偶联剂也可带有一个官能团以与聚合物基体形成化学键。

17.2.1.2 热阻

热阻R_th是表征系统冷却能力的一个常用方式。R_th与电阻类似，只是其驱动力为温度差而非电压，它定义为温度差除以热流量，即

电子系统的冷却可以通过热源（芯片）与其环境之间的热阻来刻画。热阻取决于热源周围材料的厚度、横截面积和热导率，以及这些材料对其周围流体（例如空气或液态冷却剂）的传热系数h。与作为材料固有性质的热导率相反，热阻取决于传热系统的几何形状，是传热系统的特有性质。