体积分数分别为10%和20%的底胶NUF2和NUF1松弛行为的预测结果与实验数据相吻合。模拟条件如下:固定边界条件施加在表面y=0的中间节点上;立方体表面y=0沿Y方向的位移量设置为0;以等节点位移形式在表面y=L上施加拉伸载荷;采用阶跃位移载荷而非斜坡载荷,以确保应变的瞬间施加;所施加的瞬间应变为1%,并在求解过程中保持定值。
纳米填充物颗粒当作线弹性来建模;而采用广义并联Maxwell模型的粘弹性特性来对环氧树脂基体进行建模;采用环氧树脂的Prony粘弹性剪切响应数据和Pro-ny粘弹性体积响应数据,来表征环氧树脂的粘弹性WLF常量数据。在应力松弛测试过程中,应变先从0开始斜坡加载到要施加的应变等级,之后再对试样进行应力松弛。在松弛过程中,试样的瞬时模量连续减少到一个显著低于初始弹性模量的值。在Prony常数计算中,最初的斜坡应力-应变被忽略,而假定瞬时应变和应力的加载时间为0。
通过测量拉伸试验中应力-应变曲线的初始斜率,可以知道环氧树脂的弹性模量值为2.5GPa。上述的弹性模量可能不适合粘弹性分析,因为施加的应变载荷是瞬时的。使用这个初始的弹性模量值可能会夸大底胶的松弛特性。因此,使用应力松弛开始时弹性模量的瞬态值来分析底胶的松弛特性。在这种情况下,分析所采用的弹性模量为1.84GPa。非线性求解通过采用若干个时间子步进行。计算出表面y=L的节点应力响应,并根据计算结果绘制,如图14.29所示。对体积分数分别为10%和20%的纳米底胶的松弛特性进行预测所得的结果和实验测量获得的松弛特性能吻合良好。(https://www.xing528.com)
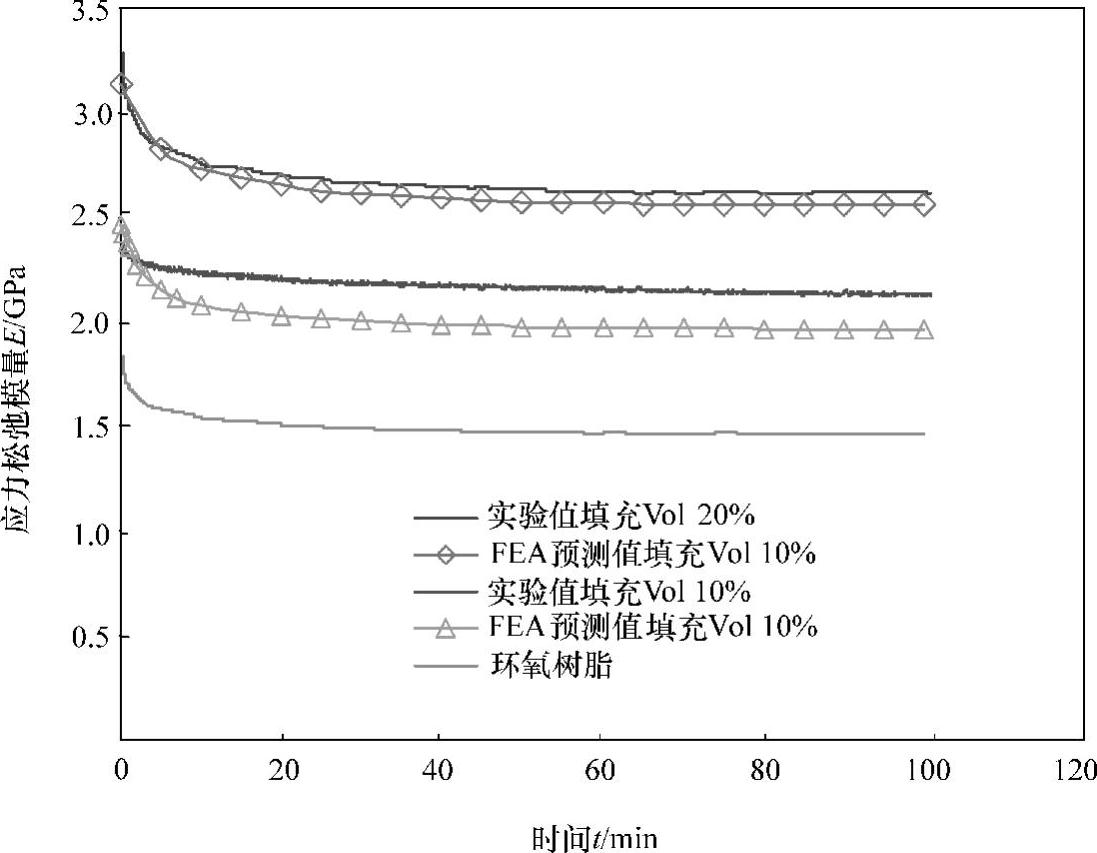
图14.29 纳米底胶NUF1和NUF2的弹性模量松弛量的预测值
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




