本研究中,ANSYS有限元分析软件被用来计算上文所建立的单元格模型的时间依赖性行为,并采用WLF(Williams-Landel-Ferry)平移函数常数和体积剪切响应的普朗尼级数常数对纳米底胶建立模型,WLF平移函数是利用弹性模量松弛数据和时间-温度叠加法计算得到的。
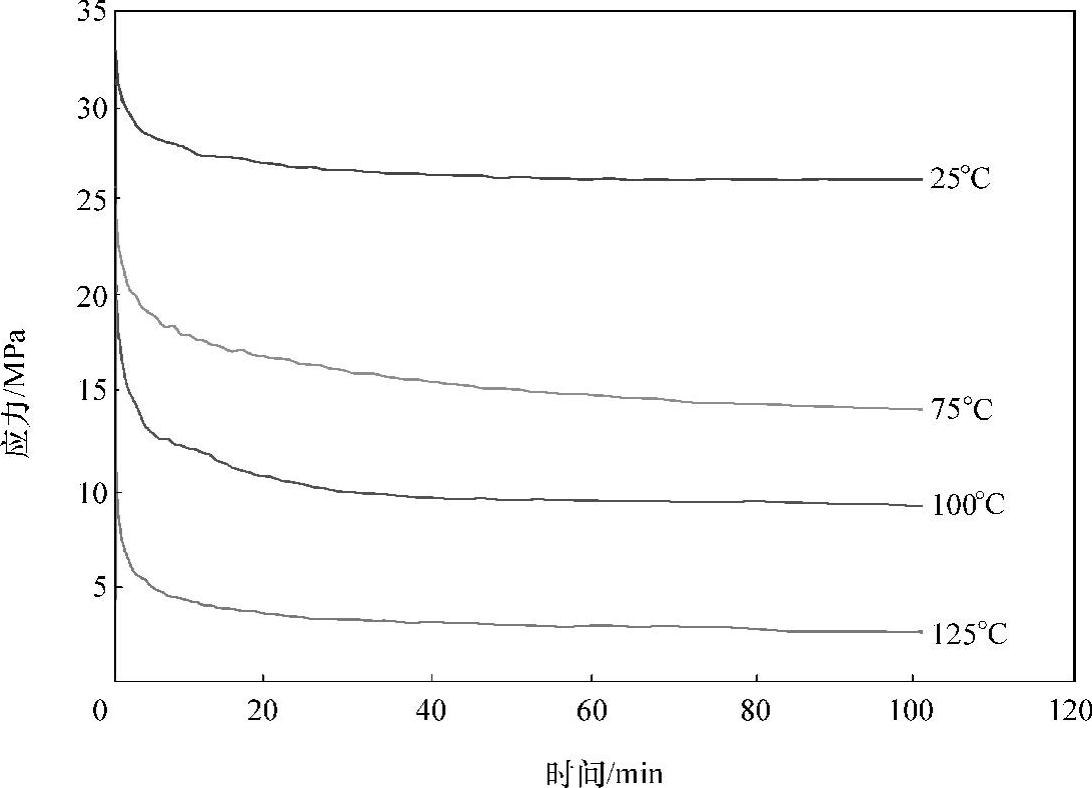
图14.14 用于计算粘弹性常数的应力松弛数据(1%应变)
图14.14所示为用于计算粘弹性常数的应力松弛数据。图14.15所示为对数-对数图,其纵轴为从图14.14所示曲线获得的温度依赖性松弛模量的对数,其横轴为加载时间的对数。把图14.15所示的25℃时应力松弛曲线当作参考曲线,把75℃、100℃和125℃下的相应曲线沿时间轴横向平移适当的距离,则会形成图14.16所示的单向主应力松弛曲线。每条曲线相对于温度的偏移系数如图14.17所示。WLF常数可通过将温度依赖平移系数aT和温度值代入式(14.11),然后对该方程进行线性回归得到。本研究中,纳米底胶的WLF常数为C1=T0=25℃,C2=-42.6,C4=517℃。下式最初由Williams、Landel和Ferry提出,它给出了平移系数和温度之间的关系:

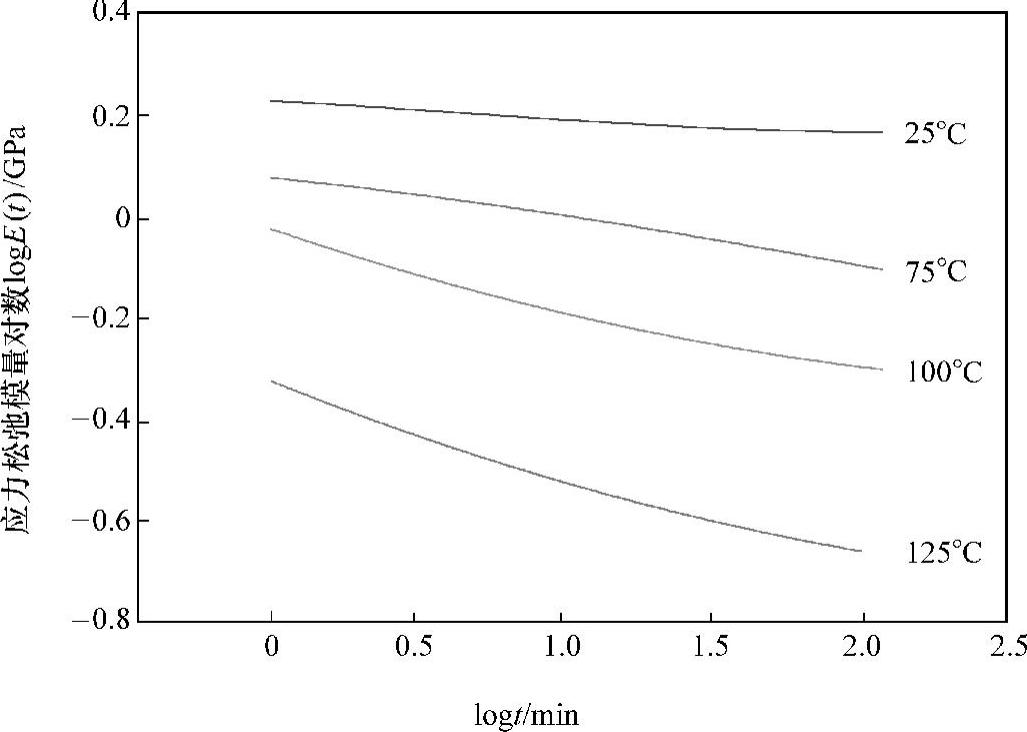
图14.15 松弛模量-时间的对数-对数图
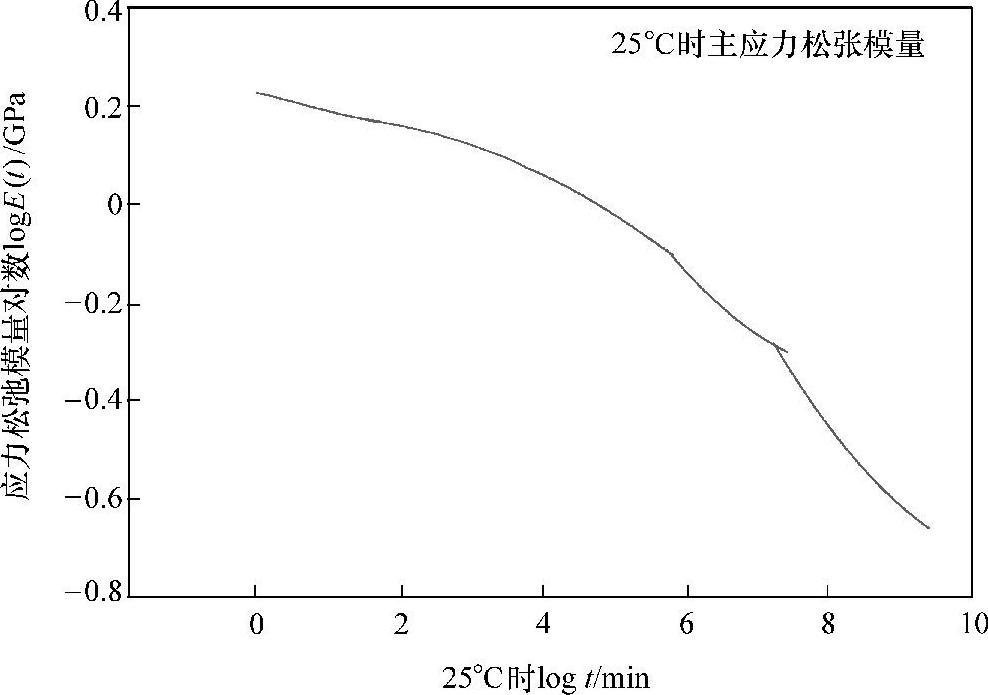
图14.16 25℃时主应力松弛模量
描述体积响应和剪切响应的粘弹性常数使用普朗尼级数来计算,普朗尼级数由广义的并联Maxwell模型求解得到。弹簧和阻尼器的应力-应变关系可以描述为
σ=kε2 (14.12)

总应变为
ε=ε1+ε2 (14.14)应变速率为

将式(14.12)的时间导数和式(14.13)代入式(14.15)中得到

或者表述为

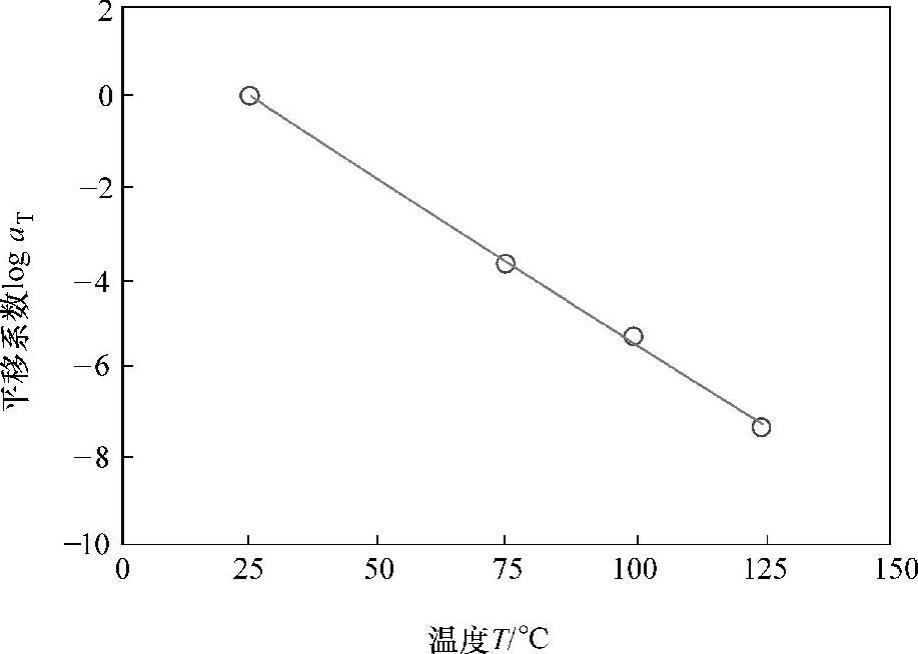
图14.17 依赖温度的平移系数
对式(14.17)进行拉普拉斯变换,有
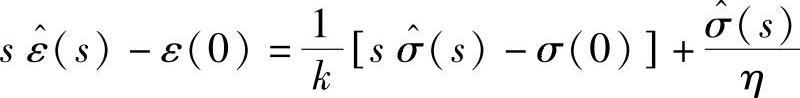
由于ε(0)=σ(0)=0,上式简化为
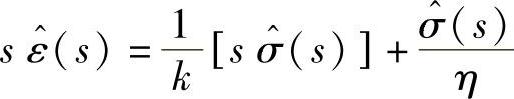
整理上式得到

假定施加的应变为一个阶跃函数ε(t)=ε0H(t),则有(https://www.xing528.com)
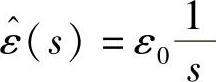
将它代入式(14.18)中得到
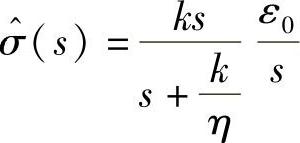
或者写为

对式(14.19)进行拉普拉斯反变换得
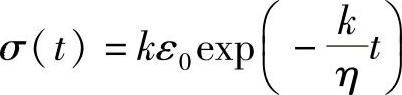
设τ=η/k,得

如图14.18所示,广义Maxwell模型由若干元件并联而成。由于Maxwell元件相互并联,应力松弛响应为每个元件的应力松弛响应之和。对于该模型有

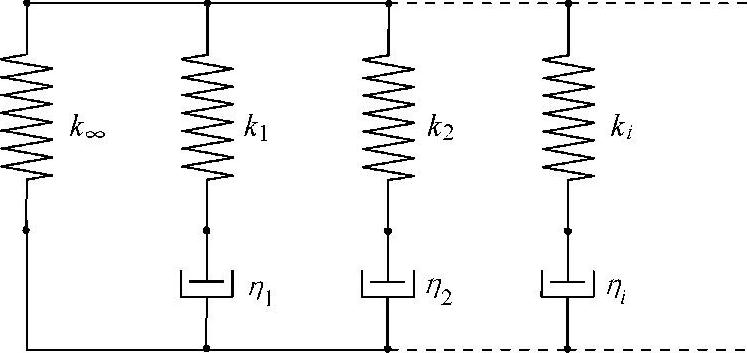
图14.18 带有并联自由弹簧的广义Maxwell模型
代表弹性模量的普朗尼级数可通过把应力响应方程除以恒定应变ε0得到。应力响应方程除以恒定应变ε0得到的普朗尼级数形式如下:

并联有一个自由弹簧模量k∞的广义并联Maxwell模型(见图14.18)对恒定应变ε0的模量松弛响应如下:
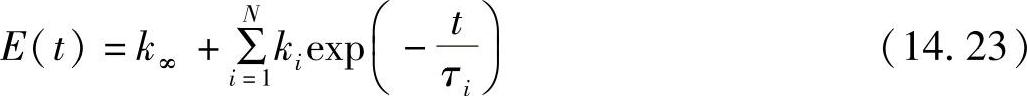
用E代替k得
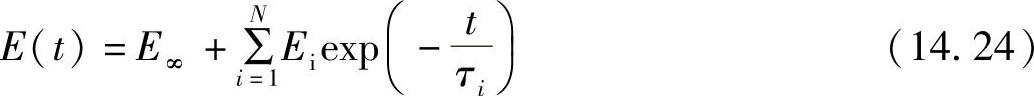
ANSYS软件允许采用至多十个Maxwell元件来近似计算松弛函数。式(14.25)和式(14.26)用于近似计算剪切模量和体积模量的松弛量。
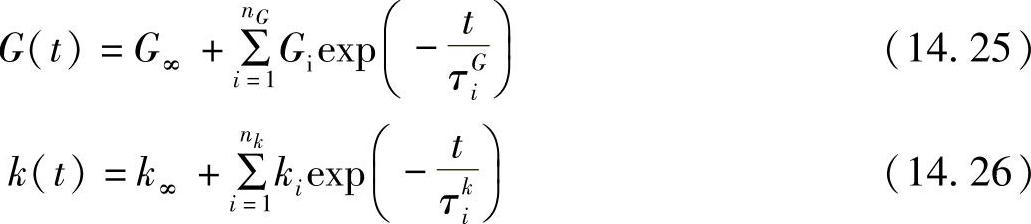
式中,G∞为最终剪切模量(GPa);k∞为最终的体积模量(GPa);nG为Maxwell元件的个数,Maxwell元件用于近似计算剪切模量的松弛量;nk为Maxwell元件的个数,Maxwell元件用于近似计算体积模量的松弛量;τiG和τki为每个Prony部件的松弛时间。
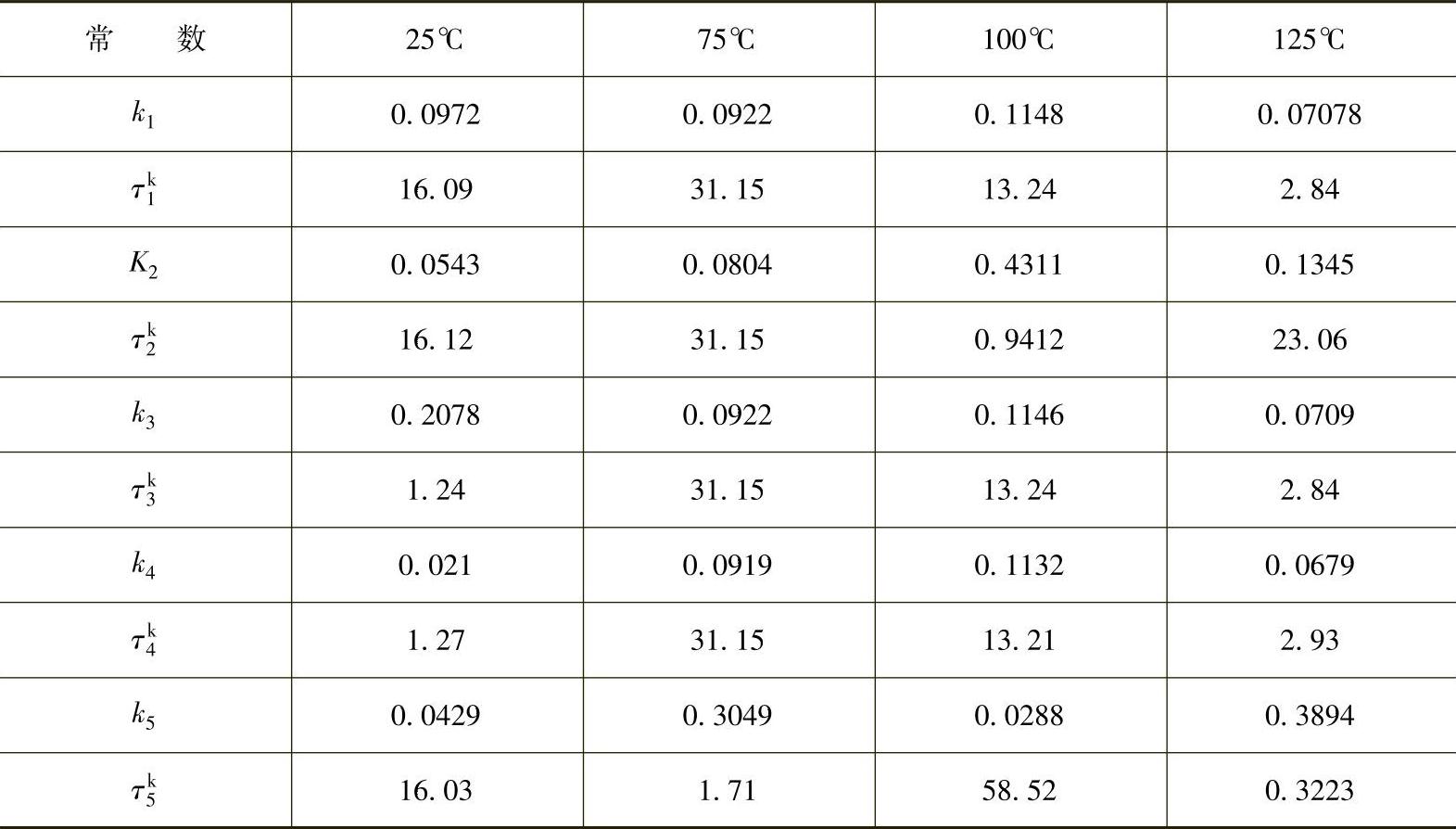
本研究总共考虑了5个Maxwell元件。时间相关Prony常数通过对式(14.24)和式(14.25)进行非线性回归计算得到。表14.3和表14.4给出了计算所得的Prony常数系列。
表14.3 Prony粘弹性剪切响应
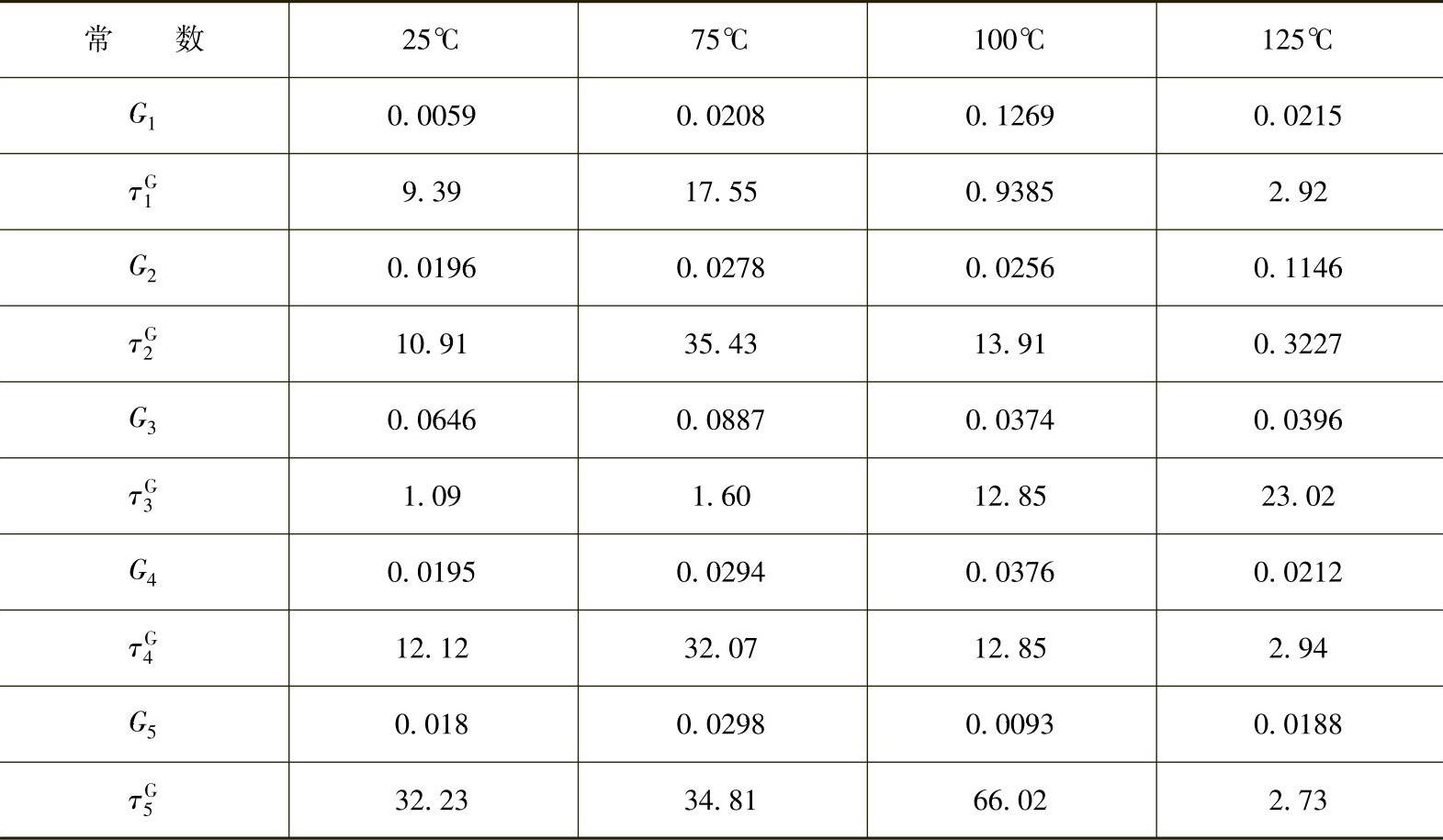
表14.4 Prony粘弹性体积响应
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




