建立立方单元格的方法与注意事项

纳米底胶的弹性模量和热膨胀系数可通过立方单元格的隐式有限单元模型来预测。底胶的立方单元格（简称为“立方体”）是通过球形填充颗粒在环氧树脂基体中的随机分布而产生。立方单元格的体积是L³，N是单元格中颗粒的总数，r是球状填充颗粒的半径。立方单元格中填充颗粒的体积分数γ取决于填充颗粒体积占立方单元格体积的比例，有

在满足立方体单元边长L的要求下，改变球粒的数目N能控制立方单元格中填充颗粒的体积分数。在所有体积分数的分析中，球形颗粒的半径r保持为定值。填充颗粒的分布状态应能保证立方单元格的各向同性，即立方单元格的特性在各方向上相同，并且能保证立方单元格适宜于采用有限元网格建模。基于改进型随机连续吸附算法（RSA）的算法用于产生底胶中纳米二氧化硅颗粒的随机中心坐标^[17]。在这个算法中，颗粒的所有可接受随机坐标（γ＝0～0.25）均满足以下条件：

（1）如果颗粒表面和立方单元格表面接触或者非常接近，这可能导致无法划分有限元网格或者所建立的有限单元网格是扭曲的，甚至根本不能划分网格。为了避免上述情况的发生，立方体中的颗粒必须同立方体表面保持一个最小距离d₂。

d₂＝r＋0.1r（14.2）

为了满足以上条件，第i个颗粒的中心坐标必须通过以下检查。

x_jⁱ≥d₂；j＝1，2，3

x_jⁱ-L≥d₂j＝1，2，3 （14.3）(www.xing528.com)

（2）如果相邻的两个颗粒相互重叠，则这违背刚性球体的条件。此外相邻的两颗粒也不能相互接触。为了满足这个条件，第i个颗粒的中心坐标必须通过以下检查：

改进型RSA法所能实现的体积分数高于γ＝0.25。当立方体单元格的体积分数位于0～0.25时，所有的填充颗粒都在单元格内部，且无颗粒同立方体的外表面重叠。对于体积分数大于0.25的立方体单元格，填充颗粒被允许与立方体的边界面重叠。如果有任何颗粒同立方体表面重叠，在立方体外面的颗粒部分被细心地划分为几个部分，并将划分好的部分复制到该表面相对面的合适位置处（颗粒物依然在晶胞的内部）。首先，通过上述的两个条件产生填充颗粒体积分数小于0.25的立方体单元格，然后在保持球体颗粒尺寸不变的情况下压缩单元格的尺寸。在晶胞尺寸压缩的整个过程中，球体颗粒的尺寸和数目保持不变，但是因为晶胞的尺寸减小了，所以填充颗粒的体积分数会更高。首先，采用一个用户自定义的收缩因子C_f（<1）与立方体的边长L相乘来压缩立方体的边长。压缩后的立方体边长表示为

L_n＝c_fL （14.6）

第i个颗粒压缩前的中心坐标为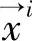，压缩后这个颗粒物的新位置为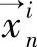，即

颗粒移动后，允许它们同立方体表面重叠，但是颗粒的中心不允许在立方体以外。如果第i颗粒的新坐标^→xⁱ_n落到立方体的外面，则它将被移回到立方体内，并被放置在立方体表面和另一个平面之间的任意位置，这个平面与立方体表面相距（r-a）。其中，α为用户自定的常数，且α>0.1r。如果颗粒物的中心与立方体表面的距离为r，则颗粒物表面会与立方体表面接触，这使得网格划分无法进行。如果第i个颗粒的新坐标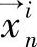位于立方体内部，且处于立方体表面和与表面间距为r的平面之间，则它将被移到立方体表面和与表面向内距离为（r-a）处之间的任意位置。其中，α为用户自定义的常数，并且α>0.1r。如果颗粒的新位置同之前可接受的位置重叠，则它将以任意方向移动至一任意新位置。新的位置表示为

式中，β为一小随机数。β越小能确保越快的收敛。仅当满足以上提到的所有条件时，颗粒物的新位置才会被接受。由于RSA算法涉及随机移动和随机定位，每一次迭代未必能产生可接受的颗粒分布。这个算法会计算迭代的次数，如果迭代的次数超过了一定的数目，程序的运行会终止。