纳米结构电阻材料的概述

纳米结构电阻材料是由导体和绝缘体组成的复合材料，有两种类型：第一类包括金属和绝缘体经物理或化学混合而制成的薄膜，通常可归于金属陶瓷范畴。金属陶瓷薄膜可由不同方法制备，例如蒸发法、在富氧条件下溅射易氧化金属^[5，6]、共蒸发法^[7]、共溅射法^[8]、等离子聚合和金属蒸发同时或交替进行^[9]及在金属离子中注入聚合物^[10]等方法。另一类是非连续金属薄膜，它形成于蒸发法^[11]或溅射法^[12，13]中沉淀金属薄膜的初始阶段。

二维不连续金属薄膜有三个生长阶段。在生长的初始阶段，离散的核形成，一旦核包含数个原子，它们一般会比较稳定。离散的核通过捕获表面迁移原子或者直接从气相中捕获原子等方式长大，而成为离散的颗粒。当颗粒间距离降到几纳米时，直流电流可穿过薄膜。随着颗粒的进一步增长，薄膜的生长进入合并阶段。这个阶段通常伴随着电阻的大幅度降低。最终，颗粒合并完成，这导致金属毛细管互连网络的形成，且该金属网络的导电性能接近正常金属。这类结构的重要特征是，薄膜的整体电阻由毛细管的连接方式决定，而不是由毛细管的电阻率决定。每单位面积上由相同金属组成的薄膜的电阻却差别很大，这是因为金属在基体内的分布不同。第三个阶段的结构是连续金属薄膜，它形成于毛细管之间的空隙被填补并且薄膜接近平面平行板时，一般为多晶体金属。在这个阶段，表面和晶界散射决定了薄膜电阻系数的大小。图8.1所示为铝薄膜三阶段结构的原子力显微镜（Atomic Force Microscopy，AFM）图^[13]。

图8.2所示为不连续铝薄膜片电阻随沉积时间变化图^[13]。

在连续金属薄膜中，电子传导保留了大块金属材料的大部分特征。例如，当0.7<x<1^[14]（x为镍在复合材料中占的原子百分数）时，镍-二氧化硅粒状薄膜显示出了大块材料的铁磁性。然而，对薄膜而言，基于电子平均自由程的特性却发生了巨大改变，这是由于电介质颗粒和晶界处存在强烈的电子散射。例如，与晶体的电导率相比，薄膜的电导率呈现大幅递减，薄膜的电阻温度系数（Temperature Coefficient of Tesistance，TCR）虽为正值，却远小于大块金属材料的相应值^[15]。

对由纳米大小的孤立金属颗粒所组成的薄膜而言，有两个重要的物理参数，一个是基体辅助的电子传导^[16]，另一个是两中性金属颗粒之间转移一个电子所需要的热激活充电能^[11]。

在金属毛细管随机互连网络薄膜这一过渡结构中，电子的传导特别引人注意，因为它涉及渗流理论的数学问题。这种结构中的电子传导是由沿金属毛细管的渗流和孤立颗粒间电子隧道效应形成的。如前所述，孤立颗粒间的电子传导会使薄膜的电阻温度系数变为负值，而电子在毛细管网络内的传导类似电子在正常金属中的传导，尽管电阻温度系数降低了，但仍为正值。

纳米结构电阻材料中，非金属传导向金属传导的转变是由基体所含金属的体积或面积分数决定的。把基体视作正交晶格，而金属核只能在晶格的节点生长。随着生长的进行，相邻核互相接触和凝聚。尽管在高温极限下，两个原子核聚合可能形成近似球形的核，但通常聚合会形成拉长的毛细管状物。因此，金属核构成节点，金属核的大小决定金属核之间相互作用的强度，而毛细管则相当于键。这一渗流理论有两个基本问题：一个是节点问题，即薄膜的物理性质会随晶格上被占据节点的比例而变化；另一个是键问题，即当前存在的键会发生变化。依电子传导的观点，需要确定薄膜从金属向绝缘体转变的发生阶段。事实上，粒状金属薄膜没有突然的转变阶段。这是因为薄膜中有一系列的结构，在这些结构中颗粒间电子传导和金属毛细管内的电子传导会同时进行，并且初始阶段两者对电阻的贡献几乎相同；而最终，毛细管将完全取代隧道效应，成为电子传输的途径。Scher（谢尔）和Zallen（扎伦）^[17]得出，在大规模的互连路径形成后，二维晶格上被金属覆盖的面积占晶格总表面积的44%。

对薄膜的结构和电气传输数据进行分析，可得出粒状金属薄膜参数的详细信息：金属平均粒径，金属颗粒平均间距，以及金属颗粒的分布情况。

图8.1 铝薄膜三阶段结构的原子力显微镜图^[13]

a）核化阶段 b）合并阶段 c）连续膜阶段

电子在两个初期中性岛状金属颗粒间传递，必须做功来克服库仑力。因此，对于半径为r的金属颗粒而言，其上惟一能传递的电子必须被激发至一个能级状态。这个状态的能级的数量级与e²/4πεr相同，且高于该金属颗粒的费米能级^[18]。其中，e是电子电荷，ε是介质的有效介电常数。

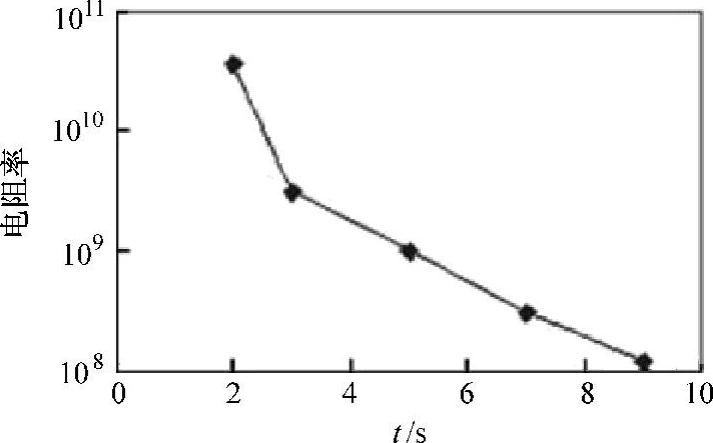
图8.2 电阻率随沉积时间的变化^[13]

激发电子所需的能量可由温度T的热能提供，若服从玻耳兹曼统计，带电颗粒的总数n由下式得出：(www.xing528.com)

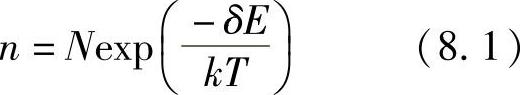
式中，N为薄膜中颗粒的总数；δE为克服库仑力所需的活化能，可由Neugebau-er和Webb公式得出，即

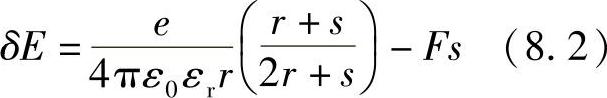
式中，s为颗粒间距；F为外加电场力。

激活隧道传导模型中，薄膜的电导率为

式中，K为几何常数；D为颗间隧穿概率。

在过去几十年里，Neugebauer和Webb理论和其他延伸模型^[19-22]已能很好地解释一些实验现象，并且和实验定性地符合。实验活化能和理论活化能δE的一致，充分确证了静电激活隧道效应的基本原理。而静电激活隧道效应是库仑阻塞效应的基础。然而，在粒状金属薄膜中电子的运输机理被完全解决之前，仍存在很多问题：

1）绝对电导的实验值比理论值大几个数量级。

2）尽管采用了可变程跳跃概念和渗流理论，分布式r和s的统计效应及岛（颗粒）的形态仍未能成功地包含在这些模型内。

3）尚不清楚，在活化能中是应采用高频介电常数还是应采用低频介电常数。

4）下面段落中的实验结果与现存理论不符，这就需要对基本的热激活隧穿机制做重大修改。

Borziak等人^[23]报告了三个重要实验。在第一个实验中，在电极上沉积金属颗粒后，他们采用快要相连的不同岛状颗粒结构制备了不连续金属薄膜，且薄膜有更小的岛状颗粒和/或更大的间隙。对这些对称的“非均匀”薄膜而言，在薄膜的阳极有更大的压降。在第二个实验中，在这种薄膜中观察到了稳定、可重现的开关现象，但这种现象的解释尚不明确。第三个实验中，他们通过在两极使用不同的非均匀结构，将非均匀薄膜制成非对称的薄膜，而所得到薄膜的直流电阻具有类似于二极管效应的极性依赖现象^[24，25]。

Morris^[25]已经开始研究交流下非对称薄膜的特性。传统模型认为，薄膜是相同岛状颗粒/间隙元素组成的阵列，且间隙隧道电阻R_g和电容C_g并联后，与金属岛电阻串联，其中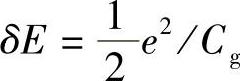。在交流下测得的电容C_g，通常比符合活化能的电容值大几个数量级。非对称非均匀薄膜有两个角频率，这使R_g和C_g各有两个不同值，两个值分别对应于两个电极。另外，C_g与在一个间隙距离下电极和薄膜的电容值匹配得很好。在极端不对称情况下，当一个接触电阻值变得非常大时，会产生“伪感应”现象，并通过把载流子注入薄膜使薄膜建立稳态电导的时间延迟。这种载流子能提高电导率，使之大于玻耳兹曼分布对带电岛电导率的预测值^[26，27]。预计这种二维效应在三维陶瓷电阻薄膜中同样适用。