半径为r的球状导电颗粒的电势能为
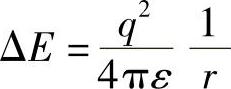
式中，q为颗粒所带的电荷；ε为该颗粒周围介质的有效介电常数；ΔE为将电荷-q从中性球体处移到无穷远处电场力所做的功。如果只需将该电荷从中性球体处移动到与之相距s的一个触点或颗粒量子岛，则电场力做的功减少（见图5.4）至[4，53]
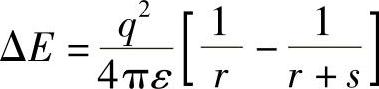
在N∞个纳米颗粒的集合中，Maxwell-Boltzmann（MB）统计学预测表明，有n个颗粒将被充电，有[4，53]
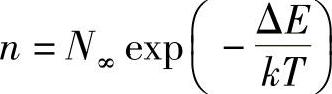
类似地，单个纳米颗粒按exp（-ΔE/kT）比例随机地进行热充电[54，55]。
应用电场F会使热充电能减小[56]，因为电场能提供纳米颗粒热充电所需的部分能量（见图5.5）[54]。当场强足够高时，纳米颗粒间的静电势垒会完全消失，这是纳米颗粒间经“库仑阻塞”而导电的典型条件。在“库仑阻塞”的起始点和漏端子之间，含有一个导电纳米颗粒量子岛；其他离析物足够小，足以发生电子隧穿。在温度为0K时，阈值电压V＝ΔE/q；但是在有限温度下，由于热荷的影响，I-V曲线在非线性阶段是圆形的，直到T趋近ΔE/k时非线性特征消失。这些影响在图8.15和图8.16所示的曲线上可能会出现。
实际上，正如上面提到那样，绝缘衬底上的小金属量子岛呈现偏心率为e的扁椭球形，因而热荷能必须被修正（记R＝2r＋s，p＝s/R）为[57]
当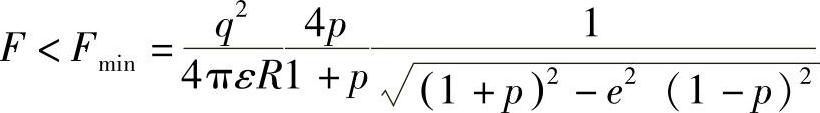
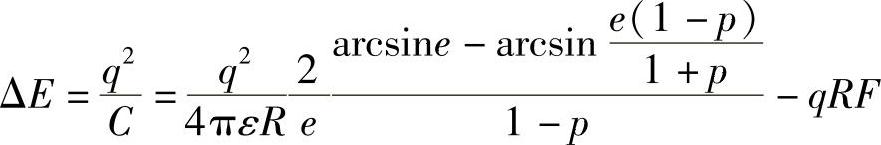
当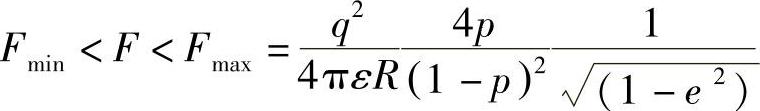
(www.xing528.com)
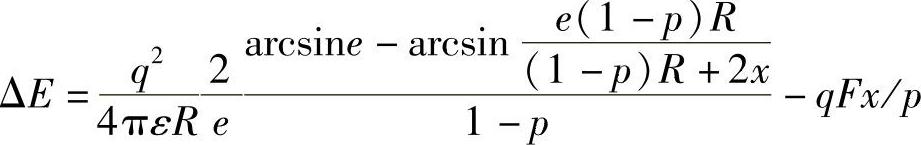
式中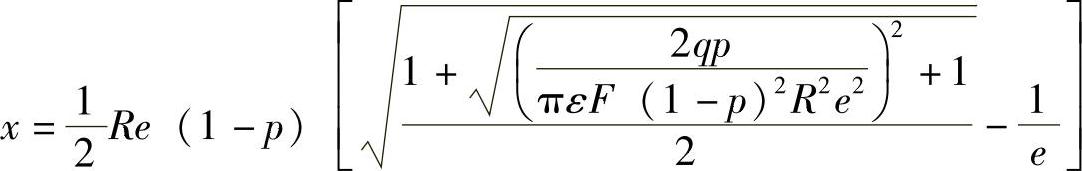
当F>Fmax ΔE＝0
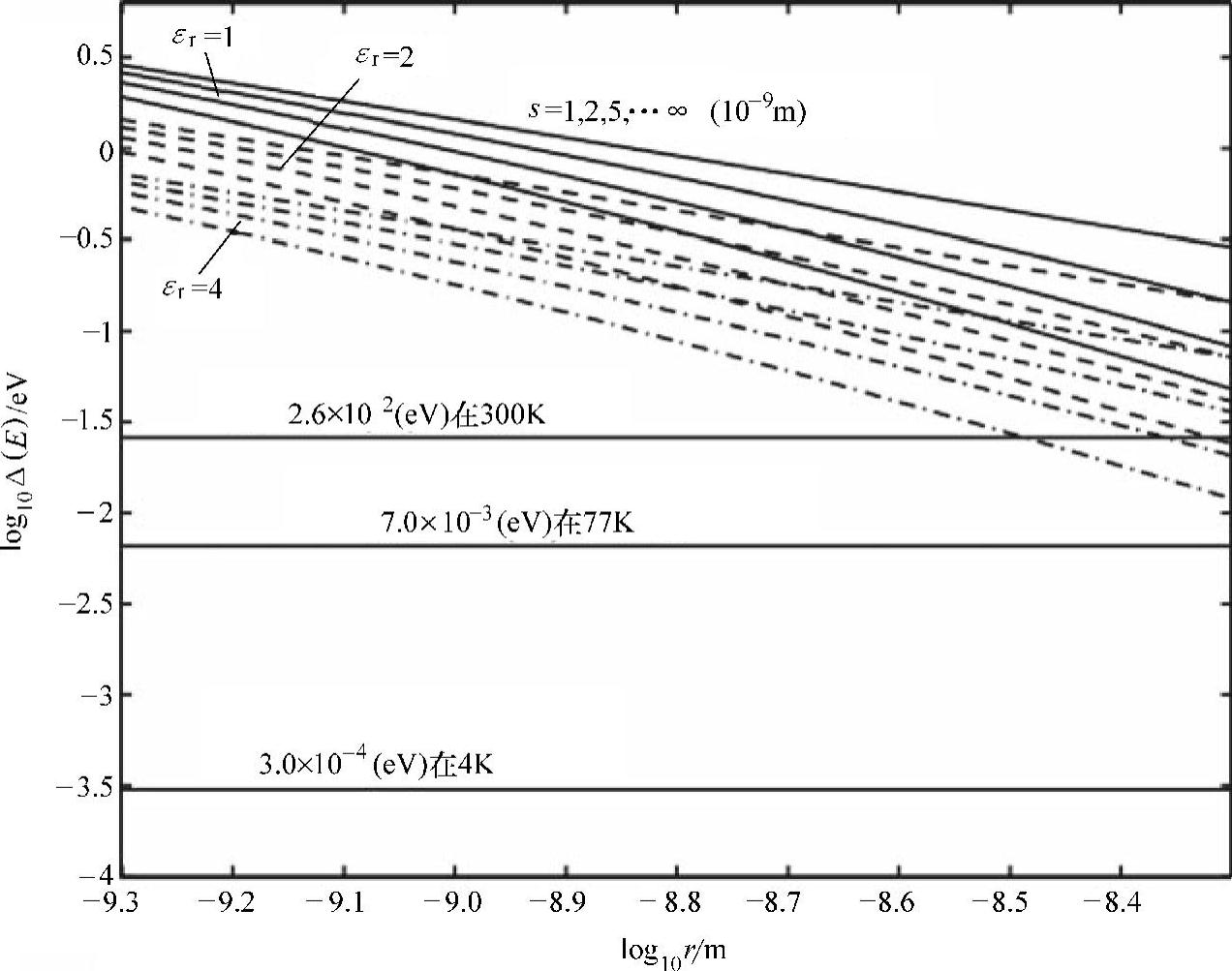
图5.4 静电电荷充电能ΔE是量子岛半径r的函数[54]（三组线分别对应εr＝1（最上端），εr＝2，εr＝4。每组线中，四条线的分类间距分别对应s＝1nm（最底端），2nm，5nm，∞。 热能kT分别对应T＝4K、T＝77K和T＝300K）
纳米组件通过电子隧穿进行热、电传导[4]，因而热导率满足下式：
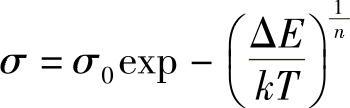
式中，1≤n≤3[4]。按MB分布的带电量子岛被注入的电荷覆盖，并在薄膜内产生了一个空间电荷分布和一个非线性的电场分布[58-60]。薄膜内的阻力对环境中的气体敏感，因为这些气体能够调节金属的功函数，从而调节隧穿势垒的强弱[61，62]。钯/氢气的结合是独特的，因为钯晶格中溶解的氢气会同时改变贯穿隧道的宽度和高度[63-65]。外加应力的作用也会改变隧道的间隙宽度，使得灵敏系数很大。在外加应力也影响到ΔE之前，灵敏系数与s为线性关系[66]。DMTF基底[67]（或绝热金属陶瓷基底[3]）的极化或内部的离子漂流，会导致其特征和残余电流出现长期漂移或滞后效应。量子岛通过表面自扩散会向其热平衡形状逐步演变，这也导致其电气特性的长期漂移[68]。同样的，当材料的温度系数为负值时，量子岛薄膜和金属陶瓷会受到热击穿作用，这种作用会导致热量的转换[69]。在这些薄膜中，也已经观察到可再生的转换[3]。
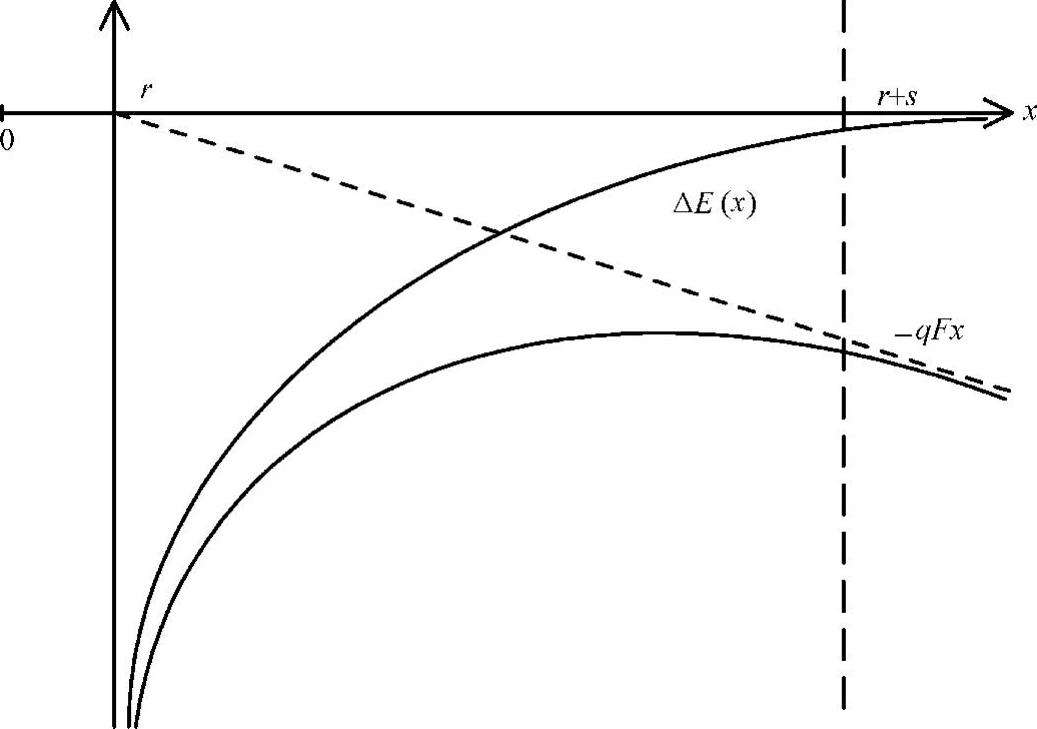
图5.5 半径为r时，颗粒量子岛的静电电荷充电能[54]
（当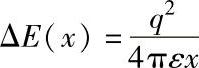
时，复合函数ΔE（x）-qFx在高场强下取最大值）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
