纳米颗粒尺寸对熔点降低的影响及统一解释

当颗粒尺寸变小时，颗粒的表面能会增加^[28]，因此纳米颗粒材料的熔点（Melting Point，MP）可能远低于其对应大块材料的熔点^[28-32]。同时，相对于大块材料，纳米颗粒的表面曲率大大增加^[33]，这导致颗粒的蒸气压增加，进而导致纳米颗粒融化时会快速蒸发。人们研究这些现象已经数十年了。如图5.2^[29]所示，对于三种不同的金属，熔点曲线的变化说明，可能存在一个统一的理论来解释各种纳米颗粒的熔点下降现象，而且仅当纳米颗粒的尺寸在5nm或更小时其熔点下降才较为明显。

图5.2 金、锡、铅的实验熔点，归一化为对应大块物体的熔点^[29]（授权使用）

各种不同的电子显微镜检查技术已经被用来测定纳米颗粒的熔点。例如，Sambles^[29]在温度受控的条件下监测了小颗粒的蒸发过程，并记录了蒸发率改变时的颗粒尺寸，他认为这个温度就是该尺寸下颗粒的熔点。其他研究人员注意到电子衍射环从轮廓鲜明向漫射转变^[34]或者突然消失^[35]。Allen等人^[34]利用暗场像，来说明图像消失时的对应温度为熔点。或许有人认为晶体平面消失对应着晶体的熔化，但这在小尺度下不适用，因为固体颗粒可能不存在离散化的小平面^[34]。对比暗场图和明场图，发现熔化过程分为两步：围绕晶核的表面液层温度达到固相点时，熔化开始；随着温度的上升，固体的结晶内核逐渐减小，当温度达到液相点时，熔化结束^[36]。

在融化过程的第一步中，对于半径为r的颗粒，其熔点T_M与其对应大块物体的温度T∞可能满足如下经验关系式^[34，37]：

(www.xing528.com)

式中，r₀为颗粒在0K温度下保持液态的极限半径^[38]。相比较而言，两个最接近上述理论的是热力学模型^{[34，35，39-41]}和“表面层”模型^[37，42]。一般地，不同热力学模型中，r₀值不同（尽管也有人^[40]建议使用公式T/T∞＝1-（r₀/r）²）。已经证明纳米颗粒表面存在一个类似液态的外壳^[42]，而且通过按下面的方程式调节外壳层的厚度t₀，可以使理论计算与实验吻合良好^[42]：

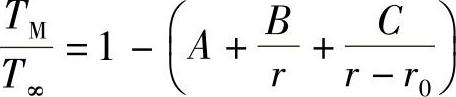
式中，A、B、C均为热力学常数。合金系中存在组分的相变，导致两步熔化过程更加复杂^[36]。

因为无铅焊料的熔点很高，所以与常规锡-铅共晶焊料相比，它的热机械应力更高，并且降低无铅焊料的熔点可能是降低其工艺温度和热应力失效率的一种方法。例如，对于半径5nm的锡-银合金颗粒，可使其熔点从222℃降到193℃^[43]。