预测硅和无定形纳米材料性能的应用

众所周知，纳米结构的力学特性与大块结构的力学特性很不一样^[53]。但是，由于纳米实验技术和方法的限制，很难直接测量纳米结构的力学特性。作为另一种获得纳米结构力学特性的手段，分子动力学方法常用来描述纳米材料的物理响应，而这里用它来预测机械刚度。

采用附加了能量最小化程序模块的分子动力学方法来对纳米尺度样品进行模拟。根据弹性理论中的小变形假设^[54]，纳米材料的纵向延伸率应该小于1.0%。而且，依据圣维南（st.Venant）定律可知，需要一个纵横比较高的模型来防止边界效应，如图4.22所示。载荷和边界条件都在纵向加载。

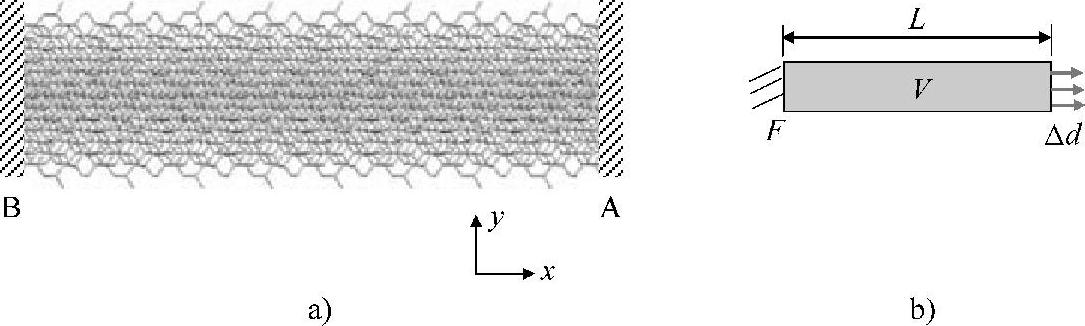
图4.22 硅棒模型及其载荷、边界条件的说明

a）模型 b）载荷、边界条件

固定端的作用力F_i（i代表第i个子步）可以由总能量梯度得到

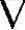U_fⁱ_{ixed end}＝F_xⁱi+F_yⁱj+F_zⁱk＝F_i （4.13）

式中，i、j和k代表三个正交矢量。

按照线弹性理论（Linear elasticity theory）^[54]，一维棒的力学变形可以写为Δd＝FL/EA。其中，F、E、L和A分别代表外部力、杨氏模量、长度和样品的横截面积。因而，可以得到杨氏模量为

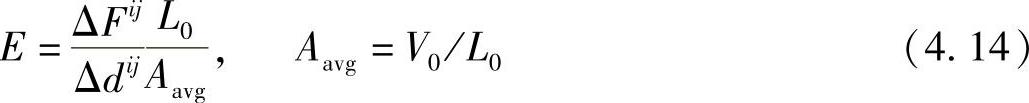
式中，ΔF^ij＝F^j-Fⁱ，j>i；Δd^ij＝d^j-dⁱ，j>i；V₀和L₀分别是初始体积和初始长度。

这个方法已经用来计算硅分子的性质，这个模型含有2688个硅原子，体积为58.3nm³。杨氏模量的计算值为130GPa，密度可以根据原子质量和分子体积的比值来求解，为2.5g/cm³。

对于无定型材料或多孔材料，当分子的化学结构生成以后，也可以使用上述方法。目前，有一些方法可以用来预测化学结构；其中一种方法是模拟无定型材料的整个制备过程；另一种方法是依据所测的化学信息生成一个类似的结构，这个方法有如下几个步骤：(www.xing528.com)

1）假设材料由几种结构单元组成。

2）通过实验方法（如核磁共振）得到每种结构单元之间的比例。

3）按照实验得到的分布比例把结构单元放置到预先定义的框架中。

4）采用几何优化方法来优化无定形分子的拓扑结构，进而得到无定形分子的近似模型。

采用上述方法能获得无定型材料SiOC（H）的近似模型。随着先进集成电路的特征尺寸持续减小，半导体工业正努力在技术上最小化信号传播过程的固有时间迟延，这一时间延迟可通过阻容延时来量化。对集成电路布线性能要求的提高，推动了铜线取代铝线，同时也促使人们开发出一种低介电常数材料来代替SiO₂薄膜^[4，55]。SiOC（H），也被称为黑钻石，由于其加工过程与现有的IC制造过程非常兼容而备受工业界的青睐。从黑钻石的化学结构看（见图4.23a），可以确定黑钻石的四种结构单元，如图4.23b所示。由于黑钻石是通过修改SiO₂得来的，因此这个框架只是假设。空穴的尺寸与一个结构单元类似，这已经由实验所证实。根据核磁共振的结果^[55]可知，基本结构Q、T、D、M和空穴在二氧化硅框架中分别按照20%、50%、18%、2%和10%的比率分布。

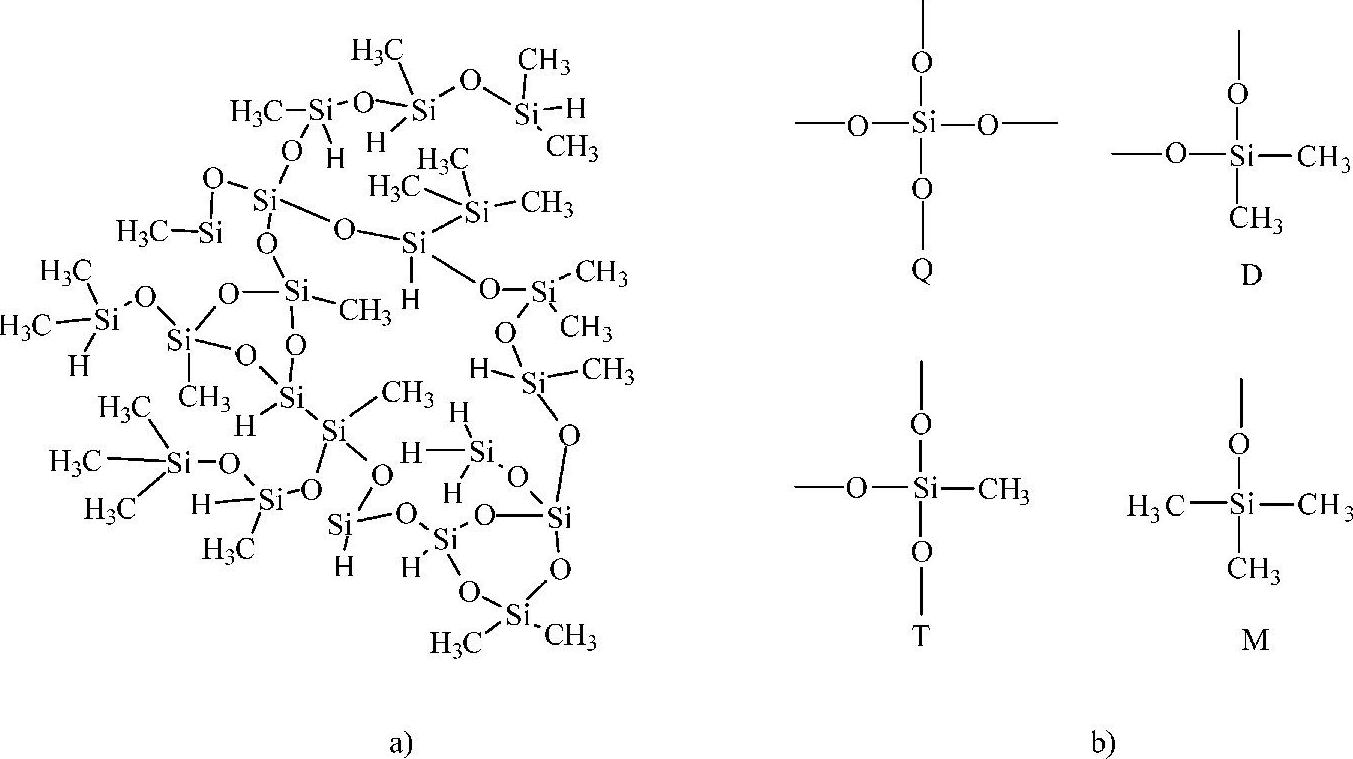
图4.23 黑钻石SiOC（H）的化学结构和结构单元

a）化学结构 b）Q、D、T和M结构单元

据此，可以得到黑钻石的分子拓扑结构，如图4.24a所示。因此，在对其进行几何优化之后，获得了无定形黑钻石的一个近似立体化学结构（即理想拓扑结构），如图4.24b所示。图4.24c给出了用分子动力学计算得到的、每个结构单元在黑钻石的整个杨氏模量上的敏感性。

图4.24 黑钻石SiOC（H）的模型

a）黑钻石的拓扑结构 b）理想拓扑结构 c）Q、T、D结构单元和空穴的敏感性计算值