分子动力学基础入门

从量子力学的角度看，物质有两种属性：颗粒性和波动性。但是，当系统的几何尺寸足够大时，单个元件的波动性并不明显，系统也就可以明确地确定。当忽略元件的波动性，或者通过势函数间接地考虑元件的波动性时，分子动力学方法就能高效地对分子系统进行模拟。分子动力学已在有机化学中广泛使用，它提供了一个框架来解决多颗粒问题[44]。分子动力学方法假设原子是刚性颗粒，其运动和颗粒之间的互相作用可以分别用坐标变量和势函数（或力场）来描述。图4.20给出了分子动力学的一种典型力学模型。

分子动力学的基本思想是，对于由N个颗粒构成的系统中每个颗粒i，依据牛顿运动第二定律有

F_i＝m_ia_i （4.10）

式中，m_i为颗粒i的质量；a_i＝d²r_i/dt²为其加速度；F_i为作用在颗粒上的力。

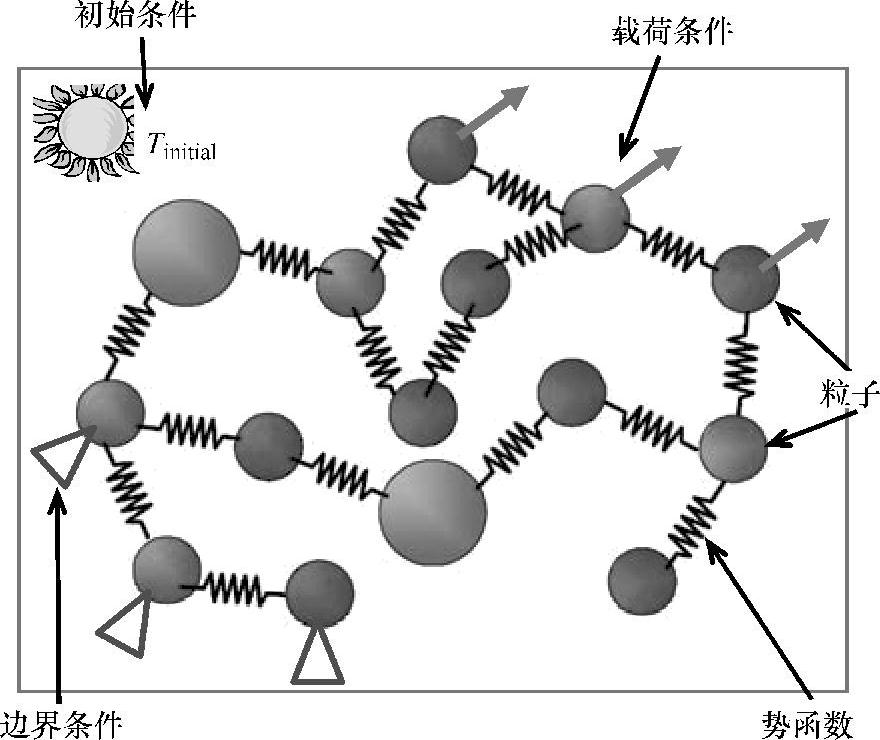
图4.20 分子动力学的力学模型

因此，分子动力学是一个确定性的方法：给定颗粒系统的一组初始位置和速度，就可以确定颗粒系统在后续时间内的演化过程。式（4.10）中颗粒间的相互作用力可以通过势函数或者力场来定义，有

式中，U为势函数；r_k为原子的坐标，k＝1，…，N。势函数可大致分如下几类：①对势函数；②经验多体势函数；③量子力学势函数。双体势函数，比如Lennard-Jones势函数U（r）＝4ε[（σ/r）12-（σ/r）6]（ε为最小能量对应的位置，σ为能量等于0时的距离^[45]）和Morse势函数U（r）＝D{exp[-α（r-r₀）]-1}²（r₀为平衡距离；α为弹性模量；D为粘附能^[46]）。Morse势函数多用来进行对计算效率要求较高的大型模拟。图4.21所示为一种典型的双体势函数。当双体系统的距离超过平衡距离（由r₀表示）时，根据库仑定律，引力能起主要作用。也就是说，随着距离逐渐增加，引力能逐渐减小，且当距离达到无限远的时候，引力能减小为0。相反地，当双体系统的距离减小时，引力能又变小，根据Pauli（泡利）排斥定律，斥力能增加。当距离接近0时，斥力能将无穷大。(https://www.xing528.com)

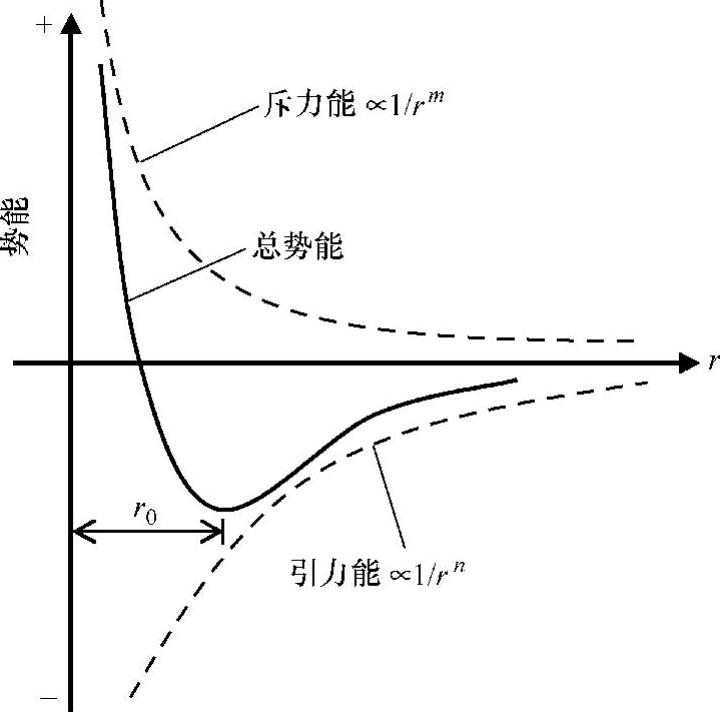
图4.21 双体势函数

对于多体系统而言，多体间的相互作用十分重要，常用的势函数有Stillinger_- Weber势函数^[47]、Tersoff势函数^[48]和Brenner势函数。这些势函数都是参数化的经验公式，它们含有的参数或者是通过对实验测量结果拟合得到，或者是通过对量子力学计算结果拟合得到。但是，当多体体统的坐标值和键合关系较大地偏离参数化的坐标值和键合关系时，这些势函数就会超出其适用范围，并导致产生不可靠的结果。正因为如此，人们加快了研究步伐，以便直接依据量子力学定律推导出原子间的相互作用。

式（4.10）表示的是特定时刻t时的系统状态。为了理解颗粒间的相互作用和力学响应，需要考虑时间积分。其中最常用的是基于有限差分方法的时间积分算法。分子动力学中两个主要的积分方法是蛙跳法和预估-校正方法^[49，50]。积分的时间步长必须小到可以捕捉到系统中振动模式的动力学特性，其振动模式的频率在10¹³/s量级。分子动力学描述的每个颗粒都有三个自由度，这些颗粒可以是固定颗粒也可以是自由颗粒。对于有十几亿个颗粒的系统，常采用周期性边界条件（Periodic Boundary Conditions，PBC）^[44]来减小计算量。

分子动力学模拟的初始条件包括定义系统中颗粒的初始坐标和速度，坐标可以通过实验或第一原理计算方法从计量化学得到，初始速度可由温度确定。根据均分公式K＝1.5Nk_BT（N为系统的颗粒数，k_B是玻耳兹曼常数），可知温度与动能直接相关。系统中每个颗粒的总动能遵循均分公式。而且，如果系统是静止的，质心的速度等于给定的系统速度或者为零。

原则上，分子动力学的理论基础是经典力学，分子动力学只是通过经典力学来描述原子间的相互作用。通常在忽略颗粒波动性或者间接考虑了颗粒波动性时，就能应用分子动力学。德布罗意热波长（De Broglie Thermal Wavelength）可用来验证系统应用这个经典假设的可信度，其中波长计算公式为

式中，M为原子质量；h为普朗克常数。如果Λ远小于a（a为系统中靠地最近的两个颗粒之间的距离），就说明满足经典方法的假设。然而，对于非常轻的系统（比如H₂、He、Li）或者温度足够低的系统，这个标准就不再满足了，因此量子效应就变得很重要而不能被忽略。因此，分子动力学不适合来模拟这些系统。