柔性电子脱层原因分析与粘着区域应用

图4.12a所示为柔性电子器件经常遇到的一种失效形式，即由于薄膜（比如ITO或SiN_x）和另外一个功能性层或衬底（如BCB、PI）之间出现了翘曲导致的脱层，如参考文献[34]所述的一样（见图4.12b）。在薄膜和衬底之间附着不良的初始区域中，压缩应力会导致薄膜屈曲。进一步地，翘曲产生的载荷会导致脱层区域开始扩展。这种失效的原因是屈曲和界面脱层的耦合作用^[7]。在过去的20年里，人们对固体薄膜的失效特性进行了大量研究工作，具体例子请参阅参考文献[7，35-37]。

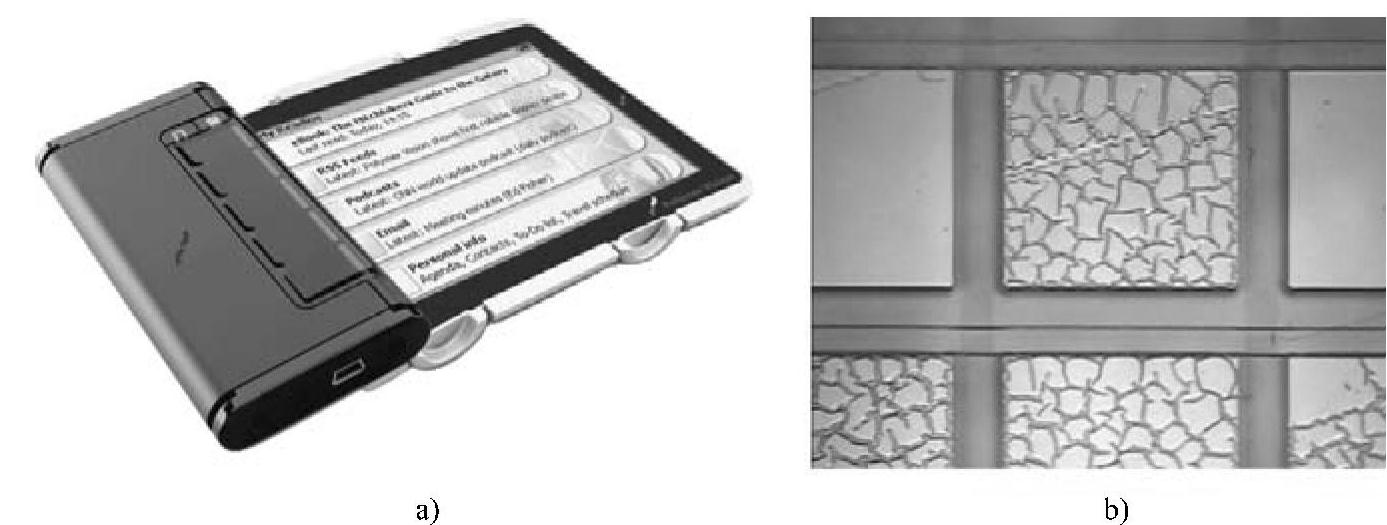
图4.12 自聚合物柔性显示器和采用像素观察到的翘曲引起的脱层

a）自聚合物柔性显示器（http：//www.polymervision.com授权） b）采用像素观察到的翘曲引起的脱层^[34]（已授权）

柔性样品的典型尺寸：薄膜厚度在100～800nm范围内，而衬底的厚度在100～500μm。为了实现全功能的柔性显示器（事实上，这是欧盟项目Flexidis的目标^[38]），我们应该了解和避免这些形式的失效。为此，人们发明了界面表征法和数值工具。

因为使用的材料都很薄，所以不能采用现有的标准实验方法（如剥离测试）来研究其失效模式。因此，Bouten^[34]和Abdallah等人^[35]设计了一套两点弯曲装置，如图4.13a所示。结果表明，可把翘曲的形态当作给定应变的函数进行研究，如图4.13b、c所示。通过增加曲率，样品的压缩应变也随之增加，在某些情况下弯曲的形态会由“直线”转变成“电话线”形态。

图4.13 Bouten和Abdallah等人针对柔性电子产品提出的力学两点弯曲装置，以及“直线”和“电话线”翘曲形态的共焦显微镜图像（从图b到图c的 弯曲应变是增加的）（图片由A.Abdallah和C.van Rekum提供）

a）力学两点弯曲装置 b）“直线” c）“电话线”

基于Hutchinson和Suo^[7]提出的模型，可采用近似的解析解来估算界面强度值。但是，这些分析模型内含的假设（例如层的数量和弹性材料的性质）限制了它们的适用范围。因此，人们已经提出了不受这些限制的数值模型^[39]。图4.14所示为一个二维两层系统。事实上，这个模型是多层系统中压缩区域的一个局部模型。这个模型采用上述提到的内聚区单元来对界面失效的初始和扩展过程进行建模。为了触发翘曲，在这个模型中插入了一个初始几何缺陷。为了验证这个数值模型，参考文献^[39]模拟了一个基准问题，结果发现这个数值模型精确地捕捉了翘曲导致的脱层行为。

通过比较计算翘曲几何形状与翘曲高度（w）和宽度（2b）的实验测量值，这种模型将被用来评估薄膜层中分离和残余应变的界面行为。正如上面所述，本实验所用的装置是图4.13a所示的两点弯曲测试装置。目前，只能在样品校直后测量其翘曲的几何特性，而不能在加载中或加载后对样品进行翘曲几何的精确测量。因此，在模拟过程中应考虑之前经过对材料的影响，因为这些决定了样品在加载和卸载时的表现，可分别参阅参考文献[36，21]来对衬底的塑性和内聚区的不可逆性进行建模。更要注意的是，整个模拟过程均假定薄膜层发生弹性变形。(www.xing528.com)

图4.15给出了在t_max＝100MPa时加载状态和校直后薄膜的翘曲几何形状，以便说明加载和后续校直对薄膜翘曲的影响。可以观察到，校直的结果是翘曲高度显著减小；而且因为脱层区域前端塑性区的大小由衬底、ITO层和内聚区等决定，产生的最大牵引力t_max也会在一定情况下影响结果；并且最大牵引力t_max越大，通过内聚区和小翘曲宽度而传播的应力更大，导致衬底中的塑性应变值也相应增大。对于t_max＝100MPa，最大的塑性应变是7.5%；而对于t_max＝200MPa，最大的塑性应变是32%。

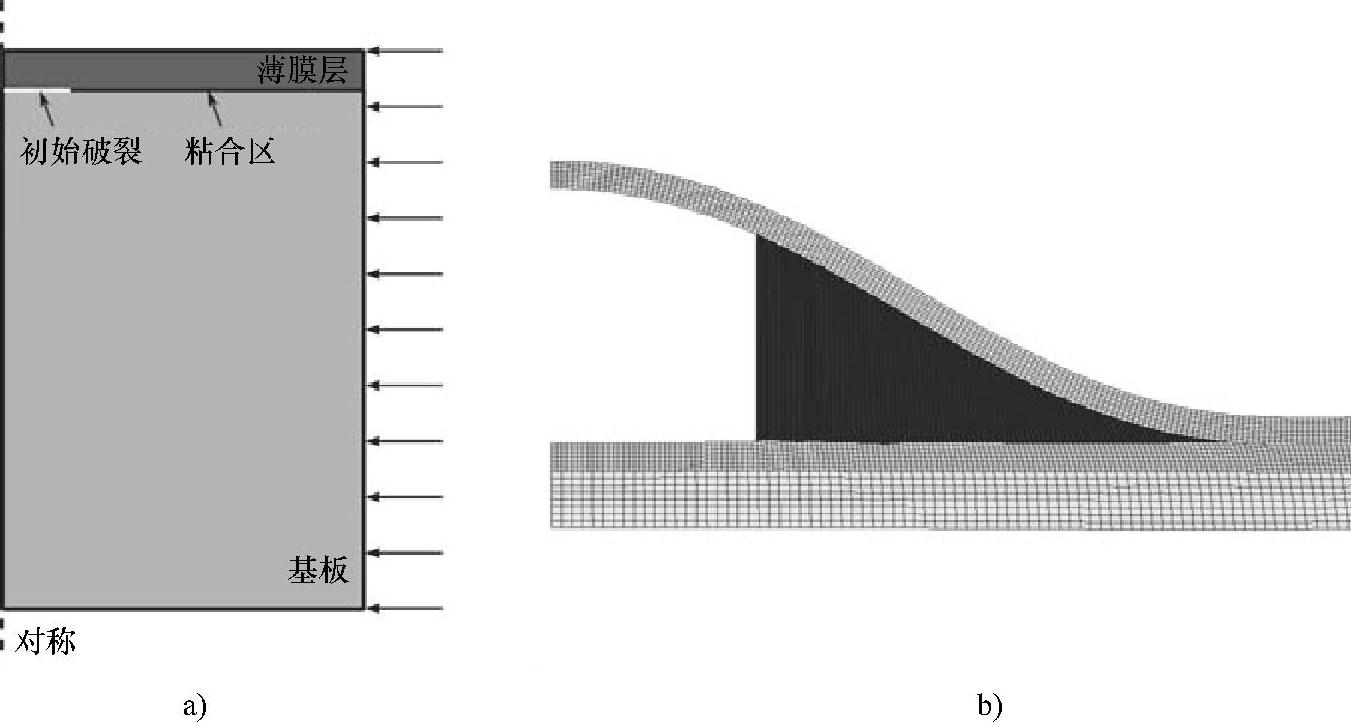
图4.14 二维两层系统的模型及形变（这个云图表明粘着区域元素的损害值：对应一个裂纹的损害值为1.00）

a）二维翘曲脱层模型 b）包括脱层区域的放大的变形几何

图4.15 加载状态和校直状态下的翘曲几何

经实验测得，该翘曲的宽度2b＝3.3μm、高度w＝0.14μm。同数值模拟的结果相比，分离力所做的功和总的压缩应变值分别为G＝37J/m²和1.82%（对应t_max＝100MPa）。上述结果都是在初始缺陷长度为2b₀＝2μm的情况下得到的。所以考虑到材料的历史依赖性及其加载校直条件，该实验-数值方法能用来分析分离薄膜结构的界面所需要的功。

接下来的工作集中在下列方向：

1）解释从“直线”到“电话线”翘曲的转变现象，Abdallah等人^[35]（见图4.13）已经对此作了相关的报告。为了实现这个设想，与Jensen和Sheinman^[40]相似，需要发展数值模型，从基于模式角和压缩应力的角度来考虑界面韧度的影响。此外，增加的压缩应力也被推断为转变的主要驱动力（如参考文献^[35，40]）。

2）延续Hutchinson^[41]和Moo等人^[42]的工作，研究柔性多层系统中初始缺陷的几何特征（比如形状和尺寸）对翘曲导致的脱层行为的影响。